この記事は4部構成のシリーズ「回転に関する物理量」の第2部になっています。第2部では、力のモーメントに関連する物理量である角速度 $\boldsymbol{\omega}$ を多くのサイトではなぜか疎かにされる定義から紹介していきます。第3部以降では角速度から角運動量や慣性モーメントを定義していきます。
式番号は前回からの引き継ぎ。
ベクトルとしての角速度 $\boldsymbol{\omega}$
角速度 $\boldsymbol{\omega}$ とはベクトル量であり、その大きさは高校物理で取り上げられるものとなる。しかし高校物理では角速度がベクトル量であることを伝えていない。実は高校物理で言われる角速度 $ω$ とは角振動数（又は角周波数）であり、角速度 $\boldsymbol{\omega}$ とは明確に区別されていることに注意されたい。
さてなぜかよく分からないが、どこのサイトに寄っても角速度 $\boldsymbol{\omega}$ が
$$\boldsymbol{\omega}:=ω\boldsymbol{e}_ω=\frac{|\boldsymbol{v}|}{|\boldsymbol{r}|} \frac{\boldsymbol{r}×\boldsymbol{v}}{|\boldsymbol{r}×\boldsymbol{v}|} \tag{6}$$
のように定義されるとしか書かれていない。ただ角速度 $\boldsymbol{\omega}$ の大きさに方向を付け足しただけである。これでは円運動のときでしか成り立たない（のに恰もこれが本来の定義であるかのように言う）し、なぜそのように定義したのかよく分からないのではないか。
ここでは角速度 $\boldsymbol{\omega}$ がどのようにして定義されたのか見ていこうと思う。
まず右図に示すような微小三角形OABの面要素 $d\boldsymbol{S}$ を考えてみる。この三角形の面積は
$$dS=\frac{1}{2} |\boldsymbol{r}_{(t)}||\boldsymbol{r}_{(t+dt)}|\sinθ_{(t+dt)}=\frac{1}{2}|\boldsymbol{r}_{(t)}×\boldsymbol{r}_{(t+dt)}| \tag{7}$$
となる。よって微小三角形OABの面要素 $d\boldsymbol{S}$ は外積の向きを考慮して
$$d\boldsymbol{S}=\frac{1}{2}\boldsymbol{r}_{(t)}×\boldsymbol{r}_{(t+dt)} \tag{8}$$
と表される。この外積の向きこそが角速度 $\boldsymbol{\omega}$ の向きとなる。
外積についてはこちらの記事
を確認されたい。
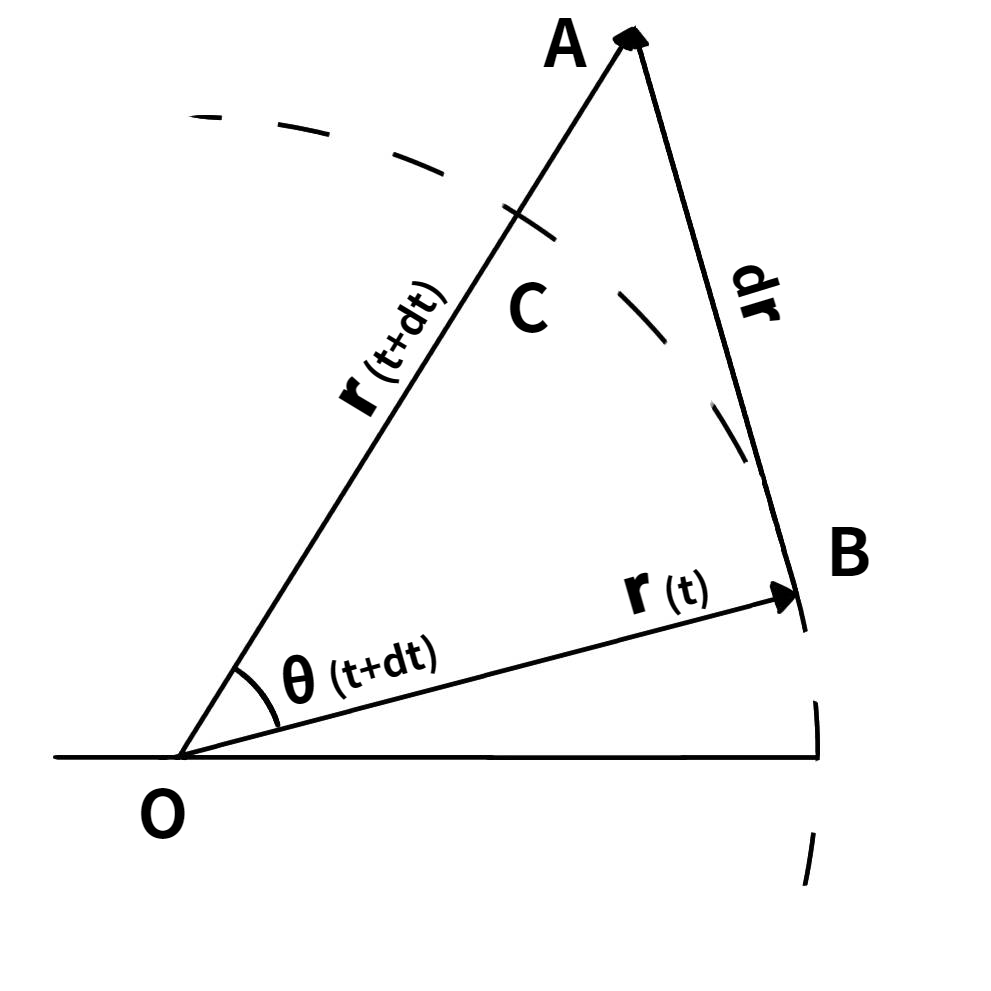
ここで扇形OBCの面積は
$$\frac{1}{2} |\boldsymbol{r}_{(t)}||\boldsymbol{r}_{(t)}|θ_{(t+dt)} \tag{9}$$
と表されるが、特に $dt→0$ のときには1次近似により $θ_{(t+dt)}≈\sinθ_{(t+dt)}$ となるので
$$\begin{align*}
\lim_{dt→0} \frac{1}{2} |\boldsymbol{r}_{(t)}||\boldsymbol{r}_{(t+dt)}|θ_{(t+dt)}&=\frac{1}{2} |\boldsymbol{r}_{(t)}||\boldsymbol{r}_{(t)}|\lim_{dt→0}\sinθ_{(t+dt)}\\
&=\lim_{dt→0} dS=\frac{1}{2}|\boldsymbol{r}_{(t)}×\lim_{dt→0}\boldsymbol{r}_{(t+dt)}|
\end{align*}$$
となる。このことから扇形OBCと三角形OABは微小極限で等しくなることが分かる。よって両辺を $t$ で微分するということは
$$\frac{1}{2} |\boldsymbol{r}_{(t)}||\boldsymbol{r}_{(t)}|\lim_{dt→0}\frac{θ_{(t+dt)}}{dt}=\lim_{dt→0} \frac{dS}{dt}=\frac{1}{2}\left|\boldsymbol{r}_{(t)}×\lim_{dt→0}\frac{\boldsymbol{r}_{(t+dt)}}{dt}\right|$$
$$∴\frac{1}{2} |\boldsymbol{r}_{(t)}||\boldsymbol{r}_{(t)}|ω=\frac{1}{2}|\boldsymbol{r}_{(t)}×\boldsymbol{v}_{(t)}|$$
ということである。これは扇形OBCと三角形OABの面積速度が等しいことを意味する。よって角速度ベクトル $\boldsymbol{\omega}$ は外積の向きを考慮して
$$\boldsymbol{\omega}:=\frac{1}{|\boldsymbol{r}_{(t)}|^2} \boldsymbol{r}_{(t)}×\boldsymbol{v}_{(t)}=\frac{1}{r^2} \boldsymbol{r}×\boldsymbol{v} \tag{10}$$
と定義すれば、角速度 $\boldsymbol{\omega}$ は規格化された1つの回転律として扱うことができる。
角速度 $\boldsymbol{\omega}$ を用いて角運動量 $\boldsymbol{L}$ を表現
$\boldsymbol{\omega}×\boldsymbol{r}$ は
$$\begin{align*}
\boldsymbol{\omega}×\boldsymbol{r}&=(\frac{1}{r^2} \boldsymbol{r}×\boldsymbol{v})×\boldsymbol{r}\\
&=\frac{1}{r^2}( (\boldsymbol{r}\cdot\boldsymbol{r})\boldsymbol{v}-(\boldsymbol{v}\cdot\boldsymbol{r})\boldsymbol{r})\\
&=\boldsymbol{v}-\frac{\boldsymbol{r}}{r^2}(\boldsymbol{r}\cdot\boldsymbol{v})\\
&=\boldsymbol{v}-\frac{(\boldsymbol{r}\cdot\boldsymbol{v})}{r}\frac{\boldsymbol{r}}{r}\\
&=\boldsymbol{v}-v_r\boldsymbol{e}_r
\end{align*} \tag{11}$$
となる。最後の第2項は正射影ベクトルと呼ばれるもので、 $v_r$ とは速度 $\boldsymbol{v}$ が半径 $r$ 方向に関与している大きさを表し、 $\boldsymbol{e}_{r_{(θ)}}$ を半径 $r$ 方向の基底とした。つまり極端な話が速度 $\boldsymbol{v}$ が半径 $r$ 方向の基底 $\boldsymbol{e}_{r_{(θ)}}$ による単一の線型結合で表される場合には $\boldsymbol{v}-v_r\boldsymbol{e}_r=0$ となり、物体は回転しない。これは(10)式からも分かる。又速度 $\boldsymbol{v}$ が半径 $r$ 方向の基底 $\boldsymbol{e}_{r_{(θ)}}$ と線型独立であるのならば(11)式は
$$\boldsymbol{\omega}×\boldsymbol{r}=\boldsymbol{v} \tag{12}$$
となる。よって物体が円運動するときには(4)式
$$\boldsymbol{L}=\boldsymbol{r}×\boldsymbol{p}=\boldsymbol{r}×m\boldsymbol{v} \tag{4}$$
は(11)式を用いて
$$\begin{align*}
\boldsymbol{L}&=\boldsymbol{r}×\boldsymbol{p}=\boldsymbol{r}×m\boldsymbol{v}\\
&=\boldsymbol{r}×m(\boldsymbol{\omega}×\boldsymbol{r}+v_r\boldsymbol{e}_r)\\
&=m(\boldsymbol{r}×(\boldsymbol{\omega}×\boldsymbol{r}+v_r\boldsymbol{e}_r))\\
&=m((\boldsymbol{r}\cdot\boldsymbol{r})\boldsymbol{\omega}-(\boldsymbol{r}\cdot\boldsymbol{\omega})\boldsymbol{r}+v_r\boldsymbol{r}×\boldsymbol{e}_r)\\
&=m(r^2\boldsymbol{\omega}-(\boldsymbol{r}\cdot\boldsymbol{\omega})\boldsymbol{r})
\end{align*} \tag{13}$$
となる。途中 $\boldsymbol{r}×\boldsymbol{e}_r=0$ であるから、円運動の場合の角速度
$$\boldsymbol{\omega}×\boldsymbol{r}=\boldsymbol{v} \tag{12}$$
を用いても同様の結果を得る。
しかし1つ疑問に思うところがあることだろう。その通りである。(4)式
$$\boldsymbol{L}=\boldsymbol{r}×\boldsymbol{p}=\boldsymbol{r}×m\boldsymbol{v} \tag{4}$$
は角速度
$$\boldsymbol{\omega}=\frac{1}{|\boldsymbol{r}_{(t)}|^2} \boldsymbol{r}_{(t)}×\boldsymbol{v}_{(t)}=\frac{1}{r^2} \boldsymbol{r}×\boldsymbol{v} \tag{10}$$
を用いて
$$\boldsymbol{L}=\boldsymbol{r}×\boldsymbol{p}=\boldsymbol{r}×m\boldsymbol{v}=mr^2\boldsymbol{\omega} \tag{13亜}$$
となるが、この式と(13)式
$$\boldsymbol{L}=m(r^2\boldsymbol{\omega}-(\boldsymbol{r}\cdot\boldsymbol{\omega})\boldsymbol{r}) \tag{13}$$
を比較したときに、(13)式は余計な第2項がくっ付いているではないかという主張であろう。
これは(13)式、(13亜)式で使われる半径 $r$ が指しているものが異なることが原因である。
角運動量 $\boldsymbol{L}$ を表現するために、(13亜)式では
$$\boldsymbol{\omega}=\frac{1}{r^2} \boldsymbol{r}×\boldsymbol{v} \tag{10}$$
を使用したが、(13)式では
$$\boldsymbol{\omega}×\boldsymbol{r}=\boldsymbol{v}-v_r\boldsymbol{e}_r \tag{11}$$
を使用した。
(10)式では外積の定義から角速度 $\boldsymbol{\omega}$ は位置ベクトル $\boldsymbol{r}$ と速度 $\boldsymbol{v}$ に垂直なベクトルとなる。つまり位置ベクトル $\boldsymbol{r}$ と速度 $\boldsymbol{v}$ が同一平面上でのベクトルなのに対し、これへ垂直に貫くように角速度 $\boldsymbol{\omega}$ が設定される。そのためこの角速度 $\boldsymbol{\omega}$ は回転軸と言われる。
一方で(11)式でも外積が使われているが、これでは角速度 $\boldsymbol{\omega}$ が位置ベクトル $\boldsymbol{r}$ と速度 $\boldsymbol{v}$ に垂直なベクトルであるかは分からない。そのため
$$\boldsymbol{L}=\boldsymbol{I}\boldsymbol{\omega} \tag{14}$$
のように角運動量 $\boldsymbol{L}$ を角速度 $\boldsymbol{\omega}$ による$\boldsymbol{I}$ の線形変換で表したいときに、一般に回転軸が固定されていない場合には、軸のブレを修正するための項が必要になってくるのである。
例えば $xy$ 平面に平行な面で円運動をする位置ベクトル $\boldsymbol{r}=x\boldsymbol{e}_x+y\boldsymbol{e}_y+z\boldsymbol{e}_z$ の質点について(14)式のように $\boldsymbol{\omega}$ で表現されるとすれば、角運動量は(13)式より
$$\begin{align*}
\boldsymbol{L}&=m(r^2\boldsymbol{\omega}-(\boldsymbol{r}\cdot\boldsymbol{\omega})\boldsymbol{r}) \tag{13}\\
&=m\left((x^2+y^2+z^2)\boldsymbol{\omega}-(\boldsymbol{r}\cdot\boldsymbol{\omega})\frac{(\boldsymbol{r}\cdot\boldsymbol{\omega})}{|\boldsymbol{r}\times\boldsymbol{v}|}(\boldsymbol{r}\times\boldsymbol{v})\right)\\
&=m\left((x^2+y^2+z^2)\boldsymbol{\omega}-(r\cosθ)^2 ω\boldsymbol{e}_z\right)\\
&=m\left((x^2+y^2+z^2)\boldsymbol{\omega}-(r\cosθ)^2 \boldsymbol{\omega}\right)
\end{align*} \tag{15}$$
となる。ただし $θ$ は球座標系 $(r,θ,φ)$ における位置ベクトル $\boldsymbol{r}$ の $z$ 軸との偏角を表す。右辺第1式第2項は $\boldsymbol{\omega}$ によって正射影した。よって球座標系において $z=r\cosθ$ と表されることから、(15)式から角運動量は
$$\boldsymbol{L}=m(x^2+y^2)\boldsymbol{\omega}$$
となる。当然これは回転軸を固定した場合における角運動量 $\boldsymbol{L}$
$$\boldsymbol{L}=mr^2\boldsymbol{\omega} \tag{13亜}$$
と一致する。ただし(13亜)式の半径 $r$ は $xy$ 平面での円運動の半径 $r^2=x^2+y^2$ である。
ちょっと休憩
高校物理では角速度を習ったが、これは実は円運動における角周波数 $ω$ のことを指し、一般的には角速度と言えばベクトル $\boldsymbol{\omega}$ で表される量のことである。次回以降は次回では角運動量 $\boldsymbol{L}$ と角速度 $\boldsymbol{\omega}$ の関係式から導かれる慣性モーメントテンソル $\boldsymbol{I}$ について紹介する。ただし剛体の運動を解明しようとしていて明らかに高校物理の範囲外になるので、サラっと流してもらって構わない。
コメント