高校数学では内積を習ったが、なせか外積は教科書で全く触れられていなかった。そのため高校物理などでは特に苦労した生徒がいたことだろう。愚直に左手を振り回す姿は滑稽に映る。この記事ではベクトルの外積を多角的な視点から定義しよう。
また次回の記事
では複素ベクトルの外積を独自に定義してみようと思う。自然な形で複素ベクトルに拡張すると案外計算が上手く行くことが分かってもらえれば嬉しい。定義の妥当性はそれなりに保障されていると自負している。
内積と表裏一体の外積
内積とは2つのベクトルの従属度合いによる量であった。従属度合いが強ければ強いほど内積は大きくなり、このことから内積は2つのベクトルが同一のただ1つの基底 $e$ によって
$$\boldsymbol{x}=A\boldsymbol{e} \boldsymbol{y}=B\boldsymbol{e}$$
のように同型写像されるときに最大の大きさとなる。このとき $A,B$ は単なるスカラーであり、内積は
$$\boldsymbol{x}\cdot\boldsymbol{y}=AB$$
となる。逆に各ベクトルの基底が線型独立であるのならば、これは従属度合いが常に $0$ ということである。
内積について詳しく知りたい読者はこちらを参考にされたい。
これを聞いて、逆に独立度合いに依存する量も考えてみたいところであろう。こちらは内積とは対称的に外積と呼ばれる。まあ焦らずにまずは復習がてら内積をちょっと変わった視点から考えてみよう。
線型写像としての内積
まず $n$ 次元ベクトル $\boldsymbol{x}$ について作用素 $\boldsymbol{A}$ による $m$ 次元ベクトル $\boldsymbol{y}$ への線型写像
$$\boldsymbol{y}=\boldsymbol{A}\boldsymbol{x} \tag{1}$$
を考えてみる。このとき作用素 $\boldsymbol{A}$ は2階のテンソル $A_{ij}$ で表されるが、特に $i=1$ に固定した $1$ 階のテンソル $A_j$ とは $n$ 次元行ベクトルの $j$ 成分を表す。よって(1)式をテンソル表記すると、
$$y_1=\sum_jA_jx_j \tag{2}$$
となる。このことから(2)式は $\mathbb{K}^n→\mathbb{K}^1$ の線型写像となっている。
線型写像についてもう少し知りたい方はこちらの記事
を参考にされたい。
よって(2)式はベクトル $\boldsymbol{A}$ を実ベクトルとしたときに2つのベクトル $\boldsymbol{A},\boldsymbol{x}$ の内積
$$\begin{align*}\boldsymbol{A}\cdot\boldsymbol{x}&=\begin{pmatrix}A_1 & A_2 & \cdots & A_n \end{pmatrix}
\begin{pmatrix}x_1 \\ x_2 \\ \vdots \\ x_n\end{pmatrix}\\
∴ y_1&=\sum_jA_jx_j\end{align*}$$
として表される。よって内積の計算結果がスカラーとなるのは(2)式の $\boldsymbol{y}$ が1次元の数ベクトルとなることからも明らかである。そこで敢えて1次元の幾何ベクトルとして方向を定めるのなら、内積の従属度合いに依存した量という意味から2つのベクトル $\boldsymbol{A},\boldsymbol{x}$ の基底のどちらかを選択しても良さそうである。
外積を定義してみる
さて実ベクトル $\boldsymbol{x},\boldsymbol{y}$ の内積 $\boldsymbol{x}\cdot\boldsymbol{y}$ は幾何学的な解釈
$$\boldsymbol{x}\cdot\boldsymbol{y}=|\boldsymbol{x}||\boldsymbol{y}|\cosθ \tag{3}$$
によって定義することもできた。ここで簡単のため2つの実ベクトル $\boldsymbol{x},\boldsymbol{y}$ を $xy$ 平面の2次元ベクトルとし、各成分を
$$\boldsymbol{x}=\begin{pmatrix}X \\ Y\end{pmatrix} \boldsymbol{y}=\begin{pmatrix}x \\ y\end{pmatrix}$$
と置く。このとき $\cosθ$ について解くと、内積の定義と(3)式より
$$\begin{align*}
Xx+Yy&=\sqrt{X^2+Y^2}\sqrt{x^2+y^2}\cosθ\\
∴ \cosθ&=\frac{Xx+Yy}{\sqrt{X^2+Y^2}\sqrt{x^2+y^2}}
\end{align*}$$
となる。
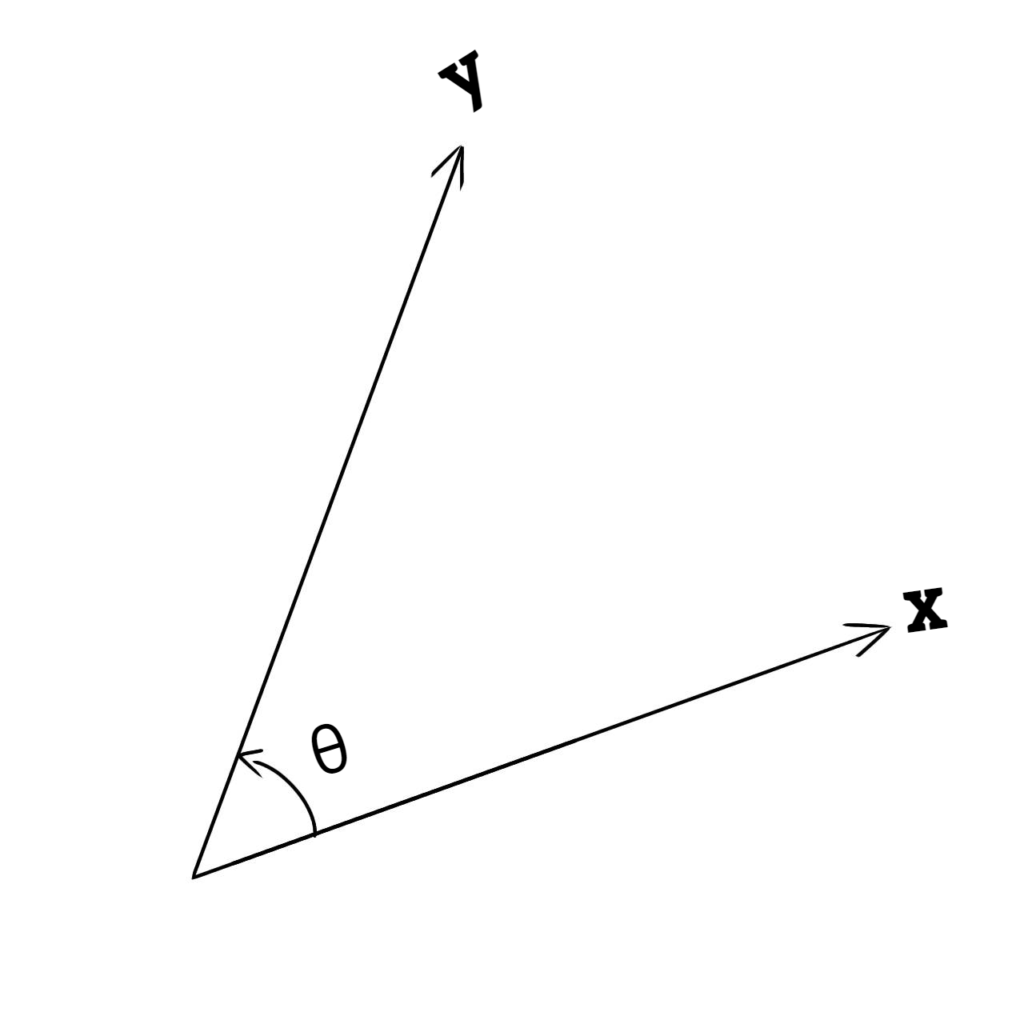
よって $\sinθ$ は
$$\begin{align*}
\sinθ&=±\frac{\sqrt{(X^2+Y^2)(x^2+y^2)-(Xx+Yy)^2}}{\sqrt{X^2+Y^2}\sqrt{x^2+y^2}}\\
&=±\frac{\sqrt{X^2y^2+Y^2x^2-2XxYy}}{\sqrt{X^2+Y^2}\sqrt{x^2+y^2}}\\
&=±\frac{\sqrt{(Xy-Yx)^2}}{\sqrt{X^2+Y^2}\sqrt{x^2+y^2}}\\
&=±\frac{Xy-Yx}{\sqrt{X^2+Y^2}\sqrt{x^2+y^2}}\\
&=±\frac{Xy-Yx}{|\boldsymbol{x}||\boldsymbol{y}|}
\end{align*} \tag{4}$$
となる。これにより(4)式の分子を
$$\boldsymbol{x}×\boldsymbol{y}\stackrel{?}{:=}Xy-Yx=|\boldsymbol{x}||\boldsymbol{y}|\sinθ$$
と置くことで2つのベクトル $\boldsymbol{x},\boldsymbol{y}$ の独立度合いに依存する量 $\boldsymbol{x}×\boldsymbol{y}$ が得られよう! ……と単純に終わってしまっては勿体無い。内積のときには敢えてこれを1次元幾何ベクトルと見なすのなら、内積は対象となる2つのベクトルのいずれかの方向のベクトルの掛け算となる。ところで外積とは対象となる2つのベクトルの独立度合いに依存することから、外積の向きは対象となる2つのベクトルに垂直なベクトルとなるのである。
このことから外積 $\boldsymbol{x}×\boldsymbol{y}$ は
大きさが $|\boldsymbol{x}||\boldsymbol{y}|\sinθ=Xy-Yx$ である向き $z$ 軸方向のベクトル $(\boldsymbol{x}×\boldsymbol{y})_z$ となる。
同様に2つのベクトル $\boldsymbol{x},\boldsymbol{y}$ が $yz$ 平面、 $zx$ 平面上にある場合には、それぞれ
$$\begin{align*}(\boldsymbol{x}×\boldsymbol{y})_x&=Yz-Zy\\
(\boldsymbol{x}×\boldsymbol{y})_y&=Zx-Xz\end{align*}$$
となる。よって3次元実空間の2つのベクトル
$$\boldsymbol{x}=\begin{pmatrix}X \\ Y \\ Z\end{pmatrix} \boldsymbol{y}=\begin{pmatrix}x \\ y \\ z\end{pmatrix}$$
の外積 $\boldsymbol{x}×\boldsymbol{y}$ について、一般の場合には
$$\boldsymbol{x}×\boldsymbol{y}=(Yz-Zy)\boldsymbol{e}_x+(Zx-Xz)\boldsymbol{e}_y+(Xy-Yx)\boldsymbol{e}_z \tag{5}$$
となる。(4)式は最も広く広まっている定義式ではあると思うが、これを
$$\begin{pmatrix}
0 & -Z & Y\\
Z & 0 & -X\\
-Y & X & 0
\end{pmatrix}
\begin{pmatrix}
x\\y\\z
\end{pmatrix} \tag{6}$$
や、或いは更にこれを変形した
$$\begin{align*}&=\begin{pmatrix}
\begin{pmatrix}
0 & 0 & 0\\
0 & 0 & Y\\
0 & -Z & 0
\end{pmatrix}_1
\begin{pmatrix}
0 & 0 & -X\\
0 & 0 & 0\\
Z & 0 & 0
\end{pmatrix}_2
\begin{pmatrix}
0 & X & 0\\
-Y & 0 & 0\\
0 & 0 & 0
\end{pmatrix}_3
\end{pmatrix}
\begin{pmatrix}
x\\y\\z
\end{pmatrix}\\
&= \begin{pmatrix}
\begin{pmatrix}
0 & 0 & 0\\
0 & 0 & 1\\
0 & -1 & 0
\end{pmatrix}_1
\begin{pmatrix}
0 & 0 & -1\\
0 & 0 & 0\\
1 & 0 & 0
\end{pmatrix}_2
\begin{pmatrix}
0 & 1 & 0\\
-1 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}_3
\end{pmatrix}
\begin{pmatrix}
\begin{pmatrix}
0 & 0 & 0 \\
0 & Z & 0 \\
0 & 0 & Y
\end{pmatrix}_1\\
\begin{pmatrix}
Z & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & X
\end{pmatrix}_2\\
\begin{pmatrix}
Y & 0 & 0 \\
0 & X & 0 \\
0 & 0 & 0
\end{pmatrix}_3
\end{pmatrix}
\begin{pmatrix}
x\\y\\z
\end{pmatrix}\\
&= \begin{pmatrix}
\begin{pmatrix}
0 & 0 & 0\\
0 & 0 & 1\\
0 & -1 & 0
\end{pmatrix}_1
\begin{pmatrix}
0 & 0 & -1\\
0 & 0 & 0\\
1 & 0 & 0
\end{pmatrix}_2
\begin{pmatrix}
0 & 1 & 0\\
-1 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}_3
\end{pmatrix}
\begin{pmatrix}
\begin{pmatrix}
0 \\
Zy \\
Yz
\end{pmatrix}_1\\
\begin{pmatrix}
Zx \\
0 \\
Xz
\end{pmatrix}_2\\
\begin{pmatrix}
Yx \\
Xy \\
0
\end{pmatrix}_3
\end{pmatrix}
\end{align*} \tag{7}$$
や、エディントンのイプシロン(レヴィ=チヴィタの記号)を $ε_{ijk}$ と置いた下でこれをテンソル表記した
$$ ε_{ij}^k(X_{i}x_j)_k\boldsymbol{e}_k \tag{8}$$
のように定義されることもある。
各定義の説明
線型変換としての外積
(6)式
$$\begin{pmatrix}
0 & -Z & Y\\
Z & 0 & -X\\
-Y & X & 0
\end{pmatrix}
\begin{pmatrix}
x\\y\\z
\end{pmatrix} \tag{6}$$
の定義は外積 $\boldsymbol{x}×\boldsymbol{y}$ を $\boldsymbol{y}$ の線型変換で表すというものである。そのときの線型変換 $f$ を表す表現行列 $\boldsymbol{A}$ は
$$\boldsymbol{A}=
\begin{pmatrix}
0 & -Z & Y\\
Z & 0 & -X\\
-Y & X & 0
\end{pmatrix} \tag{9}$$
となる。この定義の良さは外積を線型変換で表現することで簡潔に書き表されるところにある。例えば外積 $\boldsymbol{x}×\boldsymbol{y}$ をした後に左から内積を取ったもの $\boldsymbol{P}\cdot(\boldsymbol{x}×\boldsymbol{y})$ について、これは内積 $\boldsymbol{P}\cdot\boldsymbol{y}$ を $\boldsymbol{y}$ の線型写像 $g$ として表される表現行列 $\boldsymbol{B}$ (1階のテンソル)との合成写像 $g◦f$ を表す合成行列 $\boldsymbol{B}\boldsymbol{A}$ によって
$$\boldsymbol{B}\boldsymbol{A}\boldsymbol{y}$$
のように書くだけで済む。
行列階での表現
3階のテンソル $T_{ijk}\hspace{1mm}(i≤l,j≤m,k≤n)$ は幾何学的には各要素が直方体上に並べられた行列階 $(l×m×n)$ の各要素を表しているのである。
(7)式の途中では行列階の積を施している。1行目から2行目への変形は各階について行列の変数を分離させた。本来なら階は立体的に積み下げて並べられて計算されるものであるが、ここでは各階の行列を列ベクトルの内積ように並べることで(実際には階行列ベクトルであるが)計算した。2行目から3行目への変形は階を固定して各階の行列の積を施している。最後の
$$ε_{ijk}=\begin{pmatrix}
0 & 0 & 0\\
0 & 0 & 1\\
0 & -1 & 0
\end{pmatrix}_1
\begin{pmatrix}
0 & 0 & -1\\
0 & 0 & 0\\
1 & 0 & 0
\end{pmatrix}_2
\begin{pmatrix}
0 & 1 & 0\\
-1 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}_3 \tag{10}$$
とはレヴィチ・ヴィタの記号であり、 $(i,j,k)=(1,2,3)$ を基本順列として
$$ε_{ijk}=\begin{cases}+1 (偶順列)\\
-1 (奇順列)\\
0 (その他)
\end{cases}$$
となる。(8)式で添え字が $k$ だけ上付きなのは、(7)式の3行目が階 $k$ についての積の計算となっているからである。詳しくはアインシュタインの縮約記法を参照されたい。
外積で現れる反対称性について
さて(9)式
$$\boldsymbol{A}=
\begin{pmatrix}
0 & -Z & Y\\
Z & 0 & -X\\
-Y & X & 0
\end{pmatrix} \tag{9}$$
と(10)式
$$ε_{ijk}=\begin{pmatrix}
0 & 0 & 0\\
0 & 0 & 1\\
0 & -1 & 0
\end{pmatrix}_1
\begin{pmatrix}
0 & 0 & -1\\
0 & 0 & 0\\
1 & 0 & 0
\end{pmatrix}_2
\begin{pmatrix}
0 & 1 & 0\\
-1 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}_3 \tag{10}$$
はどちらも反対称的である。(9)式は反対称行列となり、(10)式は完全反対称テンソルとなる。レヴィ・チヴィタの記号 $ε_{ijk}$ について「完全」が添えられているのは、任意の添え字 $i,j,k$ についてこれらの取り替えを施しても「完全」に反対称性を満足するからである。このことはレヴィ・チヴィタの記号を行列階で表現したときに対角成分 $i=j=k$ を軸に反対称であることからも分かる。
ちょっと休憩
この記事では実ベクトルの外積を多角的な視点から定義してみた。ここでは3次元ベクトルのみを扱っているが、四元数などの超複素数による定義を用いれば高次元ベクトルにおける外積も定義できるので、いつか機会があれば紹介してみようと思う。ここでは複素ベクトルの内積と同じような感覚で複素ベクトルの外積を定義してみようというのが最終目的なので、次回ではここで定義した線型変換の考え方による外積を複素ベクトルに拡張してみようと思う。
次回



コメント