この記事は4部構成のシリーズ「期待値を図形的に解釈してみた」の第3部になります。これらの記事を通して楕円の方程式が示す意味や数学的背景を紹介していきます。第3部では規格化された期待値 $\langle r|\boldsymbol{A}|r\rangle=1$ で表される図形を詳しく調べていこうと思います。
式番号は前回の引き継ぎ。
初回
前回
次回
期待値から二次形式へ
二次形式の標準化
規格化された期待値 $\langle r|\boldsymbol{A}|r\rangle=1$ で表される図形の性質
さて少し前の例に戻って実エルミート行列(対称行列)
$$\boldsymbol{A}=\begin{pmatrix}
1 & \dfrac{1}{2}\\
\dfrac{1}{2} & 1
\end{pmatrix}$$
を規格化条件(11)式
$$\langle r|r\rangle=1 \tag{11}$$
に挿入した(20)式
$$\langle r|\boldsymbol{A}|r\rangle=1 \tag{20}$$
の性質を調べる。そのために対称行列を実ユニタリ行列(直交行列)によって対角行列
$$\boldsymbol{\Lambda}=\begin{pmatrix}
\dfrac{3}{2} & 0\\
0 & \dfrac{1}{2}
\end{pmatrix}$$
で表すと、(20)式は
$$\begin{align*}
\dfrac{3}{2}x^2+\dfrac{1}{2}y^2&=1\\
∴ \dfrac{x^2}{\left(\sqrt{\dfrac{2}{3}}\right)^2}+\dfrac{y^2}{(\sqrt{2})^2}&=1
\end{align*} \tag{21}$$
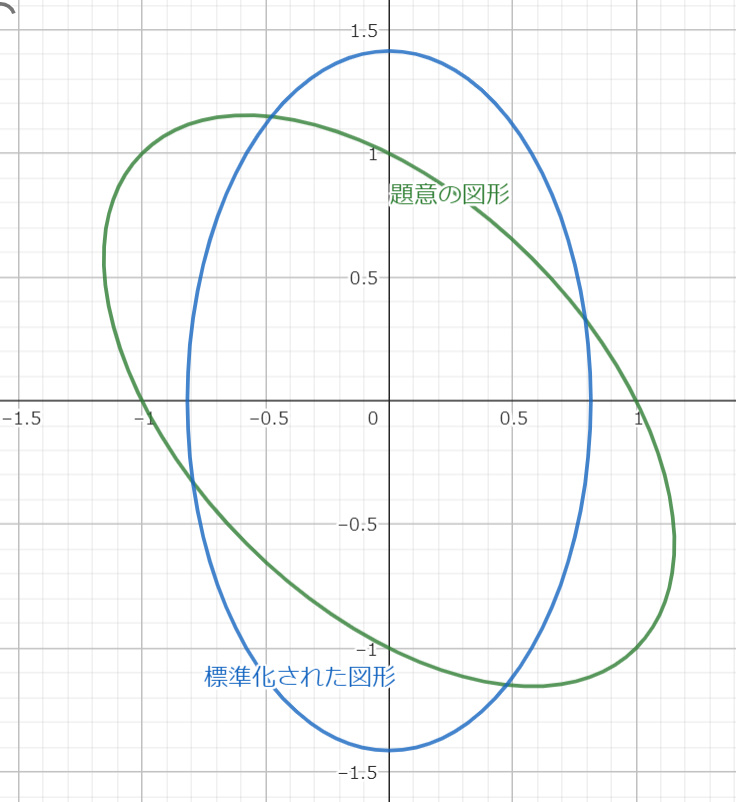
と変形される。このことから題意の図形は半長軸 $\sqrt{2}$ 、半短軸 $\sqrt{\dfrac{2}{3}}$ の楕円の性質を持つことが分かる。このように期待値 $\langle r|\boldsymbol{A}|r\rangle=1$ が対角行列の期待値 $\langle r|\boldsymbol{\Lambda}|r\rangle=1$ によって表現されるのなら、期待値 $\langle r|\boldsymbol{A}|r\rangle=1$ で表現される図形の性質が一目瞭然である。そこでこのように対角成分だけで表される二次形式 $λ_1x^2+λ_2y^2$ を標準的な状態とし、この形にすることを標準化と名付けよう。
規格化された期待値 $\langle r|\boldsymbol{A}|r\rangle=1$ はどう変換され標準化されるのか
さて行列 $\boldsymbol{A}$ とその対角行列 $\boldsymbol{\Lambda}$ の行列式は等しく
$$|\boldsymbol{A}|=|\boldsymbol{\Lambda}|=λ_1λ_2$$
となる。これは行列 $\boldsymbol{A}$ の対角化前後で行列のスケールが不変であることを意味する。
少し前にエルミート行列 $\boldsymbol{A}$ はユニタリ行列 $\boldsymbol{U}$ によって
$$\begin{align*}
\boldsymbol{U}^*\boldsymbol{A}\boldsymbol{U}&=\boldsymbol{\Lambda}\\
&=
\begin{pmatrix}
λ_1 & 0\\
0 & λ_2
\end{pmatrix}\end{align*}$$
のように対角化できると話した。そこでエルミート演算子 $\boldsymbol{A}$ の期待値へユニタリ行列 $\boldsymbol{U}$ を忍び込ませて
$$\langle r|\boldsymbol{A}|r\rangle=\langle \boldsymbol{U}^*r|\boldsymbol{\Lambda}|\boldsymbol{U}^*r\rangle$$
を得よう。なんだこの式と思われたら前回の記事
を確認するように。
この式は期待値を成すベクトル $|r\rangle$ をユニタリ行列 $\boldsymbol{U}$ の線型変換によるベクトルに置換したことになる。そこでエルミート演算子 $\boldsymbol{A}$ の期待値を
$$\begin{align*}
\langle r|\boldsymbol{A}|r\rangle&=\langle \boldsymbol{U}^*r|\boldsymbol{\Lambda}|\boldsymbol{U}^*r\rangle\\
&=\langle R|\boldsymbol{\Lambda}|R\rangle
\end{align*}$$
のようにユニタリ行列の逆行列 $\boldsymbol{U}^*$ による線型変換後のベクトル $\boldsymbol{U}^*|r\rangle=|R\rangle=(X,Y)$ によって置換することで、座標系 $(x,y)$ の行列 $\boldsymbol{A}$ の期待値からユニタリ行列の逆行列 $\boldsymbol{U}^*$ によって座標系 $(X,Y)$ における対角化された行列 $\boldsymbol{\Lambda}$ の期待値への変換と見なせる。
これはかなり画期的なことで、期待値を標準化するに当たってユニタリ行列 $\boldsymbol{U}$ によってどれだけ変換するのか分かるのである。
では先の例に挙げた対称行列 $\boldsymbol{A}$
$$\boldsymbol{A}=\begin{pmatrix}
1 & \dfrac{1}{2}\\
\dfrac{1}{2} & 1
\end{pmatrix}$$
を対角化する直交行列 $\boldsymbol{U}$ を求めるために、固有値 $λ=\dfrac{3}{2},\dfrac{1}{2}$ のそれぞれの固有ベクトル $\boldsymbol{r}$ を求める。
$λ_1=\dfrac{3}{2}$ のとき
$$\begin{align*}
(\boldsymbol{A}-λ_1\boldsymbol{I})\boldsymbol{r}=\begin{pmatrix}
-\dfrac{1}{2} & \dfrac{1}{2}\\
\dfrac{1}{2} & -\dfrac{1}{2}
\end{pmatrix}\boldsymbol{r}&=\boldsymbol{0}\\
∴ \begin{pmatrix}
1 & -1\\
0 & 0
\end{pmatrix}\boldsymbol{r}&=\boldsymbol{0}\\
∴ \boldsymbol{r}_1=\begin{pmatrix}
x\\
y
\end{pmatrix}
&=α\begin{pmatrix}
1\\
1
\end{pmatrix}
\end{align*}$$
となる。 $α$ は0以外の任意定数とする。また $λ_2=\dfrac{1}{2}$ についても同様に求めても良いが、対称行列の性質から異なる固有値に対する固有ベクトルが直交することからも、0以外の任意定数 $β$ を用いて
$$\boldsymbol{r}_2=β\begin{pmatrix}
-1\\
1
\end{pmatrix}$$
と表される。よって求める直交行列は $α,β=\dfrac{1}{\sqrt{2}}$ として、
$$\begin{align*}\boldsymbol{U}=\begin{pmatrix}\boldsymbol{r}_1 & \boldsymbol{r}_2\end{pmatrix}&=\begin{pmatrix}
\dfrac{1}{\sqrt{2}} & -\dfrac{1}{\sqrt{2}}\\
\dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}}
\end{pmatrix}\\
&=\begin{pmatrix}
\cos\dfrac{π}{4} & -\sin\dfrac{π}{4}\\
\sin\dfrac{π}{4} & \cos\dfrac{π}{4}
\end{pmatrix}\end{align*}$$
となる。これは座標系 $(x,y)$ から座標系 $(X,Y)$ への直交行列の逆行列 $\boldsymbol{U}^*$ による線型変換
$$\boldsymbol{U}^*|r\rangle=|R\rangle$$
により、元の図形は $-\dfrac{π}{4}$ だけ回転移動することで標準化された楕円(21)式
$$\dfrac{x^2}{\left(\sqrt{\dfrac{2}{3}}\right)^2}+\dfrac{y^2}{(\sqrt{2})^2}=1 \tag{21}$$
となる。まあ当然の結果になるのだが、直交行列による線型変換について、両辺の左から $\boldsymbol{U}$ を掛けると
$$|r\rangle=\boldsymbol{U}|R\rangle$$
となり、元の図形における座標系 $(x,y)$ は標準化された楕円の座標系 $(X,Y)$ から $\dfrac{π}{4}$ だけ回転移動させることで得られる。
以上の議論から
$$\begin{align*}
\langle r|\boldsymbol{A}|r\rangle&=1\\
∴ x^2+xy+y^2&=1
\end{align*}$$
で表現される図形は半長軸を $\sqrt{2}$ とし、半短軸を $\sqrt{\dfrac{2}{3}}$ とする楕円の性質を持ち、標準化された楕円
$$\dfrac{x^2}{\left(\sqrt{\dfrac{2}{3}}\right)^2}+\dfrac{y^2}{(\sqrt{2})^2}=1 \tag{21}$$
から $\dfrac{π}{4}$ だけ回転移動させたものである。
先にも言ったが、対角化前後で行列のスケールは不変である。このことから、当然ながら対角化前後の期待値
$$\begin{align*}
\langle r|\boldsymbol{A}|r\rangle&=1\\
\langle R|\boldsymbol{\Lambda}|R\rangle&=1
\end{align*}$$
で表される楕円の面積は不変である。よって題意の楕円は円 $x^2+y^2=1$ の各成分において $a=\dfrac{1}{\sqrt{λ_1}},b=\dfrac{1}{\sqrt{λ_2}}$ だけ拡大されたものであるから、題意の楕円の面積は
$$\begin{align*}
πab&=π\dfrac{1}{\sqrt{λ_1λ_2}} (λ_1,λ_2>0)\\
&=π|\boldsymbol{\Lambda}|^{-\frac{1}{2}}=π|\boldsymbol{A}|^{-\frac{1}{2}}\\
&=π(A_{11}A_{22}-A_{12}^2)^{-\frac{1}{2}}
\end{align*}$$
となる。
もっと一般的に $n$ 次元のデカルト座標系においても対称行列 $\boldsymbol{A}$ の期待値について $\langle r|\boldsymbol{A}|r\rangle=1$ で表現される題意の図形は、行列 $\boldsymbol{A}$ を直交行列 $\boldsymbol{U}$ を用いて別の座標系で対角化することができる。これにより題意の図形と等しい性質を持つ標準化された図形を得られる。このとき元の座標系から対角化後の座標系への変換 $\boldsymbol{R}=\boldsymbol{U}^*\boldsymbol{r}$ は回転行列の反回転方向の行列 $\boldsymbol{U}^*$ による同一スケールでの回転移動となる。
3次元であれば球や楕円体のような図形になる。4次元以降は読者の心の中で創造されたい。
ちょっと休憩
今回は規格化された期待値 $\langle r|\boldsymbol{A}|r\rangle=1$ で表される図形を詳しく説明してきた。実は今まで暗黙の条件として固有値について $λ_1,λ_2>0$ を認めていたのだ。次回はこれ以外の条件を認めてみることで楕円を自然に拡張していこうと思う。
初回
前回
次回



コメント