期待値をデカルト座標系で表現しよう

この記事は4部構成のシリーズ「期待値を図形的に解釈してみた」の第2部になります。このシリーズを通して楕円の方程式が示す意味や数学的背景を紹介していきます。第2部以降では第1部で考えた期待値を実際にデカルト座標系で図形的に解釈していこうと思います。そこで期待値をデカルト座標系で表現できるようにするためにはどのような演算子を内積に挿入するべきなのか考えていきます。他のサイトや参考書では全く触れられることのない内容となっていますが、そのまま無視するのは余りにも勿体無いと感じたため書きました。きっと楽しんでもらえると思います。

式番号は引き継ぎ

期待値から二次形式へ

期待値のデカルト座標系での振る舞い

ベクトル $|r\rangle$ が規格化されているときにはブラ－ケット記法を用いて

$$\langle r|r\rangle=1 \tag{11}$$

と表されるのであった。このときブラケットの中に演算子 $\boldsymbol{A}$ を挟んだときには

$$\langle r|\boldsymbol{A}|r\rangle=λ \tag{12}$$

のように期待値 $λ$ が得られる。そこで今考える系を取り敢えず馴染みのある2次元のデカルト座標系 $\boldsymbol{r}=(x,y)$ とし、ここで使用する演算子を行列 $A_{ij}$ とする。つまり

$$\boldsymbol{A}=\begin{pmatrix}
A_{11} & A_{12}\\
A_{21} & A_{22}
\end{pmatrix}$$

とすると規格化条件を示す(11)式は

$$\langle r|r\rangle=x^2+y^2=1 \tag{13}$$

となり、デカルト座標系では原点中心の単位円を与える。つまりデカルト座標系において(12)式の $λ$ とは、単位円の円周上にある位置ベクトル $\boldsymbol{r}$ の固有ベクトル $\boldsymbol{r}_i$ が得られる固有値である。

そこでデカルト座標系において(12)、(13)式がどのように振舞われるのか可視化してみようというのがここでの話である。デカルト座標系 $\boldsymbol{r}=(x,y)$ として(12)式を表現してみると

$$\begin{align*}\langle r|\boldsymbol{A}|r\rangle&=λ \tag{12}\\
A_{11}x^2+(A_{12}+A_{21})xy+A_{22}y^2&=λ \tag{14}
\end{align*}$$

となる。左辺のこの形は $x,y$ の2次式になっていることから二次形式と呼ばれる。これに対して線型変換を一次形式と呼ぶことがある。

では具体的に

$$\boldsymbol{A}=\begin{pmatrix}
1 & \dfrac{1}{2}\\
\dfrac{1}{2} & 1
\end{pmatrix}$$

として、取り敢えずこのときの固有値 $λ$ を求めてみる。つまり

$$\begin{align*}\boldsymbol{A}\boldsymbol{r}&=λ\boldsymbol{r}\\
∴ (\boldsymbol{A}-\boldsymbol{I}λ)\boldsymbol{r}&=\boldsymbol{0}\\
∴ \begin{pmatrix}\\
1-λ & \dfrac{1}{2}\\
\dfrac{1}{2} & 1-λ
\end{pmatrix}
\boldsymbol{r}&=\boldsymbol{0}
\end{align*}$$

を $\boldsymbol{r}≠\boldsymbol{0}$ の下 $λ$ について解く。このとき固有多項式

$$\begin{vmatrix}\\
1-λ & \dfrac{1}{2}\\
\dfrac{1}{2} & 1-λ
\end{vmatrix}
=(1-λ)^2-\frac{1}{4}=\left(λ-\dfrac{3}{2}\right)\left(λ-\dfrac{1}{2}\right)$$

が $0$ となれば良く、これを解くと $λ=\dfrac{3}{2},\dfrac{1}{2}$ となる。

ところで(13)式

$$\langle r|r\rangle=x^2+y^2=1 \tag{13}$$

の下で(14)式

$$\begin{align*}
\begin{pmatrix}x & y\end{pmatrix}\begin{pmatrix}
1 & \dfrac{1}{2}\\
\dfrac{1}{2} & 1
\end{pmatrix}
\begin{pmatrix}x\\y\end{pmatrix}&=λ\\
∴ x^2+xy+y^2&=λ
\end{align*}$$

が成り立つことから、

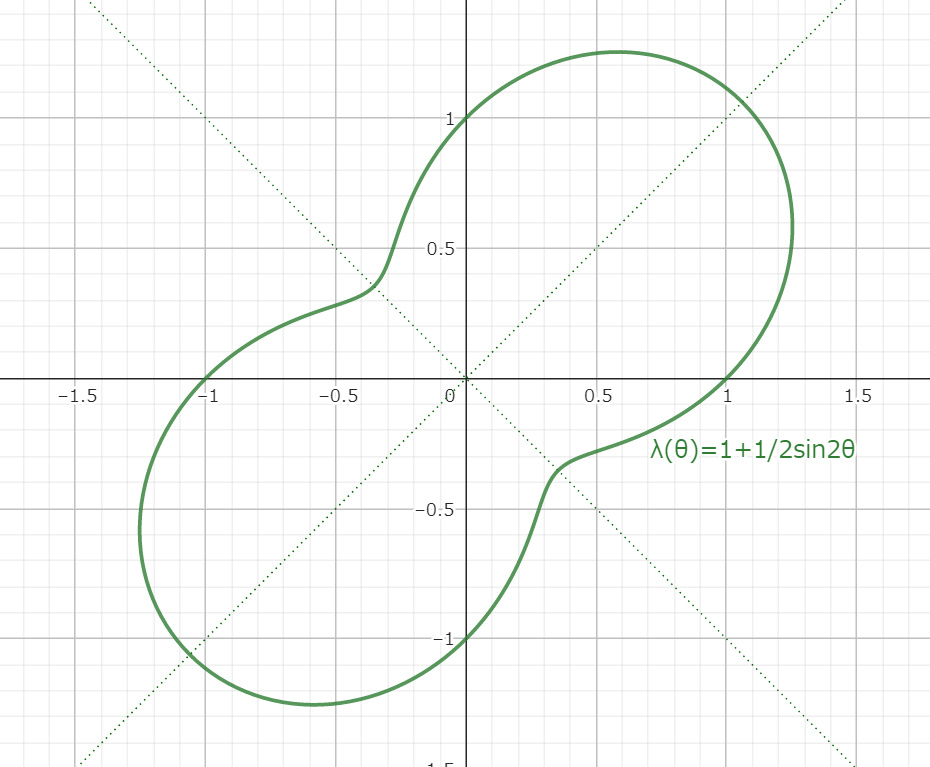
実際に
$$(θ,λ)=\left(\left\{\dfrac{π}{4},\dfrac{5π}{4}\right\},\dfrac{3}{2}\right),\left(\left\{\dfrac{3π}{4},\dfrac{7π}{4}\right\},\dfrac{1}{2}\right)$$

のように $θ$ の値によって $λ$ の値が定まる。

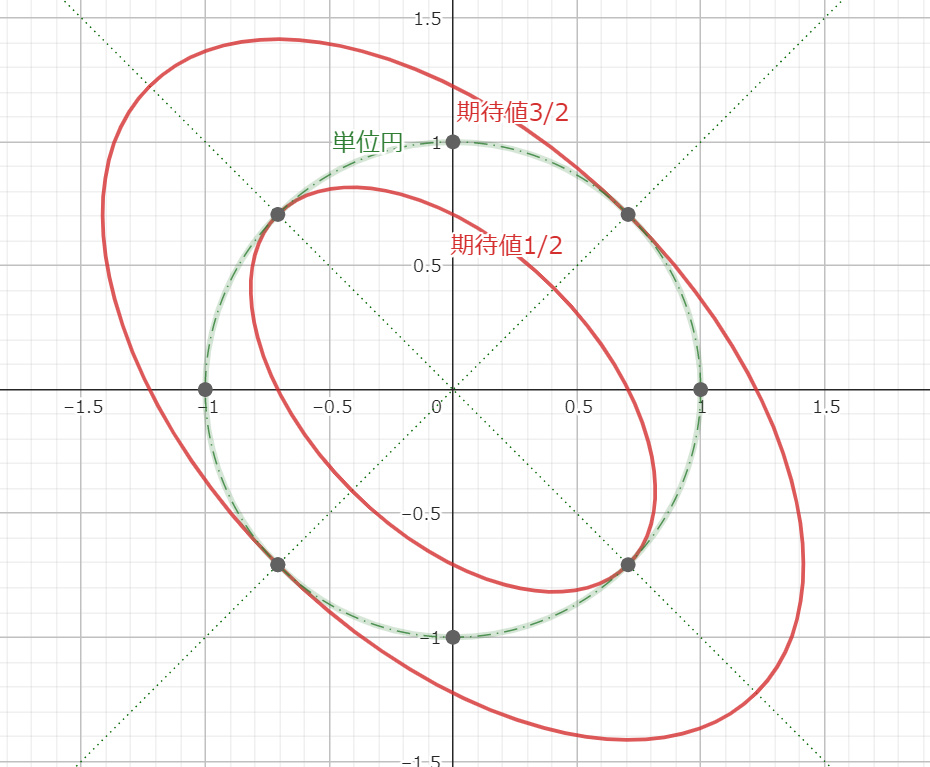
すると

$$θ=\left\{\dfrac{π}{4},\dfrac{5π}{4}\right\},\left\{\dfrac{3π}{4},\dfrac{7π}{4}\right\}$$

とは、それぞれの固有値について原点中心の単位円と(16)式との共有点のときの偏角 $θ$ となることが分かる。つまり得られる期待値とは、(16)式のそれぞれの期待値が固有値 $\dfrac{3}{2},\dfrac{1}{2}$ であるときの集合 $\boldsymbol{r}=(x,y)$ のうち、規格化条件(13)式

$$\langle r|r\rangle=x^2+y^2=1 \tag{13}$$

を満足するものである。

円を楕円に変形させる

さて規格化条件(13)式

$$\langle r|r\rangle=x^2+y^2=1 \tag{13}$$

の左辺に完全性を示す(3b)式

$$\int_{-∞}^∞\boldsymbol{\varphi}_{(x)}\boldsymbol{\varphi}_{(x)}^*dx=|φ_{(\boldsymbol{x})}\rangle\langle φ_{(\boldsymbol{x})}|=\boldsymbol{I} \tag{3b}$$

を

$$|r\rangle\langle r|=\boldsymbol{I} \tag{17}$$

としたものを挿入すると

$$\begin{align*}
\langle r|(|r\rangle\langle r|)|r\rangle&=1\\
∴ \langle r|\boldsymbol{I}|r\rangle&=1\\
∴ \begin{pmatrix}x & y\end{pmatrix}\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}
\begin{pmatrix}x\\y\end{pmatrix}&=1\\
∴ x^2+y^2&=1
\end{align*}$$

となる。そこで挿入する演算子を

$$\boldsymbol{A}=\begin{pmatrix}
\left(\dfrac{1}{a}\right)^2 & 0\\
0 & \left(\dfrac{1}{b}\right)^2
\end{pmatrix} \tag{18}$$

とすると、

$$\begin{align*}
\langle r|\boldsymbol{A}|r\rangle&=1\\
∴ \begin{pmatrix}x & y\end{pmatrix}\begin{pmatrix}
\left(\dfrac{1}{a}\right)^2 & 0\\
0 & \left(\dfrac{1}{b}\right)^2
\end{pmatrix}
\begin{pmatrix}x\\y\end{pmatrix}&=1\\
∴ \frac{x^2}{a^2}+\frac{y^2}{b^2}&=1
\end{align*} \tag{19}$$

となる。これを満たす $x,y$ は

$$\begin{cases}
x=a\cosθ\\
y=b\sinθ
\end{cases}$$

であるから、(19)式の演算子 $\boldsymbol{A}$ は単位円(13)式の $x,y$ をそれぞれ $a,b$ に拡大する作用素となる。つまり(19)式は楕円（条件によって双曲線にもなることがあるが、今は楕円だと思ってもらいたい）である。 $a,b$ のうち長い方が半長軸となり、短い方が半短軸となる。

このことから規格化条件(13)式

$$\langle r|r\rangle=x^2+y^2=1 \tag{13}$$

に挿入する演算子を(18)式のように対角行列で書けるのなら、

$$\begin{align*}\\
A_{11}x^2+(A_{12}+A_{21})xy+A_{22}y^2&=1\\
∴ \langle r|\boldsymbol{A}|r\rangle&=1
\end{align*}$$

で表される図形について、その特徴を知ることができよう。そこでどんな演算子を挿入してやるべきか考えてみよう。

内積への挿入に適した演算子はどれか

まず1つ対角化可能であることが挙げられる。対角化可能ではないということは各成分 $r_i$ についてどれだけ拡大縮小されているのか分からない。つまり各成分に対応するだけの固有値 $λ_i$ 、固有ベクトル $\boldsymbol{r}_i$ が得られるべきである。

次に対角化したときに任意の対角成分が実数であると嬉しい。折角デカルト座標系で考えているのだから、最終的に実数で表現されなければ何が何だかよく分からなくなってしまう。

そしてユニタリ行列によって行列が対角化可能なら大変喜ばしい。これはとある行列 $\boldsymbol{A}$ をユニタリ行列 $\boldsymbol{U}$ によって

$$\begin{align*}
\boldsymbol{U}^*\boldsymbol{A}\boldsymbol{U}&=\boldsymbol{\Lambda}\\
&=
\begin{pmatrix}
λ_1 & 0\\
0 & λ_2
\end{pmatrix}\end{align*}$$

のように対角行列で表されるのなら、

$$\begin{align*}
\langle r|\boldsymbol{A}|r\rangle&=\langle r|(\boldsymbol{U}\boldsymbol{U}^*)\boldsymbol{A}(\boldsymbol{U}\boldsymbol{U}^*)|r\rangle　(∵ \boldsymbol{U}\boldsymbol{U}^*=\boldsymbol{I})\\
&= \langle r|\boldsymbol{U}(\boldsymbol{U}^*\boldsymbol{A}\boldsymbol{U})\boldsymbol{U}^*|r\rangle\\
&=\langle r|\boldsymbol{U}\boldsymbol{\Lambda}\boldsymbol{U}^*|r\rangle\\
&=\langle \boldsymbol{U}^*r|\boldsymbol{\Lambda}|\boldsymbol{U}^*r\rangle\\
\end{align*}$$

のように期待値 $\langle r|\boldsymbol{A}|r\rangle$ の中にバレずに忍び込んで、 $\boldsymbol{A}$ を対角行列にしてしまえるので超便利である。そのため単に期待値を

$$\langle r|\boldsymbol{\Lambda}|r\rangle=λ_1x^2+λ_2y^2=1$$

と置くだけで題意の図形がどんな性質を持つのか一目で分かるのである。

これらの考察から期待値1で表される図形

$$\langle r|\boldsymbol{A}|r\rangle=1 \tag{20}$$

をエルミート演算子 $\boldsymbol{A}$ によって表現すれば、

• ユニタリ行列 $\boldsymbol{U}$ によって対角化可能
• 固有値は全て実数

である。なおデカルト座標系では、期待値

$$\langle r|\boldsymbol{A}|r\rangle=1 \tag{20}$$

を考えるときに挿入する演算子がエルミート行列であったとしても、

$$A_{12}=\overline{A}_{21}$$

であるため、

$$\begin{align*}
&A_{11}x^2+(A_{12}+A_{21})xy+A_{22}y^2\\
&=A_{11}x^2+2\Re(A_{12})xy+A_{22}y^2
\end{align*}$$

となる。つまり $A_{12}$ と $A_{21}$ は複素共役であるなら、これらの虚部はデカルト座標系においてはなんでも良い。結局実空間でかんがえるのなら対称行列の計算となる。

他のサイトではこのことを詳しく説明せずにただ $\boldsymbol{A}$ を対称行列として、さも当然の如く対角化しているのだが、実はこんな背景があったとさ。

ちょっと休憩

この記事では二次形式という立場から、デカルト座標系において期待値がどのように描かれるのか考えてきた。今回は暗に条件を制約して楕円の形となるようにしたが、次回ではこの条件を変えることで楕円の方程式を他の図形に拡張してみようと思う。