本記事は4部構成のシリーズ「期待値を図形的に解釈してみた」の第4部になります。このシリーズを通して楕円の方程式が示す意味や数学的背景を紹介していきます。第4部では今まで考えてきた規格化された期待値 $\langle r|\boldsymbol{A}|r\rangle=1$ で表される図形について、暗黙の条件として認めていた固有値についての条件 $λ_1,λ_2>0$ を自然に拡張してみようと思います。つまり本来は楕円ではない図形でも楕円の方程式の下で示されるのです。
初回
前回
次回
予定なしよ。
期待値から二次形式へ
二次形式の図形を楕円の方程式から拡張する
何度もちょくちょく触れているが2次元の二次形式で表される図形は、条件により楕円、双曲線、……等形が変わるのである。これまでに行列式のスケールが固有値の積 $λ_1λ_2$ で表されることを利用して楕円の面積を求めてきた。しかし実際には固有値 $λ$ は実数を取り得ることから、このスケール $λ_1λ_2$ も正の値のみを取るわけではない。つまり行列式のスケールについて、楕円の面積が正の値以外を取るという解釈の下で、何かこれを満たすような図形をデカルト座標系で描くことができるはずだ。以降簡単のため対角化行列 $\boldsymbol{\Lambda}$ の期待値を求める。
虚の楕円
まず対角化行列 $\boldsymbol{\Lambda}$ を挿入した規格化された期待値
$$\langle r|\boldsymbol{\Lambda}|r\rangle =1 \tag{20}$$
について、この右辺が実定数 $c$ 倍されるということは、図形全体のスケールが $c$ 倍されるということである。つまり挿入する行列 $\boldsymbol{A}$ の固有値も全て $c$ 倍される。よって(20)式で表される $n$ 次元の楕円のスケールは $\sqrt{c}^n$ 倍される。
そこで $c=-1$ 倍された2次元の期待値(20)式を規格化すると
$$\begin{align*}
\langle r|\boldsymbol{\Lambda}|r\rangle =-1\\
∴ λ_1x^2+λ_2y^2=-1\\
∴ -λ_1x^2-λ_2y^2=1
\end{align*} \tag{22}$$
となる。よって $a=\dfrac{1}{\sqrt{λ_1}i},b=\dfrac{1}{\sqrt{λ_2}i}$ となるが、このとき期待値の左辺は常に負の値を取るため、これを規格化する実数 $x,y$ は存在しない。これは規格化された期待値 $\langle r|\boldsymbol{\Lambda}|r\rangle =1$ が固有値 $λ_1,λ_2$ について $λ_1<0かつλ_2<0$ となり得ないことを意味する。この図形はデカルト座標系には一切現れないことと、(22)式は(20)式と比較して $a,b$ を大きさの等しい純虚数に取っていることから、(22)式は(20)式についての虚の楕円と呼ばれることもある。
双曲線
次に $λ_1,λ_2$ が異符号のときを考えてみる。ここでは $λ_1=-λ_1^+<0,λ_2=λ_2^+>0$ として $a=\dfrac{1}{\sqrt{λ_1^+}i},b=\dfrac{1}{\sqrt{λ_2^+}}$ の場合のみを考える。期待値は $x,y$ の対称式となっていることから $λ_1>0,λ_2=-λ_2^+<0$ の場合には $\dfrac{π}{2}$ だけ回転移動させたことになるから $λ_1=-λ_1^+<0,λ_2>0$ と定めても対称性は失われない。
さて虚数単位を $i=-\sqrt{-1}$ と置くと、 $a=\dfrac{1}{\sqrt{λ_1^+}(-i)},b=\dfrac{1}{\sqrt{λ_2^+}}$ のときには楕円の面積は
$$\begin{align*}
πab&=πi\dfrac{1}{\sqrt{λ_1^+λ_2^+}} (λ_1^+,λ_2^+>0)\\
&=π|\boldsymbol{\Lambda}|^{-\frac{1}{2}}
\end{align*}$$
となり、虚数ではあるもののある値に定まることが分かる。
虚数単位の定義の仕方に対して「ズルじゃん!」と思った読者は
の見出し『虚数単位 $i$ とは何か』を読んでもらいたい。
さて $λ_1<0かつλ_2<0$ のときには虚の楕円の面積は $πab≠π|\boldsymbol{\Lambda}|^{-\frac{1}{2}}$ となり、行列式では定義できない。それなら固有値 $λ_1,λ_2$ が異符号のときにはデカルト座標系において何らかの図形となりそうである。
よって固有値 $λ_1,λ_2$ が異符号のときの標準化された楕円は
$$\begin{align*}
\langle r|\boldsymbol{\Lambda}|r\rangle &=1\\
∴ -λ_1^+x^2+λ_2^+y^2&=1 (λ_1^+,λ_2^+>0)\\
∴ \frac{x^2}{a^2}+\frac{y^2}{b^2}&=1
\end{align*}$$
となる。これは双曲線を表す。
平行な2直線
次に $λ_1=-λ_1^+<0,λ_2=0$ となる場合にデカルト座標系でどのように描かれるのか考えたい。ここで $λ_2<0$ となると虚の楕円となってしまうことから、$λ_2=0$ を $\displaystyle\lim_{ε→+0}ε$ を満たす極限値 $λ_2$ とする。すると例により虚数単位を $i=-\sqrt{-1}$ と置くと
$$a=\dfrac{1}{\sqrt{λ_1^+}(-i)}, b=\lim_{ε→+0}\dfrac{1}{\sqrt{ε}}$$
のときには楕円の面積は
$$\begin{align*}
πab&=\lim_{ε→+0}πi\dfrac{1}{\sqrt{ελ_1^+}} (λ_1^+>0)\\
&=\lim_{ε→+0}π|\boldsymbol{\Lambda}|^{-\frac{1}{2}}\\
&→同じように発散する
\end{align*}$$
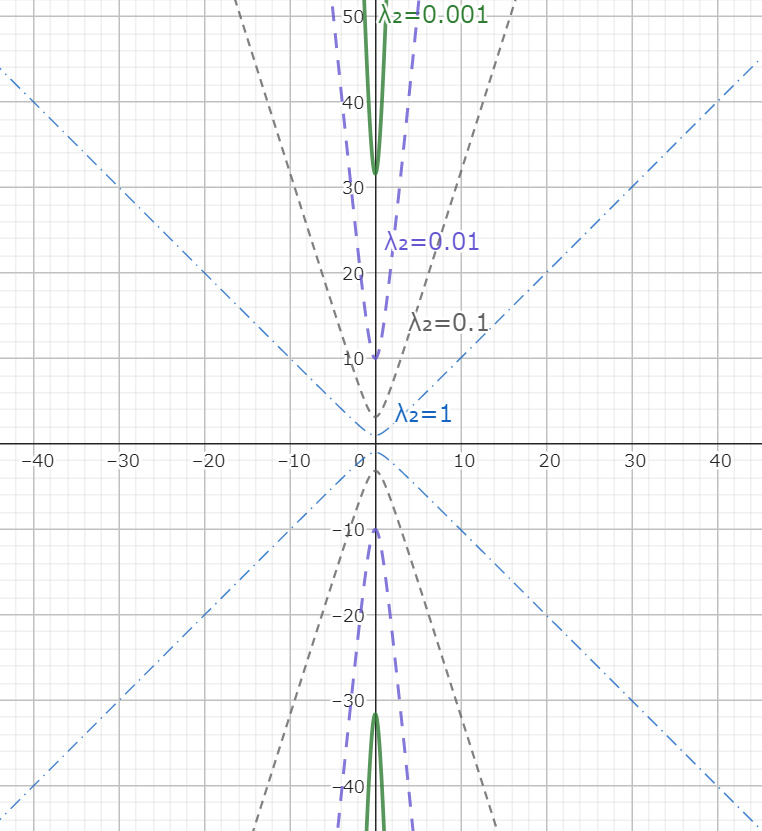
かなりざっくり過ぎて数学の専門家様に怒られそうだが、図を見ればそういうことである。
次に $λ_1=λ_1^+>0,λ_2=0$ となる場合について。このとき $λ_2$ は正負どちらも取り得ることから $λ_2=0$ は $\displaystyle\lim_{ε→0}ε=\lim_{ε±→0}ε$ となる。
例により虚数単位を $i=-\sqrt{-1}$ と置くと
$\displaystyle\lim_{ε→+0}$ のとき即ち
$$a=\dfrac{1}{\sqrt{λ_1^+}(-i)}, b=\lim_{ε→+0}\dfrac{1}{\sqrt{ε}}$$
のときには楕円の面積は
$$\begin{align*}
πab&=\lim_{ε→+0}π\dfrac{1}{\sqrt{ελ_1^+}} (λ_1^+>0)\\
&=\lim_{ε→+0}π|\boldsymbol{\Lambda}|^{-\frac{1}{2}}\\
&→同じように正に発散する
\end{align*}$$
$\displaystyle\lim_{ε→-0}$ のとき即ち
$$a=\dfrac{1}{\sqrt{λ_1^+}(-i)}, b=\lim_{-i\sqrt{ε}→+0}\dfrac{1}{-i\sqrt{ε}}$$
のときには楕円の面積は
$$\begin{align*}
πab&=\lim_{-i\sqrt{ε}→+0}π\dfrac{1}{-i\sqrt{ε}\sqrt{λ_1^+}} (λ_1^+>0)\\
&=\lim_{-i\sqrt{ε}→+0}π|\boldsymbol{\Lambda}|^{-\frac{1}{2}}\\
&→同じように正に発散する
\end{align*}$$
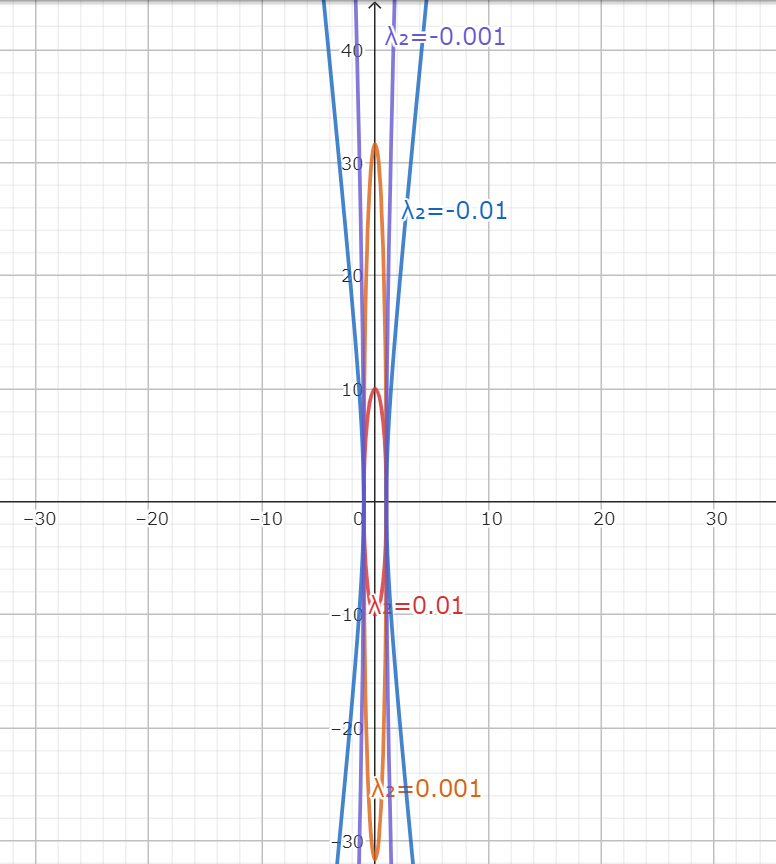
よって $λ_1=λ_1^+>0,λ_2=0$ となるときには標準化された楕円は平行な2直線となる。
直線
では2直線を限りなく近づけたらどうなるのか気になるところであろう。そこで$λ_1=-λ_1^+→∞,λ_2=0$ となるときを調べる。このとき $\displaystyle λ_1=\lim_{ε→∞}ε, λ_2=\lim_{δ→0}δ$ と置くと、
$$a=\lim_{ε→∞}\dfrac{1}{\sqrt{ε}}, b=\lim_{δ→0}\dfrac{1}{\sqrt{δ}}$$
となる。よって
$$\begin{align*}
πab&=\lim_{ε→∞}\dfrac{1}{\sqrt{ε}}\lim_{δ→0}\dfrac{1}{\sqrt{δ}}\\
&=\lim_{ε→∞}\lim_{δ→0}π|\boldsymbol{\Lambda}|^{-\frac{1}{2}}\\
&→同じように不定形
\end{align*}$$
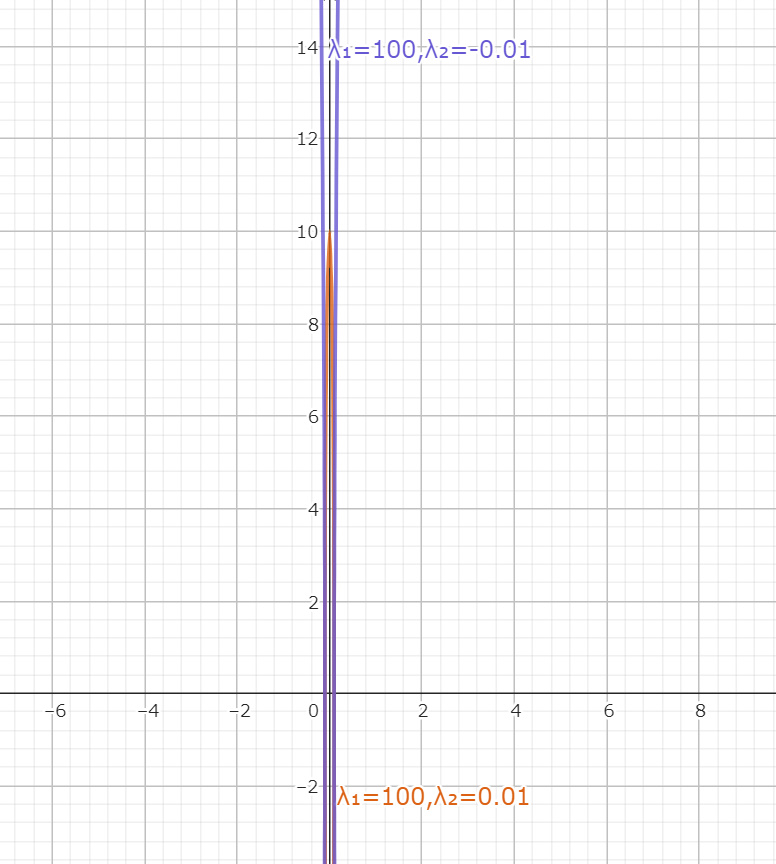
となる。このとき標準化された楕円は直線となる……のだが、楕円の面積が不定形になってしまう。そこで行列式 $|\boldsymbol{\Lambda}|$ が正の定数 $\frac{1}{A^2}$ に定まっているという制約条件の下考えてみよう。つまり
$$|\boldsymbol{\Lambda}|=λ_1λ_2=\frac{1}{A^2}$$
を満たすように極限
$$\lim_{a→0}\lim_{b→∞}ab=A \tag{23}$$
を取る。すると(23)式の条件の下で(20)式
$$\begin{align*}\langle r|\boldsymbol{\Lambda}|r\rangle &=1\\
∴ λ_1x_1^2+λ_2x_2^2&=1
\end{align*} \tag{20}$$
の行列式を考えることになる。
さてある成分 $x_{k'(=1,2)}$ の係数 $a_{k’}$ が正の発散をし、それ以外の係数 $a_{k}$ が0に収束するとすると、$f_{(x_k)}$ が定数関数 $f_{(x_k)}=A$ となる下で
$$\begin{align*}
ab&=\int_{-∞}^{∞}δ_{(x_k-x_{k’})}f_{(x_k)}d^2x_k\\
&=f_{(x_k’)}\int_{-∞}^{∞}δ_{(x_k-x_{k’})}d^2x_k\\
&=f_{(x_k’)}=A
\end{align*}$$
となる。ただし $δ_{x_k,x_{k’}}$ はデルタ関数である。なおこれを $n$ 次元の下で拡張すると
$$\prod_{k=1}^na_k=\int_{-∞}^∞δ_{(x_k-x_{k’})}f_{(x_k)}d^nx_k=f_{(x_{k’})}$$
となる。固有値が連続的に取り出せる場合には
$$\prod_{k=1}^∞a_k=\int_{-∞}^∞δ_{(x_k-x_{k’})}f_{(x_k)}d^∞x_k=f_{(x_{k’})}$$
と表される。よって楕円の面積は
$$\begin{align*}
πa_1a_2&=π|\boldsymbol{\Lambda}|^{-\frac{1}{2}}\\
&=πA
\end{align*}$$
となる。
最後に
今回は楕円の方程式を拡張することで標準化された双曲線や直線の方程式を得ることができた。デカルト座標系において規格化条件は単位円となるが、これを平行移動させた
$$\langle r-P|r-P\rangle=(x-u)^2+(y-v)^2$$
で期待値を考えれば、期待値で表される図形は $\boldsymbol{P}=(u,v)$ だけ平行移動されたものになる。またこれらは二次曲線という枠組みで括られることがあるが、これは二次形式で表されないような二次式(例えば $xy+y^2=1$ 等)も含有する。なお3次元における二次形式は三次曲面と言われる。
また規格化条件を
$$\langle r|r^2\rangle=x^3+y^3=1$$
のように二次形式のケット $|r^2\rangle$ で考えれば三次形式なるものが得られるが、ちょっとこの議論は難しすぎるので今はまだ余白が狭すぎるのである。
初回
前回
次回
予定なしよ。



コメント