前書き
本記事はシリーズ『非調和比をそれっぽく解釈する』の第4部になります。
前回
次回
予定なし
本記事では比の値を更に比にしたもの、つまり比の値を複合したものを非調和比（複比）と呼びます。非調和比は射影幾何学における調和性を考えるときに用いられますが、複素数平面などの射影幾何学以外の分野では複比という言葉が広く使われています。ここでは、複素数平面上においても調和性を感じていただくために非調和比という言葉を採用します。
また2つの定点を基準とした一次分数関数同士の比の値を取ることで、2つの定点の分割点による分割比率の比の値は、非調和比となります。
この非調和比の概念は実数の範囲に指定すれば数直線上の非調和比となり、複素数平面上で表現したければ複素数の範囲で指定すれば良いというように、非常に広範な適用性を持っています。
非調和比（複比）
比の値とはある比 a:b があったときに ab のように比率で表現するものだった。この比の値を更に比にしたもの、つまり
ab:cd
のように比の値を複合したものを非調和比（複比）と言う。非調和比という名前は射影幾何学における調和性を考えるときに用いられることがある。しかし複素数平面などの射影幾何学以外の分野では複比という言葉が広く使われているように感じる。ここでは複素数平面上においても調和性を感じてほしいので非調和比という言葉を採用していく。
一次分数関数
w(z)=z−z1z−z2
は2つの定点 A(z1),B(z2) を点 C(z) による分割したときの値を表わしていたのだった。ここで分割点 C(z) の基準点 A(z1),B(z2) を強調して (z1,z2;z)=w(z) と置くことにしよう。こうすれば z はどのように分割する点なのか分かりやすい。
次に同様に分割点 D(z′) による一次分数関数を (z1,z2;z′)=w(z′) と置く。
更にこれらの一次分数関数を考えると
(z1,z2;z)(z1,z2;z′)
となるが、分母と分子は同一の基準点 A(z1),B(z2) となっているので
(z1,z2;z,z′)
と置こう。具体的には以下のような比
(z1,z2;z):(z1,z2;z′)=z−z1z−z2:z′−z1z′−z2
に関する比の値となる。このように2つある3点の分割比率の比の値とは非調和比（複比）となる。
ここでは各点の取りうる値の範囲は指定していないが、実数の範囲に指定すれば数直線上の非調和比となり、複素数平面上で表現したければ複素数の範囲で指定すれば良い。また射影幾何学では非調和比は射影直線上の集合に関連付けられる。いずれにせよより一般的には任意の体の元にも適用できるのである。
また非調和比は点 A(z1),B(z2),C(z),D(z′) のうちいずれかの点が無限大の場合には、無限大となる点を含む箇所を削除することで得られる。例えば基準点の1つ B(z2) を無限大とすると、
(z1,∞;z3,z4)=z4−z1z3−z1
となり、これは形式的に
(z1;z3,z4)
と表わされ、分数の性質から (z3,z4;z1) と値が等しくなる。
一次分数変換の非調和比は不変
実は一次分数変換の非調和比は不変であるようなので確認してみよう。
また例によって c≠0,ad−bc≠0 とする。第2式は0で割らないようにするための布石だ。
任意の4点 z1,z2,z3,z4 がそれぞれ一次分数変換
az+bcz+d (a,b,c,d∈Z)
によって w1,w2,w3,w4 に変換されるとする。このとき
w3−w1=az3+bcz3+d−az1+bcz1+d=(az3+b)(cz1+d)−(az1+b)(cz3+d)(cz3+d)(cz1+d)=(ad−bc)(z3−z1)(cz3+d)(cz1+d)w3−w2=(ad−bc)(z3−z2)(cz3+d)(cz2+d)
となる。よって
w3−w1w3−w2=(ad−bc)(z3−z1)(cz3+d)(cz1+d)⋅(cz3+d)(cz2+d)(ad−bc)(z3−z2)=cz2+dcz1+d⋅z3−z1z3−z2
同様に
w4−w1w4−w2=cz2+dcz1+d⋅z4−z1z4−z2
となるから、これらの比を取ると
w4−w1w4−w2:w3−w1w3−w2=z4−z1z4−z2:z3−z1z3−z2
となる。これにより非調和比が一次分数変換で不変であることが示された。
なお比の内項・外項の積が等しいことから、
w4−w1w4−w2⋅z3−z1z3−z2=w3−w1w3−w2⋅z4−z1z4−z2∴w4−w1w4−w2=(z3−z2z3−z1⋅w3−w1w3−w2)z4−z1z4−z2∴w4−w1w4−w2=Kz4−z1z4−z2
のように表される。ただし
K=z3−z2z3−z1⋅w3−w1w3−w2
と置いた。これにより不動点の個数によらず(25)式が成り立つことが分かる。
また(25)式の比の値
w4−w1w4−w2w3−w1w3−w2=z4−z1z4−z2z3−z2z3−z1=k
が実数 k となるのであれば、
4点 z1,z2,z3,z4 が同一円周上または同一直線上
であることと
4点 w1,w2,w3,w4 が同一円周上または同一直線上
であることが言える。
つまり3点 z1,z2,z3 が定点なら、これらが成す「円周または直線」に点 z4 は存在し、3点 w1,w2,w3 が定点なら、これらが成す「円周または直線」に点 w4 は存在する。
よって(26)式は z4,w4 を変数 z,w に置き換えて
w−w1w−w2=Kz−z1z−z2
と書けば、2つの変数 z,w は4つの定点 z1,z2,w1,w2 と定数 K (定点 z3,w3 に依存)によって定まることが分かる。
なお(26)式は式変形して
w=az+bcz+d
のように一次分数変換の形で表されるので、3点 z1,z2,z3 とその変換後の3点 w1,w2,w3 が分かれば、(25)式 のように変形可能であることが確認できる。
よって前の例で示した(15)式
w−αw−β=kz−αz−β
とは定点を z1=w1=α,z2=w2=β となるように不動点 α,β とした(26)式のことである。
非調和群
非調和比は2つの分数を分数で表現しているのだった。そのため例えば点 A,B,C,D を用いた非調和比は順序を入れ替えることで幾つか等しい値となる。
例えば
(A,B;C,D)=(B,A;D,C)=(C,D;A,B)=(D,C;B,A)
となる。これらは各辺は最左辺の順列の並び替えとなるので、最左辺を1として各辺の順列は
1,(ABCDBADC),(ABCDCDAB),(ABCDDCBA)
となる。或いは循環表記法を用いて
1,(A,B)(C,D),(A,C)(B,D),(A,D)(B,C)
と表現すれば、4通りの互換の積置換（偶置換）で表されていることが分かる。またそれぞれの置換は及ぼし合わないので、各辺の合成置換は入れ替えても値は変わらない。つまり4つの対象群の作用と考えられる。
勿論非調和比はこれだけではなく、これを含めて B,C,D を並び替えた非調和比が 3!=6 通りあるはずだ。実際に非調和比は以下の6通り存在する。
(A,B;C,D)=λ (A,B;C,D)=1λ(A,C;D,B)=11−λ (A,C;B,D)=1−λ(A,D;C,B)=λλ−1 (A,D;B,C)=λ−1λ
それぞれの非調和比による変換は z を分数とした一次分数変換となり、これらの6つの変換は6要素の群に対する部分群を形成する。
そこでそれぞれの部分群について不動点 λ不動 を求めると
λ不動={−1,(1),(1λ)12,(1−λ)2,(0),(∞)
となる。不動点とはグラフで言えば y=λとy=f(λ) の共有点となる点のことである。なお()で表現した値は点 A,B,C,D が全て異なる場合には取りえず、互いに接近するときの極限値である。
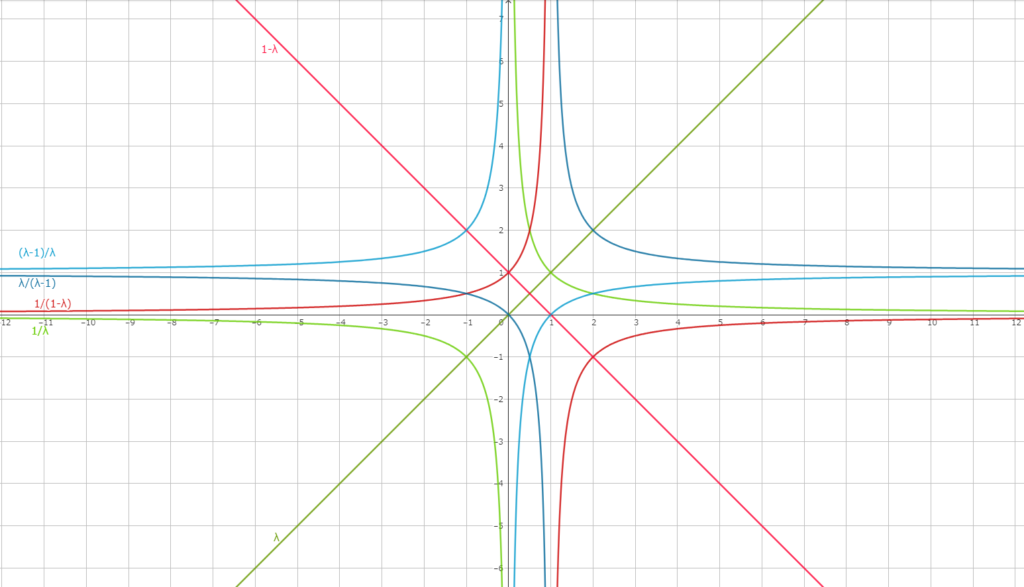
y=λと共有点を持たないものもあるが……
しかし残りの2つ 11−λ,λ−1λ は直線 y=λ とグラフ上では共有点を持たない。そこで実際に方程式を立てて複素数に拡張して不動点を求めると、
λ不動=1±√3i2=e±iπ/3 (11−λ,λ−1λ)
ただし複合同順とする。
よって非調和比の部分群は
{1λ,1−λ,λλ−1}と{11−λ,λ−1λ}
とで分けることができる。また λ が固有点となる場合には対称性が高くなるので、取りうる値は6よりも少なくなる。
左の部分群は2つの不動点の集合 {−1,12,2},{0,1,∞} を持ち、右の部分群は1つの不動点の集合 {eiπ/3,e−iπ/3} となる。これらの不動点は各集合で閉じているので読者に確認を任せる。
最後に
非調和比の性質を説明するために、複素数平面や比の値の知識を改めて紹介しながら進めてきた。射影幾何学では、非調和比はその名称から線分の調和性を感じることができるので、興味のある読者はそちらの方面にも足を運んでもらいたい。
コメント