前書き
本記事はシリーズ『非調和比をそれっぽく解釈する』の第3部になります。
初回
前回
次回
本記事では一次分数変換について考察します。一次分数変換とは複素数平面上の点を用いて、2つのベクトルの比の値を求める方法です。具体的に複素数平面上の2つの定点 $A(z_1),B(z_2)$ を点 $(z)$ によって分割したときの比の値を求めます。
この比の値は一次分数関数 $w(z)$ として表現されます。また、一次分数関数 $w(z)$ で表される複素数の変換を一次分数変換と言い、これを何度も繰り返すと複素数平面上でどのように振る舞うのかを調べます。
なお一次分数変換の詳しい図形的な意味については別の機会にでも紹介しましょう。
一次分数変換とは
ここで複素数平面上の点 $A(z_1),B(z_2),C(z_3),D(z_4)$ を置く。するとそれぞれが2次元平面のデカルト座標系の各点に対応するのだから、
$$
\dfrac{z_2-z_1}{z_4-z_3} \tag{10}
$$
とは、2つのベクトル $AB,CD(∈\mathbb{R}^2)$ の比の値となる。
或いは簡単のために始点を共通にして
$$\begin{align*}
&\dfrac{z_1-z}{z_2-z} \\
もしくは &\dfrac{z-z_1}{z-z_2} \tag{11}
\end{align*}$$
のように置くと、これは角度 $∠z_2zz_1$ を挟む2つのベクトルの比の値となる。
つまり(11)式の比の値を $w(z)$ と置くと、 $w(z)$ は複素数平面上の2つの定点 $A(z_1),B(z_2)$ を点 $(z)$ によって分割したときの比の値($∈\mathbb{C}$)となる。
例えば $z_1=1+2i, z_2=4-i$ とするときに、これらを $1:2$ に内分する点を求めてみる。
まず $1:2$ に内分するについてだが、複素数平面上では角度 $∠z_2zz_1=π$ を挟むと言える。つまり $1:2$ に内分するときの比の値は
$$
\dfrac{1}{2} (\cos π+i\sin π) = -\dfrac{1}{2}
$$
となるから(11)式により比の値に関する方程式
$$
\dfrac{(1+2i)-z}{(4-i)-z} = -\dfrac{1}{2}
$$
を解くと
$$\begin{align*}
∴2((1+2i)-z) &= -((4-i)-z) \\
∴3z &= 6+3i \\
∴z &= 2+i
\end{align*}$$
を得る。これは複素数の内分点の公式から導いても同じ値となる。
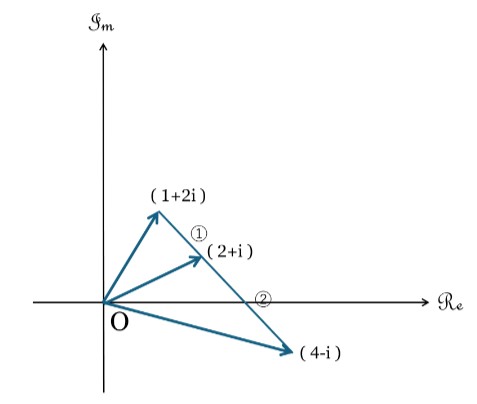
また外分点の場合には角度 $∠z_2zz_1=0$ を挟むとして同様の計算をすれば求まる。
いずれにせよ比の値が実数となるように分割する場合には、3点 $A(z_1),B(z_2),(z)$ は複素数平面上において同一直線上にあるのだ。
また始点が違う一般の場合には $(az),(bz)$ のように共通の複素数 $z$ を用いて、
$$
\dfrac{az-z_1}{bz-z_2} \tag{12}
$$
のように置けば複素数zによる一次分数関数 $w(z)$ で表わすことができる。この $z→w$ の変換を $z$ による一次分数変換と言う。
では一次分数関数 $w(z)$ を何度も繰り返すと、複素数平面上でどのように振る舞うのだろうか。
一次分数変換を何度も繰り返すと……?
不動点が2個の場合
例. ある $z_0$ が与えられている数列 $z_n(n\geq 0)$ が漸化式
$$
z_{n+1} = \dfrac{2z_n +1}{z_n +2} \tag{13}
$$を満たすとき、この数列 $\{z_n \}$ の複素数平面上での振る舞いを調べる。
まず一次分数変換
$$
w= \dfrac{2z +1}{z +2} \tag{14}
$$
の不動点を $α,β(α>β)$ とすると
$$
\dfrac{w-α}{w-β} = k \dfrac{z-α}{z-β} \tag{15}
$$
の形に変形されることを示そう。
不動点とは何度変換しても変わらない不動の点という意味であるのは言うまでもない。つまり $z$ に関する方程式
$$
z= \dfrac{2z +1}{z +2} \tag{16}
$$
の解が不動点となる。よってこれを解いて
$$\begin{align*}
z(z+2) &= 2z+1 \\
∴ z^2&=1 \\
∴ z&=±1
\end{align*}$$
故に不動点は $α=1,β=-1$ となる。
よって(15)式は
$$\begin{align} \dfrac{w-1}{w+1} &= \dfrac{z-1}{3z+3} \\
&= \dfrac{1}{3} \dfrac{z-1}{z+1} \end{align}$$
となる。なお2つの不動点がある場合には(15)式のように変形できるので、意欲のある読者は調べてみていただきたい。
これを与えられた漸化式に用いると
$$
\dfrac{z_{n+1} -1}{z_{n+1} +1} = \dfrac{1}{3} \dfrac{z_n -1}{z_n +1} \tag{17}
$$
となり、これにより数列 $\dfrac{z_n -1}{z_n +1}$ は公比 $\dfrac{1}{3}$ 、初項 $\dfrac{z_0}{z_0}$ の等比数列
$$
\dfrac{z_n -1}{z_n +1} = \left(\dfrac{1}{3} \right)^n \dfrac{z_0 -1}{z_0 +1} \tag{18}
$$
となる。更に両辺の偏角を調べると
$$\begin{align*} arg \left(\dfrac{z_n -1}{z_n +1} \right) &= arg \left( \left(\dfrac{1}{3} \right)^n \dfrac{z_0 -1}{z_0 +1} \right) \\ &=arg \left(\dfrac{1}{3} \right) ^n+arg \left(\dfrac{z_0 -1}{z_0 +1} \right) \\ &=arg \left(\dfrac{z_0 -1}{z_0 +1} \right) \end{align*} \tag{19}$$
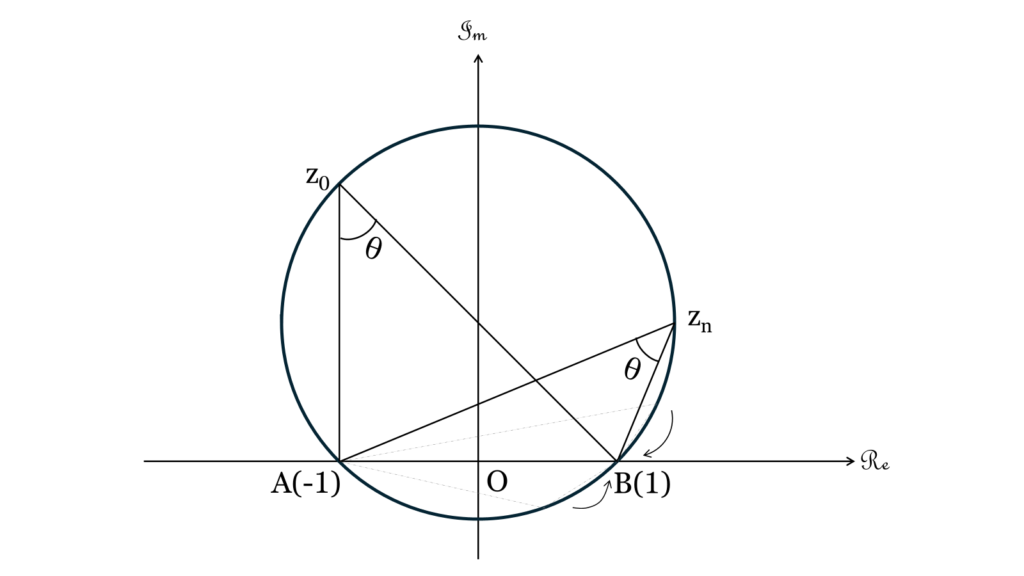
となり $z_n$ は $z_0$ と同じ偏角を取る。
よって円周角の定理から $z_n$ は3点 $(1),(-1),(z_0)$ で定まる円周上の点となり、 $n→∞$ のとき
$$\begin{align*} \left|\dfrac{z_n -1}{z_n +1}\right| &→0 \\ ∴z_n&→1 \end{align*}$$
となるから、 $z_n$ はやがてその円周上を点 $(1)$ に近づくことが分かる。
また一次分数変換によって $z_i,z_j,z_1,z_2$ がそれぞれ $w_i,w_j,w_1,w_2$ に変換されるとき、
$$
\dfrac{w -w_1}{w -w_2} = k \dfrac{z -z_1}{z -z_2}
$$
のように変換できることから、
$$\begin{cases}
\dfrac{w_i -w_1}{w_i -w_2} = k \dfrac{z_i -z_1}{z_i -z_2}\\
\dfrac{w_j -w_1}{w_j -w_2} = k \dfrac{z_j -z_1}{z_j -z_2}
\end{cases}$$
より
$$
\frac{z_i -z_1}{z_i -z_2} : \dfrac{z_j -z_1}{z_j -z_2}\\
= \dfrac{w_i -w_1}{w_i -w_2} : \dfrac{w_j -w_1}{w_j -w_2}
$$
が成り立つ。
つまり一次分数変換前後で一次分数変換の比の値が等しい(不動点が2個の場合)。
不動点が1個の場合
$c=0$ は一次分数関数にならないから論外として、$c≠0$ のとき、不動点が1個になる場合とは、
一次分数変換の不動点を求める方程式
$$\begin{align*}
&z = \dfrac{az-b}{cz-d} \\
&∴cz^2-(a-d)z-b = 0 \tag{★}
\end{align*}
$$
について $z$ が重解を持つ場合のことである。ただし2次方程式(★)の係数は複素数となる。
例えば一次分数変換
$$
w=\dfrac{z-4}{z-5}
$$
は不動点 $z=2$ のみを持つ。このときの複素数平面上における振る舞いを考えてみよう。
ここで不動点が1個の場合に以下のように変形できることを利用する。
$$
\dfrac{1}{w-α} =\dfrac{2c}{a+d} +\dfrac{1}{z-α} \tag{20}
$$
$$\begin{align*}
\dfrac{1}{w-2} &= \dfrac{2}{-4} +\dfrac{1}{z-2}\\
\dfrac{1}{w-2} &= -\dfrac{1}{2} +\dfrac{1}{z-2}\\
\end{align*}$$
この変形は不動点が1つ(重解)の場合にのみできるので、こちらも例により意欲のある読者は調べてほしい。なお(20)式のように変形できることの証明には不動点を求める方程式(★)が重解を持つような条件、つまりこの方程式(★)の判別式 $D$ が
$$
D=(a-d)^2+4bc=0
$$
となることを上手いこと利用する。
それでは以下の漸化式を複素数平面上で描画してみよう
例. ある $z_0$ が与えられている数列 $z_n(n\geq 0)$ が漸化式
$$
z_{n+1}=\dfrac{z_n-4}{z_n-5}
$$を満たすとき、この数列 $\{z_n \}$ の複素数平面上での振る舞いを調べる。
一次分数変換
$$
w=\dfrac{z-4}{z-5}
$$
は
$$
\dfrac{1}{w-2} = -\dfrac{1}{2} +\dfrac{1}{z-2}\\
$$
のように変形できるのであった。これを与えられた漸化式に当てはめると
$$
\dfrac{1}{z_{n+1}-2} = -\dfrac{1}{2} +\dfrac{1}{z_n-2}\\
$$
と変形できるから、この漸化式を満たす数列は
$$\begin{align} \dfrac{1}{z_n-2} &= -\dfrac{1}{2}n + \dfrac{1}{z_0-2} \\
∴ \{ζ_n\} &= -\dfrac{1}{2}n + ζ_0 \end{align} \tag{21}$$
となる。ただし $ζ_n = \dfrac{1}{z_n-2}$ と置いた。
よって(21)式は初項 $ζ_0$ の等差数列 $\{ζ_n\}$ であることが分かり、複素数平面上では $n$ が大きくなると実軸に平行に等間隔で $ζ_n$ を取る。ただし $z_0=2$ のとき(つまり初期値 $z_0$ が不動点となる場合)には特異点となり、このとき $|ζ_n|→∞$ となる。
従って数列 $\{z_n-2\}$ は(21)式の両辺の逆数を取ってあげれば良いので
$$
\{z_n-2\} =\hspace{1mm} – \dfrac{1}{\dfrac{1}{2}n – ζ_0} \tag{22}
$$
となる。
そこで数列 $\{z_n-2\}$ が複素数平面上でどのように描かれるのか見ていこう。
この数列は $n=2ζ_0$ のときに特異点となり、このとき分母は発散するので、 $|z_n-2|→0$ となる。つまり $z_0=2,n=2ζ_0$ となる場合には(22)式は発散してしまい $z_n$ の値がよく分からなくなるので、複素数平面上に描画するときにはこれらの場合を考慮しなければならないのだ。
右図は2つの数列 $\{ζ_n\},\{z_n\}$ が特異点を取らないような値を複素数平面上に図示した。数列 $\{z_n-2\}$ は複素数平面上において数列 $\{ζ_n\}$ の反転となるここで反転とは $n$ が等しい2つの複素数 $z_n-2, ζ_n$ はその偏角は実軸対象となり、これらの大きさの積は1となるような変換である。この反転を数列 $\{ζ_n\}$ に施すと、実部の符号を境に対象で虚軸に平行な半直線上を分布する。
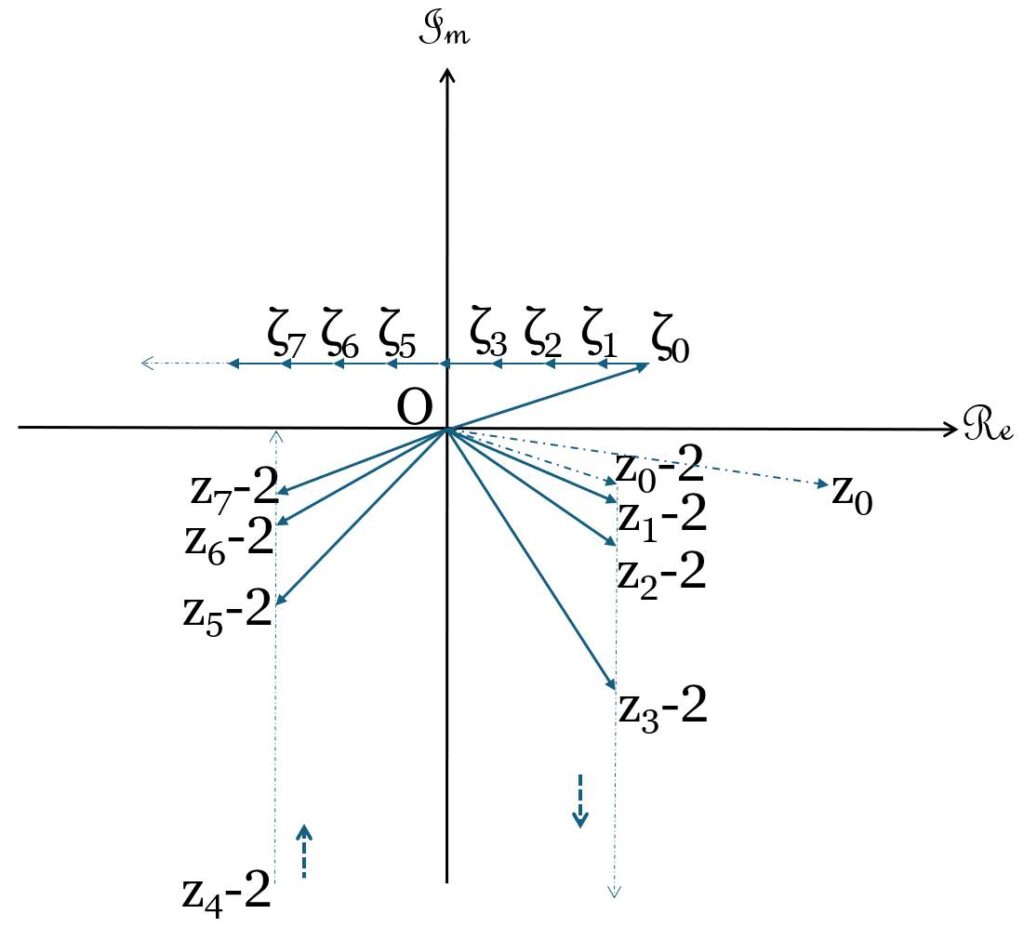
半直線上を分布
また以下複合同順で $ζ_n$ の実部が $0$ に近づく( $\Re(ζ_n) →±0$ )のとき $z_n-2→±∞$ となってしまいどちらの半直線上にあるのかよく分からない。よってこのときの $z_n-2$ は特異点と言える。
さて初項 $z_0$ を色々と動かしてみると、以下の特徴が現れるので確認していただきたい。
(1). 初項の虚部が正 $\Im(z_0) >0$ のときには、 $ζ_n$ の虚部は負( $\Im(ζ_n) <0$ )となる。
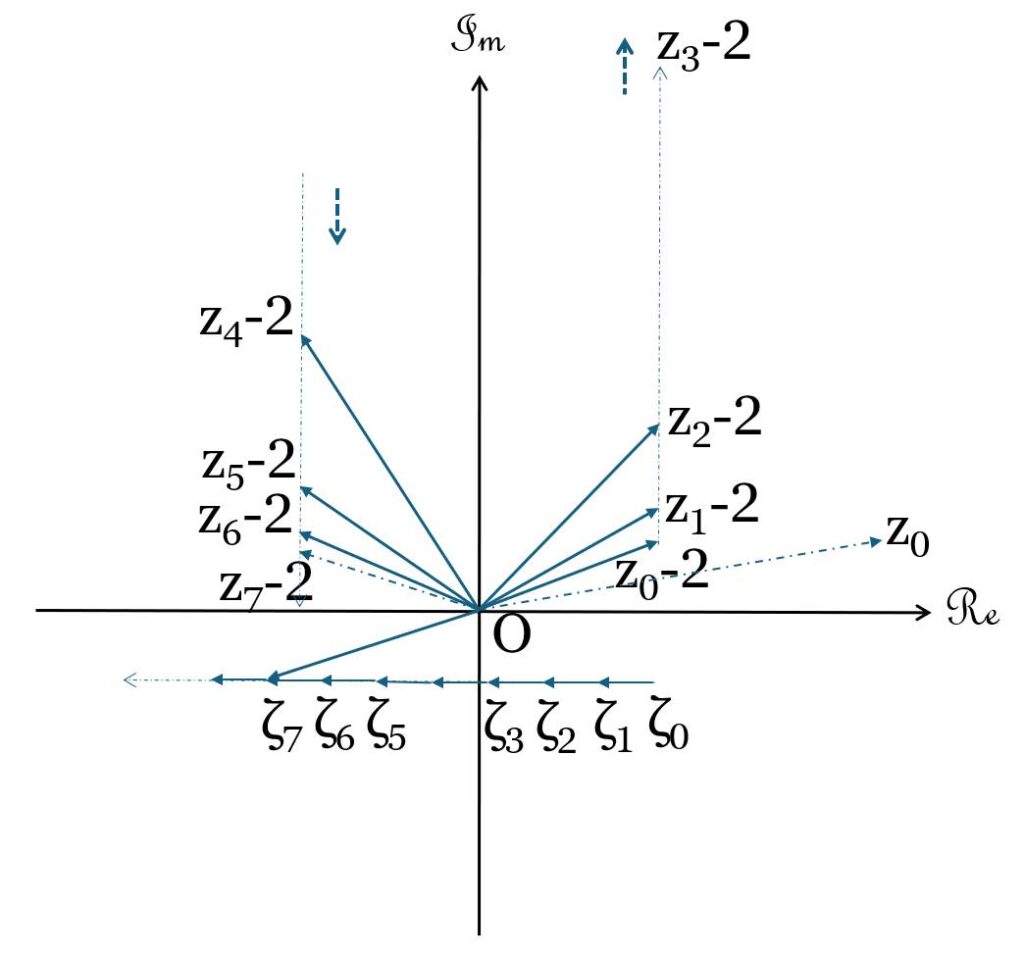
(2). 初項の実部が正( $\Re(z_0-2) <0$ )のときには、常に $ζ_n$ の実部は負( $\Re(ζ_n) <0$ )となるので、数列 $\{z_n-2\}$ の通る半直線は1つだけ存在する。
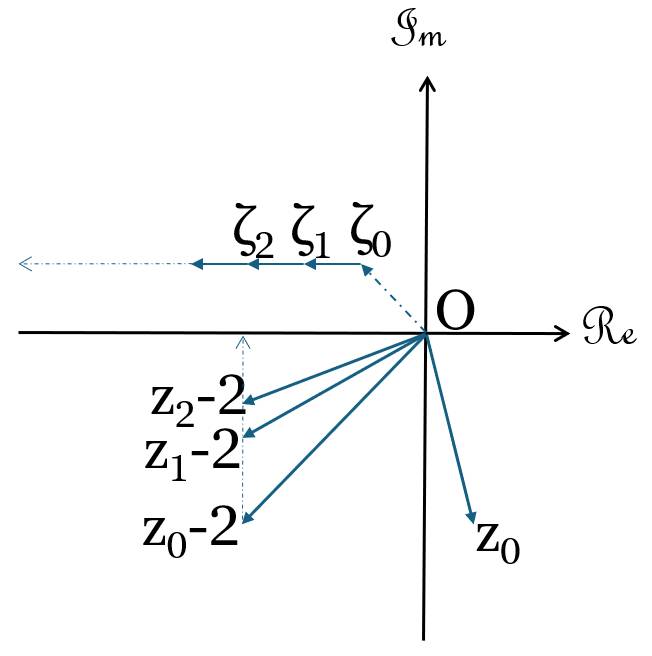
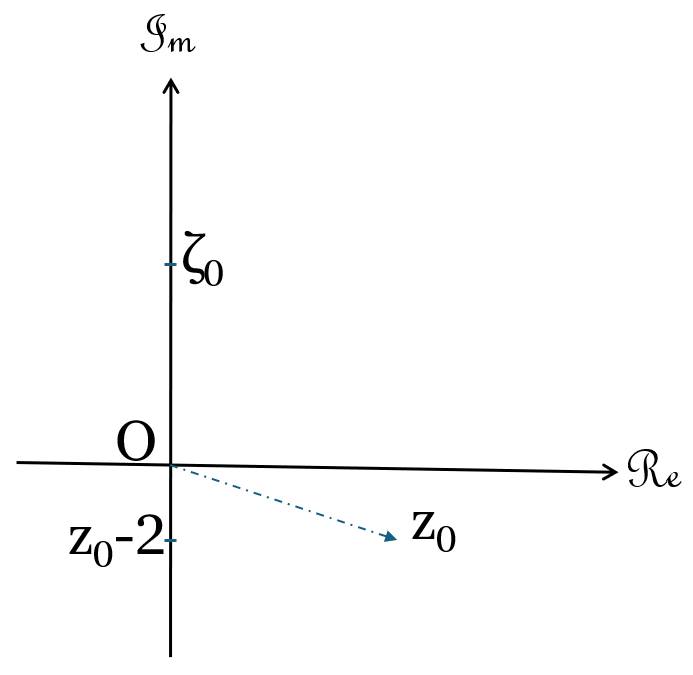
(3). やがて初項の実部が不動点に近づく( $\Re(z_0) →2±0$ )ときに、 $z_n-2$ は虚軸上を取る。
このときの数列 $\{ζ_n\}$ は偏角が $π/2$ となるが、そのような数列 $\{ζ_n\}$ は高々1点 $ζ_0$ のみである。そのため対応する数列 $\{z_n-2\}$ もまた1点 $z_0-2$ に決まる。
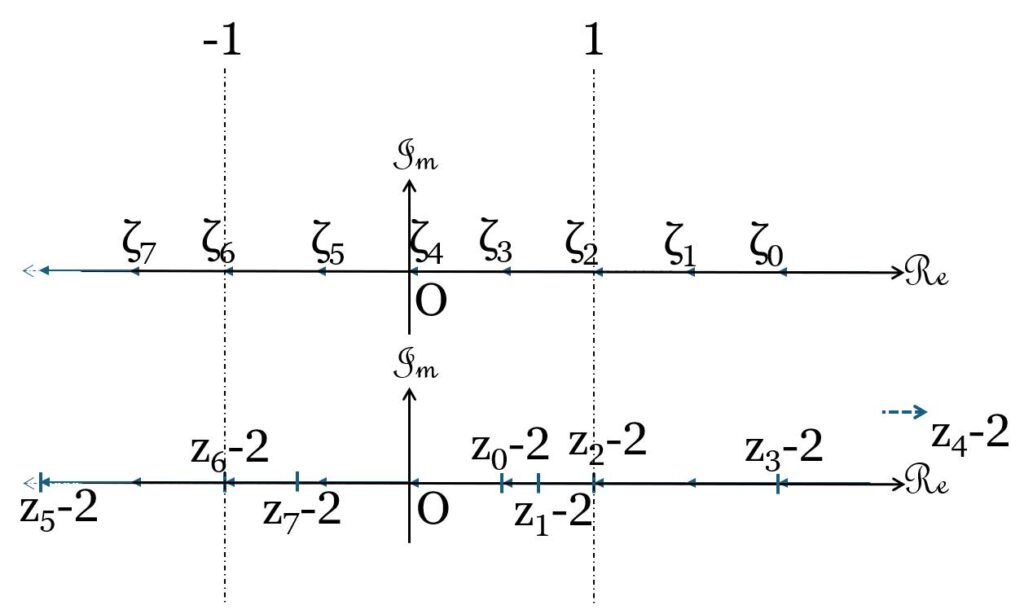
(4). 初項 $z_0$ を実軸に近づけると $ζ_n$ も実軸に近づき、やがて初項の虚部が $0$ に近づく( $\Im(z_0) →0$ )ときに $ζ_n$ は実軸上を取る。
このときの数列 $\{ζ_n\}$ は偏角が $0$ となるが、そのような数列 $\{ζ_n\}$ は $n$ の取りうる値によって存在する。そのため対応する数列 $\{z_n-2\}$ もまた $n$ の取りうる値によって存在するが、実軸上に分布する。また $n=2ζ_0$ となる $n$ が存在するとき、以下複合同順で $n→±0$ のとき $z_n-2→±∞$ となる。
このように一次分数で表現される比の値どうしの比を非調和比(複比)と言い、実は不動点の数に限らず一次分数変換の前後で非調和比は不変となので、次回簡単に証明してみよう。
ちょっと休憩
本記事では一次分数変換を複素数平面上で解析してみた。次回は一次分数関数から非調和比(複比)について解説していく。
初回
前回
次回



コメント