複素数平面における比の値の解釈

前書き

本記事はシリーズ『非調和比をそれっぽく解釈する』の第2部になります。

本記事では複素数平面における比の値について考察します。複素数平面とは複素数 $z$ を実部 $a$ と虚部 $b$ に分離し、実軸を横軸、虚軸を縦軸に取ったものです。複素数平面を用いると複素数の計算を図形的に解釈する他に、煩雑な操作を簡単に行うことができます。

本記事では複素数平面上の比の値が、どのような意味を持つのかを探求します。特に複素数 $b$ を複素数 $z$ によって複素数 $a$ に変換するという操作が、一次元 $\mathbb{C}$ 上の変換としてどのように解釈できるのかを考えます。

複素数平面における比の値

まず複素数平面において比の値

$$\begin{align} \dfrac{a}{b} &= z \\
∴a &= zb \end{align} \tag{5}$$

が何を意味しているのか考えてみる。

ここで複素数平面とは複素数 $z$ を実部 $a$ と虚部 $b$ に分離し実軸を横軸に取り虚軸を縦軸に取ったものである。複素数平面を用いれば恰も平面上の点 $(a,b)$ と見なせるだけでなく、複素数の諸計算を図形的に解釈することで煩雑な操作を簡単に施せるようになる。

例えば

$$\begin{cases}
a = x_a+y_ai \\
b = x_b+y_bi
\end{cases}$$

を

$$
\boldsymbol{a}=
\begin{pmatrix}x_a \\ y_a \end{pmatrix},
b=
\begin{pmatrix}x_b \\ y_b \end{pmatrix}
$$

と置くと、複素数平面上の複素数を $\mathbb{R}^2$ におけるある表現行列 $Z$ によって恰も線型変換

$$ \boldsymbol{a} = Z\boldsymbol{b} $$

という操作が可能なのである。

しかし実際には複素数 $b$ を複素数 $z$ によって複素数 $a$ に変換しているので、複素数 $z$ による変換とは一次元 $\mathbb{C}$ 上の変換である。よって一次元 $\mathbb{C}$ 上において

$$ a = zb \tag{5}$$

のような数同士の変換で書き表されるという制約が表現行列 $Z$ に掛かるはずだ。そこでその表現行列 Z がどのような制限を受けるのか見ていこう。

まず表現行列が単位行列 $I$ の場合には

$$\begin{align} \boldsymbol{a} &= \boldsymbol{b} \\
a &= 1・b \end{align}$$

となり、これは恒等変換となる。よって表現行列が単位行列の $r(∈\mathbb{R})$ 倍の場合には

$$\begin{align*} \boldsymbol{a} &= r\boldsymbol{b} \\
a &= rb \end{align*}$$

となり、複素数 $z$ は拡大・縮小（負の数の場合には反転）に作用する。よって表現行列 $Z$ の行列式の値を $r$ と置いて、行列式の値が $1$ となるような行列 $E$ を用いて

$$
|Z| = r = r|E| = |rE|
$$

と表わすことにすれば、表現行列 $Z$ の行列式の値 $r$ がそのまま複素数 $z$ において拡大・縮小に起因する $r$ となることが分かる。

さて複素数平面上を導入することで複素数は恰も $\mathbb{R}^2$ の座標系で考えることができるのだった。このことから複素数平面上において複素数 $z$ は円座標系における半径方向の基底 $\boldsymbol{e}_{r(φ)}$ を用いて

$$\begin{align*}
\boldsymbol{z}& = r\boldsymbol{e}_{r(φ)} \\
&= r
\begin{pmatrix} \cos φ \\
\sin φ \end{pmatrix}
\end{align*}$$

のように大きさ $r$ と偏角 $φ$ に依存する基底とで分離して書き表される。

よって複素数 $z$ は偏角 $φ$ を用いて

$$ z = r(\cos φ+i\sin φ) $$

のように書き表される。これは一般に複素数の極形式と呼ばれる表現だ。

或いは偏角 $α$ における半径方向の基底 $\boldsymbol{e}_{r(α)}$ と接線方向の基底 $\boldsymbol{e}_{φ(α)}$ の線型結合で表現すると

$$\begin{align*}
\boldsymbol{z} &= r((\boldsymbol{e}_{r(φ)}・\boldsymbol{e}_{r(α)})\boldsymbol{e}_{r(α)}+(\boldsymbol{e}_{r(φ)}・\boldsymbol{e}_{φ(α)})\boldsymbol{e}_{φ(α)})\\
&= r(\cos (φ-α)\boldsymbol{e}_{r(α)}+\sin (φ-α)\boldsymbol{e}_{φ(α)})
\end{align*}\tag{6}$$

となり、複素数は $\mathbb{R}^2$ の座標系において偏角 $α$ の複素数が $φ-α$ だけ回転することで偏角 $φ$ の複素数となることが分かる。

よって複素数 $z$ が偏角 $θ$ で表されている場合には

$$\begin{align} a = zb = r(\cos θ+i\sin θ)b \tag{7} \end{align}$$

という変換は、複素数 $b$ を $r$ 倍に拡大して偏角 $θ$ だけ回転させることを意味する。

故に $\mathbb{R}^2$ の座標系で表現行列 $E$ に相当するような行列は回転行列

$$\begin{pmatrix}
\cos θ && -\sin θ \\
\sin θ && \cos θ
\end{pmatrix} \tag{8}$$

となる。

従って2次元平面のデカルト座標系における点を複素数平面上の点に対応させたとき、この点に(7)式 $z=r(\cos θ+i\sin θ)$ を作用させて得られる複素数は、 $r$ だけ拡大され $θ$ だけ回転されたものになる。ここで得られた複素数はそのまま2次元平面のデカルト座標系における点に対応する。

例えば点 $(1,2)$ を $2$ 倍して $π/6$ だけ回転させた点は以下のように求められる。

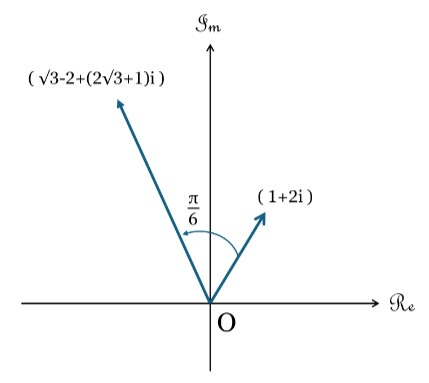
従って複素数平面において比の値

$$
\dfrac{a}{b} = z = r(\cos θ+i\sin θ)
$$

は、複素数 $b$ から複素数 $a$ に遷移するのにどれだけ拡大し回転するのかを表わす。また2次元平面のデカルト座標系の場合に限定されるが、複素数平面における比の値を用いることで、拡大や回転等の変換は数同士の比の値として一次元複素数体 $\mathbb{C}$ 内で処理することができる。

よって複素数を掛けるということは、 $\mathbb{R}^2$ の座標系においては線型変換に対応していると言える。

ちょっと休憩

本記事では複素数平面上における比の値を解析してみた。次回は比の値から一次分数変換について複素数平面上で考察していこうと思う。