初めに
法線ベクトルとは、ある曲線や曲面上の点においてその点での接線に直交するベクトルのことを指します。接線ベクトルと同様に法線ベクトルもその点での微分幾何学の概念であり、その点での曲線や曲面の局所的な性質を表すことができます。
一般的に曲面上の点における法線ベクトルは、その点での曲面の勾配ベクトル(法線方向に最も急な方向を表すベクトル)を表します。勾配ベクトルはベクトル解析において勾配演算子($\nabla$)を用いて表現され、勾配演算子を曲面の方程式に適用することで求めることができます。
また曲線上の点における法線ベクトルは、その点での曲線の接線ベクトルに直交するベクトルとして定義されます。これは曲線上の点での接線ベクトルが曲線の傾きを表すため、傾きに直交するベクトルが法線ベクトルとなるからです。
本記事ではこの事実を数式を交えて解説していきます。
ナブラ $\nabla$ についてはこちらの記事
を参照してください。
法線ベクトルとは何か
2つのベクトル $\overrightarrow{OA},\overrightarrow{AP}$ が直交しているということは、2つのベクトルが独立であるということから内積を用いて
$$\overrightarrow{OA}\cdot\overrightarrow{AP}=0 \tag{1}$$
と表現できる。内積についてよく分からない読者は
を参照するように。
勿論2つのベクトル $\overrightarrow{OA},\overrightarrow{AP}$ は始点と終点を固定された定ベクトルとしても良いが、本記事ではこれらのベクトルを関数として考えてみる。
さて原点 $O$ と2点 $A(x_0,y_0),P(x,y)$ ($x,y$ は変数) によって2つのベクトル $\overrightarrow{OA},\overrightarrow{AP}$ を
$$\begin{cases}
\overrightarrow{OA}=(x_0,y_0)\\
\overrightarrow{AP}=(x-x_0,y-y_0)
\end{cases} \tag{2}$$
と定義する。するとベクトル $\overrightarrow{AP}$ は動点 $P(x,y)$ を終点にもつベクトル関数となる。このベクトル関数という表現は、2つの変数 $x,y$ が独立変数(互いに関与しない変数)であっても良いが、当然これらの変数 $x,y$ が関数 $f_{(x,y)}=0$ という依存性を持っていても良いという意味である。つまりベクトルを成す成分が関数であることもあるということである。今は一旦は2つの変数 $x,y$ の依存性を考慮せずに考えていこう。
円の接線と法線ベクトル
2つのベクトル $\overrightarrow{OA},\overrightarrow{AP}$ が直交するときには内積(1)式を計算すると
$$\begin{align*}
\overrightarrow{OA}\cdot\overrightarrow{AP}&=0\\
∴ x_0(x-x_0)+y_0(y-y_0)&=0\\
∴ x_0x+y_0y&=x_0^2+y_0^2 \tag{3}
\end{align*}$$
となる。得られた(3)式は2つの変数 $x,y$ が満たすべき関係式であり、右辺はベクトル $\overrightarrow{OA}$ の大きさを表している。左辺は当然ながら2つのベクトル $\overrightarrow{OA},\overrightarrow{OP}$ の内積となっている。よってこの大きさを $r$ と置くと、(3)式は
$$\begin{align*}
x_0x+y_0y&=r^2\\
∴ \overrightarrow{OA}\cdot\overrightarrow{OP}&=|\overrightarrow{OA}|^2
\end{align*} \tag{4}$$
と書き表される。この $r$ とは定点 $A(x_0,y_0)$ の距離とも解釈できる。ところで(3)式の右辺を
$$x_0^2+y_0^2=|\overrightarrow{OA}|^2=r^2$$
と置いたが、 $r^2=Const.$ を満たすように2つの変数 $s,t$ を用いて
$$s^2+t^2=r^2 \tag{5}$$
と置くと、(5)式は原点を $O$ とする半径 $r$ の円となる。
よって(4)式で表現される式とは方程式
$$x^2+y^2=r^2$$
で表現される原点 $O$ を中心とする半径 $r$ の円周上の点 $A(x_0,y_0)$ における接線の方程式
$$x_0x+y_0y=r^2 \tag{4}$$
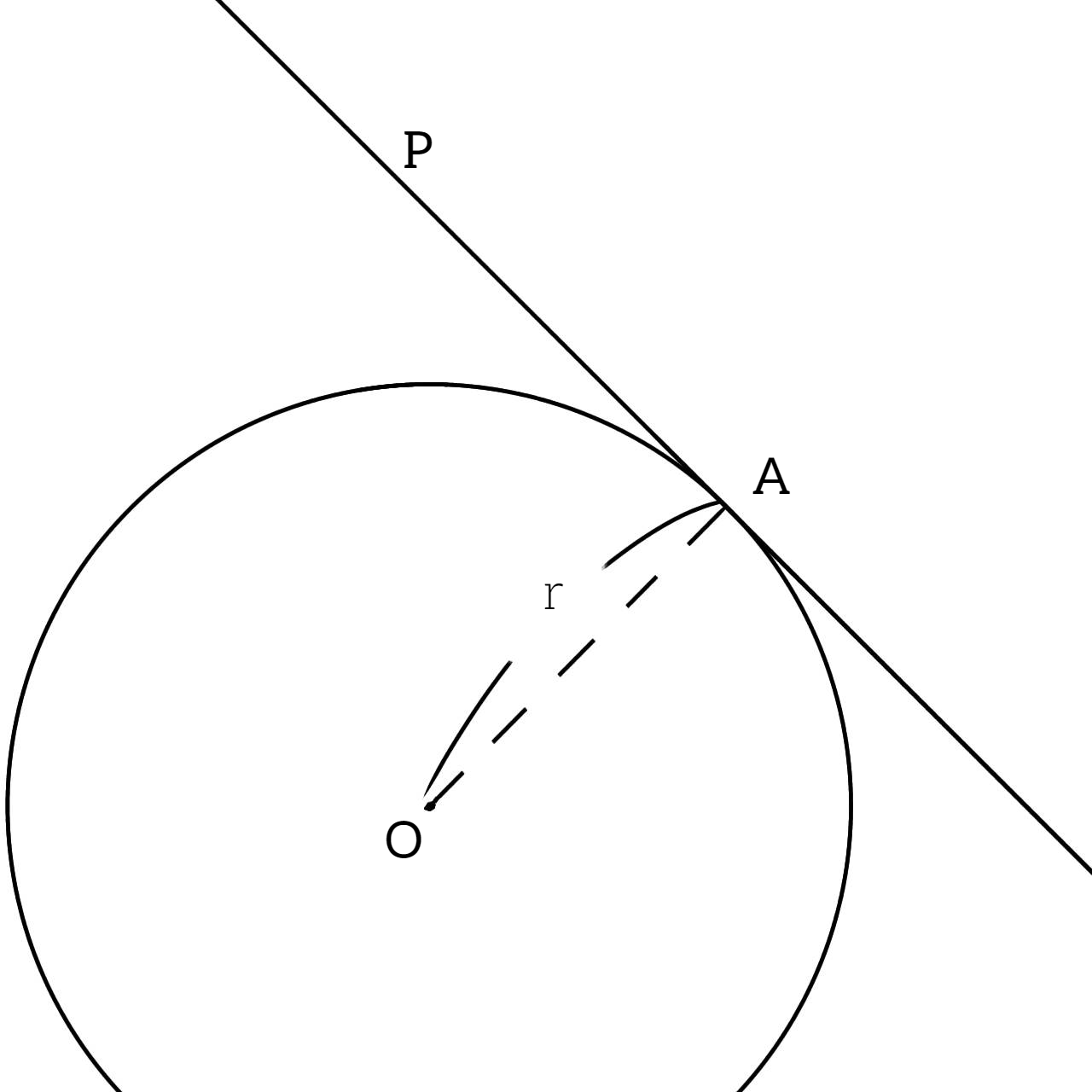
であることが分かる。これは原点 $O$ を中心としているが、2点 $A(x_0,y_0),P(x,y)$ 以外の任意の点 $B(a,b)$ を中心とするのであれば、(4)式は
$$\begin{align*}
\overrightarrow{BA}\cdot\overrightarrow{BP}&=|\overrightarrow{BA}|^2\\
∴ (x_0-a)(x-a)+(y_0-b)(y-b)&=r^2
\end{align*} \tag{6}$$
のように表される。
(4)、(6)式は点 $P(x,y)$ が満たすべき直線の方程式である。このとき2つのベクトル $\overrightarrow{OA},\overrightarrow{BA}$ はそれぞれの直線に対しての法線ベクトルとなる。つまり直線の方程式
$$ax+by=c$$
について、この直線の法線ベクトル $\vec{n}$ の1つは $\vec{n}=(a,b)$ なのである。
曲面の法線ベクトルと接平面の解析
曲面と曲線の方程式
そこで(1)式
$$\overrightarrow{OA}\cdot\overrightarrow{AP}=0 \tag{1}$$
のベクトル $\overrightarrow{OA}$ を形成する変数 $x,y$ が関数 $z=f_{(x,y)}$ を用いて $f_{(x,y)}=0$ という依存性を持っているような場合について考えてみる。つまり今まで考えてきた定点 $A(x_0,y_0)$ の各成分を変数 $x,y$ とするのである。ここで関数 $z=f_{(x,y)}$ とは変数 $z$ を2変数で表現している。このことから3次元ユークリッド空間におけるデカルト座標系 $(x,y,z)$ では、関数 $z=f_{(x,y)}$ で定義される $z$ は曲面を表す。よって $f_{(x,y)}=0$ で表現される図形とは、 $z=f_{(x,y)}$ を $z=0$ の平面(つまり $xy$ 平面)で切り取った図形となるのだ。
例えば曲面
$$z=f_{(x,y)}=x^2+y^2$$
を $z=4$ の平面で切り取ると、この平面上では曲面 $z$ は原点を中心とする半径2の円となる。もしくはこの関数 $f_{(x,y)}$ を $z$ 方向に-4だけ平行移動させたもの
$$\begin{align*}
z-(-4)&=f_{(x,y)}\\
∴ z&=x^2+y^2-4
\end{align*}$$
を平面 $z=0$ で切り取った場合と考えても良い。
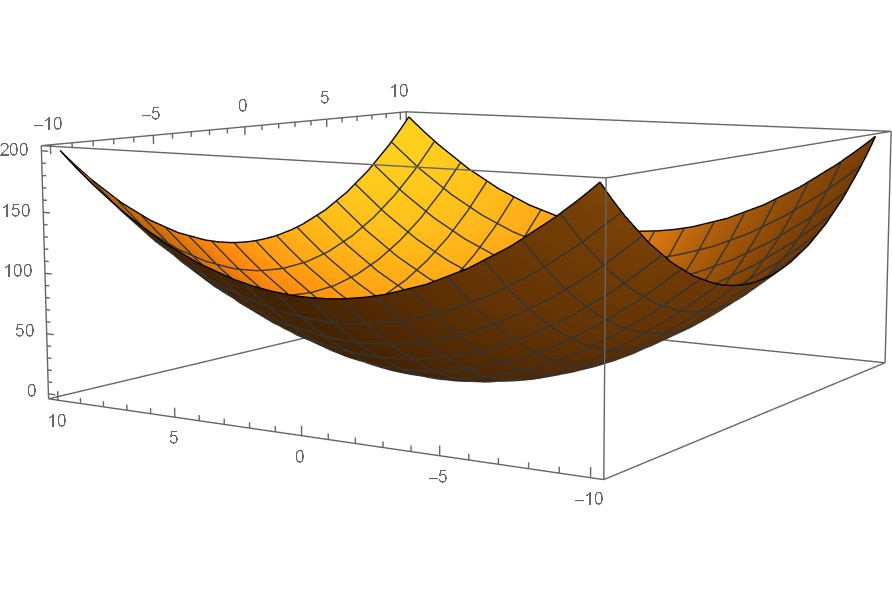
接平面を成す接ベクトルの基底
それでは曲面 $z=f_{(x,y)}$ のある点 $A(x,y)$ についてベクトル $\overrightarrow{OA}$ に直交する接平面 $α$ を考えよう。この接平面 $α$ 上に含まれるベクトル $\overrightarrow{AP}$ について考えることは、 $xy$ 平面では接ベクトル $\overrightarrow{AP}$ を考えることに該当する。
接平面 $α$ 上に含まれるベクトル $\overrightarrow{AP}$ は平面上のベクトルであるから、2つの基底により表現することが可能である。そこで接平面 $α$ 上にある2つの基底 $\langle \boldsymbol{e}_u,\boldsymbol{e}_v\rangle$ を用いて
$$\overrightarrow{AP}=u\boldsymbol{e}_u+v\boldsymbol{e}_v \tag{7}$$
のように表すことにする。
ここで任意のベクトル $\overrightarrow{AP}$ は単一の単位ベクトル $\boldsymbol{e}_{α{(u,v)}}$ によって
$$\overrightarrow{AP}=t\boldsymbol{e}_{α(u,v)} \tag{8}$$
と表されることに注意する。ただし単位ベクトル $\boldsymbol{e}_{α(u,v)}$ は
$$\boldsymbol{e}_{α(u,v)}=\dfrac{1}{\sqrt{u^2+v^2}} (u\boldsymbol{e}_u+v\boldsymbol{e}_v) \tag{9}$$
として書き表され、変数 $u,v$ の取りうる値によって変化する。これは当たり前のことではあるが、ベクトル $\overrightarrow{AP}$ は接平面 $α$ 上に含まれることから、2つの変数 $u,v$ の値が定まれば $t$ はベクトル $\overrightarrow{AP}$ の方向ベクトルを常に一定の向きにさせるような値を取る(つまり2つの変数 $u,v$ に依存しない定数となる)。
ここで(9)式から接平面 $α$ 上のベクトル $\overrightarrow{AP}$ を成す単位ベクトル $\boldsymbol{e}_{α{(u,v)}}$ とは、
$$\begin{align*}
\boldsymbol{e}_{α(u,v)}&=\dfrac{1}{\sqrt{u^2+v^2}} (u\boldsymbol{e}_u+v\boldsymbol{e}_v) \tag{9}\\
∴ \boldsymbol{e}_{α_{(l;u,v)}}&=l_{(u,v)}\boldsymbol{e}_{l{(u,v)}} \tag{10}
\end{align*}$$
のように2つの変数 $u,v$ に依存する関数 $l_{(u,v)}$ と、接平面 $α$ 上のベクトル $\overrightarrow{AP}=(u,v)$ における方向ベクトル $\boldsymbol{e}_{l{(u,v)}}=\langle \boldsymbol{e}_u,\boldsymbol{e}_v\rangle$ とで分離することができる。後者で単位ベクトル $\boldsymbol{e}_{α{(l;u,v)}}$ の方向を定め、前者で規格化をしているのである。
曲面を介したベクトルの解析
次に関数 $z=f_{(x,y)}$ で表される曲面について考える。今までの考察から接平面 $α$ 上の点 $\overrightarrow{OP}$ はこの曲面上の点 $\overrightarrow{OA}$ を介して
$$\begin{align*}
\overrightarrow{OP}&=\overrightarrow{OA}+\overrightarrow{AP}\\
\overrightarrow{OP}&=(x\boldsymbol{e}_x+y\boldsymbol{e}_y)+t(l\boldsymbol{e}_{l(u,v)})
\end{align*}$$
と表現される。ここで注意したいのは2つのベクトル $\overrightarrow{OA},\overrightarrow{AP}$ の単位ベクトルは独立であるということである。これは定義(1)式
$$\overrightarrow{OA}\cdot\overrightarrow{AP}=0 \tag{1}$$
により明らかである。そのためベクトル $\overrightarrow{OA}$ は単純に単位ベクトル
$$\boldsymbol{e}_{f{(x,y)}}=\dfrac{1}{\sqrt{x^2+y^2}} (x\boldsymbol{e}_x+y\boldsymbol{e}_y)$$
を用いて
$$\overrightarrow{OA}=r\boldsymbol{e}_{f{(x,y)}} \tag{11}$$
と表すと、ベクトル $\overrightarrow{OP}$ は
$$\begin{align*}
\overrightarrow{OP}&=r\boldsymbol{e}_{f{(x,y)}}+t\boldsymbol{e}_{α{(l;u,v)}}\\
&=(r,t)
\end{align*} \tag{12}$$
のように正規直交基底 $\langle \boldsymbol{e}_{f{(x,y)}},\boldsymbol{e}_{α{(l;u,v)}}\rangle$ を用いることで2次元で表現することができるのである。よってベクトル $\overrightarrow{OA}$ は $l_{(u,v)};u,v$ に依存しないことから
$$\dfrac{df_{(x,y)}}{dl}=0$$
或いは
$$\dfrac{∂f_{(x,y)}}{∂u}+\dfrac{∂f_{(x,y)}}{∂v}=0$$
となる。特に後者の式は微分作用素
$$\nabla_{u,v}:=\dfrac{∂}{∂u}\boldsymbol{e}_u+\dfrac{∂}{∂v}\boldsymbol{e}_v$$
を用いて
$$\begin{align*}
\dfrac{∂f_{(x,y)}}{∂u}+\dfrac{∂f_{(x,y)}}{∂v}&=\dfrac{∂f_{(x,y)}}{∂u}(\boldsymbol{e}_u\cdot\boldsymbol{e}_u)+\dfrac{∂f_{(x,y)}}{∂v}(\boldsymbol{e}_v\cdot\boldsymbol{e}_v)\\
&=\left(\dfrac{∂}{∂u}\boldsymbol{e}_u+\dfrac{∂}{∂v}\boldsymbol{e}_v\right)f_{(x,y)}\cdot(\boldsymbol{e}_u+\boldsymbol{e}_v)=0\\
&∴ \nabla_{u,v}f_{(x,y)}\cdot l_{(1,1)}\boldsymbol{e}_{l{(1,1)}}=0\\
&∴ \nabla_{u,v}f_{(x,y)}\cdot\boldsymbol{e}_{α{(l;1,1)}}=0 \tag{13}
\end{align*}$$
となる。ただし
$$\boldsymbol{e}_{α_{(l;1,1)}}=l_{(1,1)}\boldsymbol{e}_{l{(1,1)}} \tag{10}$$
とした ($u,v=1$) 。よって $z=f_{(x,y)}$ で表現される曲面の勾配 $\nabla f_{(x,y)}$ は(13)式より接平面 $α$ に垂直なベクトル(法線ベクトル)になる。特に
$$z=f_{(x,y)}=c$$
のように $z$ が定数 $c$ と置かれる場合には、曲面 $z=f_{(x,y)}$ は曲線となり、法線ベクトルは $xy$ 平面上にあるのだ。従って右辺を0に置き直した曲線 $f_{(x,y)}=0$ の勾配 $\nabla f_{(x,y)}$ は曲線 $f_{(x,y)}=0$ の法線ベクトルを得る。
最後に
本記事では勾配 $\nabla f_{(x,y)}$ が曲面、曲線の法線ベクトルとなることを数式を交えて解説した。そのために接平面 $α$ を成す基底を定義したりとかなり抽象的な内容であったのかもしれない。本記事では3次元ユークリッド空間で議論しているが、この考え方は多次元にも適用される。その場合には上手い具合に各基底を多変数に依存するように定義してあげれば、超曲面上のベクトル $\overrightarrow{OA}$ と超接平面 $α$ 上のベクトル $\overrightarrow{AP}$ を考えることになるが、結局基底による議論なので本記事での議論に帰着するのだ。



コメント