内積の定義
「内積とは何か」これはよくある質問である。
高校では $n$ 次元ベクトルと言えばただ次の2式
$$\vec{a}\cdot\vec{b} = \sum_{i=1}^na_{i}b_{i} \tag{1}$$
$$\vec{a}\cdot\vec{b} = |\vec{a}||\vec{b}|\cos θ \tag{2}$$
で定義されるだけである。そりゃ何が何だか分からないわな。
まずそもそも内積とは実ベクトル空間だけで定義される計量ではない。高校数学では実ベクトル空間の更に幾何ベクトルしか扱われないため、内積と言えば実ベクトルの内積とされる。
結論として内積に数学的な意味を持たせるのなら、それは2つのベクトル(または関数)の従属度合いに依存した掛け算である。(1)式を見ればその理由は見えてきそうである。同じ成分同士を掛けたものを合わしている。
(1)は各成分の積を足している。(2)はまあ幾何ベクトルで視覚的な理解のためには必要であるが、しょっちゅう抽象化する数学においては応用が利きにくい。
実は複素 $n$ 次元ベクトルでの内積(エルミート積)の定義は(1)と類似していて
$$\langle\boldsymbol{a},\boldsymbol{b}\rangle=\boldsymbol{a^*}\cdot\boldsymbol{b} = {}^t\boldsymbol{\bar{a}}\cdot\boldsymbol{b}=\sum_{i=1}^n a_{i}b_{i} \tag{3}$$
と表される。ただし $\boldsymbol{a}$ は列ベクトル $\vec{a}$ のことである。太文字にしたのは図形的な性質を剥いだ(つまり→で表されない)一般的なベクトルを指しているからである。 $\boldsymbol{a^*} = {}^t\boldsymbol{\bar{a}}$ は $\boldsymbol{a}$ の複素共役転置行列(随伴行列)であり、 ${}^t\boldsymbol{a}$ は $\boldsymbol{a}$ の転置行列、 $\boldsymbol{\bar{a}}$ は $\boldsymbol{a}$ の複素共役行列となる。列ベクトルの転置後は行ベクトルとなることに注意されたい。
「従属度合い」の解釈
(1)式や(3)式を見れば明らかではあるが、私が言う従属度合いとは各成分がどれだけ重なるのかを計量化したもののことを指す。
例えば幾何ベクトルで平行というのは従属度合いが最大(又は最小)である。つまり内積 $\langle\boldsymbol{a},\boldsymbol{b}\rangle$ の大きさは $|\boldsymbol{a}||\boldsymbol{b}|$ となる。これは数の掛け算の大きさ $|a \cdot b|$ に等しい。つまり1次元の数ベクトルと見なせる。
同様に垂直と言えば従属度合いが0である。つまり内積 $\langle\boldsymbol{a},\boldsymbol{b}\rangle$ も当然0である。だから2つのベクトルが直交しているかの判定によく使われているのである。
単位ベクトルが正規直交基底でない場合
今までの話は全て正規直交系でのお話である。正規直交系とは例えばデカルト座標系や極座標系のことを指す。この座標空間内のベクトルは全て先述の内積の式が成り立つ。
しかしこれでは非正規直交系(斜交座標等)では使い物にならない。そこでベクトルを単位ベクトル $\boldsymbol{e}_{n}$ の線形結合で表して、ベクトルの内積を次の式
$$\langle\boldsymbol{a},\boldsymbol{b}\rangle \equiv \sum_{i=1}^n a_{i}\boldsymbol{e}_{i} \cdot \sum_{j=1}^nb_{j}\boldsymbol{e}_{j} = \sum_{i=1}^n\sum_{j=1}^n a_{i}b_{j}\langle\boldsymbol{e}_{i} , \boldsymbol{e}_{j}\rangle \tag{4}$$
のように各単位ベクトル $\boldsymbol{e}_{n}$ 同士の積で表すことにする。すると、正規直交系では規格化直交条件
$$\langle\boldsymbol{e}_{i},\boldsymbol{e}_{j}\rangle=δ_{ij} \tag{5}$$
を満たす( $δ_{ij}$ はクロネッカーのデルタで、 $i=j$ のときには $δ_{ij}=1$ となり、 $i\neq j$ のときには $δ_{ij}=0$ となる)から、結局(3)式に辿り着く。
内積の使い道
ベクトルが正規直交基底の線形結合で表されている場合には内積の恩恵が感じられにくいが、内積を $\langle\boldsymbol{a},\boldsymbol{b}\rangle$ のように置き、具体的な計算を避けることで議論を進めることができる。この形式はエルミート積やエルミート半双線型形式などと呼ばれる。ここでは詳しい言及は避けるが、その性質から量子力学で役に立つ。
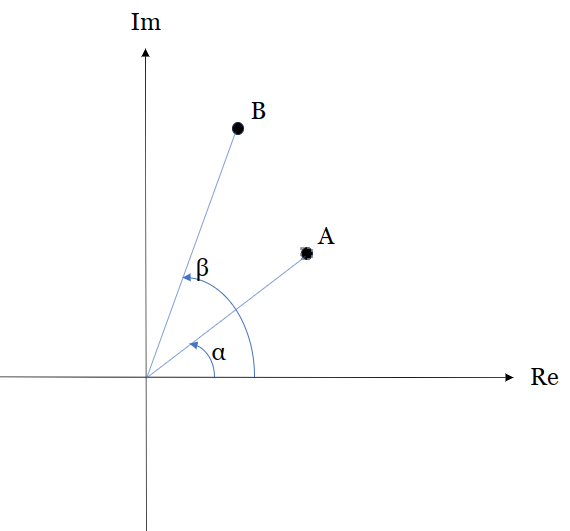
複素数平面上におけるエルミート積の表現
複素1次元数ベクトルのエルミート積を複素数平面上に図示してみよう。
$φ=\arg\angle{AOB}=β-α$ の2つの複素1次元数ベクトル $\boldsymbol{a},\boldsymbol{b}$ について先のエルミート積の定義から
$$\langle\boldsymbol{a},\boldsymbol{b}\rangle= |\boldsymbol{a}||\boldsymbol{b}|e^{iφ} \tag{6a}$$
$$\langle\boldsymbol{b},\boldsymbol{a}\rangle= |\boldsymbol{b}||\boldsymbol{a}|e^{-iφ} \tag{6b}$$
となる。
この結果を用いることで複素数平面の諸々の公式や条件式を解析的に導出することができる。
例えば $φ=π/2$ のときには
$$\langle\boldsymbol{a},\boldsymbol{b}\rangle= |\boldsymbol{a}||\boldsymbol{b}|\cdot i \tag{7a}$$
$$\langle\boldsymbol{b},\boldsymbol{a}\rangle= |\boldsymbol{b}||\boldsymbol{a}|\cdot (-i)\tag{7b}$$
となり、(7a)÷(7b)より
$$\frac{\langle\boldsymbol{a},\boldsymbol{b}\rangle}{\langle\boldsymbol{b},\boldsymbol{a}\rangle}=-1 \tag{8}$$
$$∴\langle\boldsymbol{a},\boldsymbol{b}\rangle+\langle\boldsymbol{b},\boldsymbol{a}\rangle=0 \tag{9}$$
これは複素数平面でよく出てくる条件式である。複素数平面とは複素1次ベクトルを平面に図示したものなので、当たり前と言えば当たり前なのだ。
因みに途中ででてきた $e^{iφ}$ はかの有名なオイラーの公式
$$e^{iφ}=\cosφ+i\sinφ$$
を適用させれば実部は内積っぽくなり、虚部は外積っぽくなる( $φ$ とは複素数平面における位相差のことなので、各項自体は内積でも外積でもないのは言うまでもないか)。
よってより一般的な複素 $n$ 次ベクトルの場合にはエルミート積は各次元における位相差 $φ_j$ を用いて
$$\begin{align*}
\langle a,b\rangle&= \sum_{j=1}^n \bar{a}^jb_je^{iφ_j}\\
&= \sum_{j=1}^n \bar{a}^jb_j(\cos φ_j+i\sin φ_j)
\end{align*}\tag{10}$$
と表される。なお $a^jb_j$ はアインシュタインの縮約記法を用いた。
終わりに
今回は高校数学で学ぶ内積を少し詳しく書いてみた。エルミート積の性質やベクトル空間などについて説明すると、大学数学の代数学に足を突っ込むことになる。ここでは高校数学を学習した人に数学の面白さを知ってもらうことが目的であるためこれ以上の説明はここでは控える。そのためこの記事を読んでもっと知りたいと思ってくれた人には是非その意欲を捨てずに学習していってほしい。本ブログにもいずれ書き込むつもりではあるが待たずに勉強してくれると非常に嬉しい。
高校数学ではタブー視されている外積について紹介している記事。



コメント