この記事は
の続きとなっている。式番号はこちらから続いているので、まだ見ていない読者はこちらから参考にされたい。
逆三角関数と逆双曲線関数と複素対数関数
逆三角関数、逆双曲線関数とは
関数 $y=f(x) $ が全単射となるときには関数の変数 $x,y$ を入れ替えた $x=f(y)$ が存在する。これを $y=g(x)$ のように変形したときに $g(x)$ を関数 $f(x)$ についての逆関数と言い、これを $f^{-1}(x)$ と書く。
三角関数や双曲線関数も同様に逆関数
$$\sin^{-1} x \cos^{-1} x \tan^{-1} x$$
$$\sinh^{-1} x \cosh^{-1} x \tanh^{-1} x$$
が存在し、それぞれ逆三角関数、逆双曲線関数と呼ばれる。ただしこれらは-1乗された関数(割関数)
$$(\sin x)^{-1} (\cos x)^{-1} (\tan x)^{-1}$$
$$(\sinh x)^{-1} (\cosh x)^{-1} (\tanh x)^{-1}$$
と混合を防ぐため、しばしば
$$\arcsin x \arccos x \arctan x$$
$$\text{arsinh}\hspace{1mm} x \text{arcosh}\hspace{1mm} x \text{artanh}\hspace{1mm} x$$
等と書かれる。しかし三角関数については逆関数という性質上実数の範囲で全単射となるように主値を取らなければならず、更にこれらと区別するために左端を大文字にして
$$\text{Arcsin}\hspace{1mm} x \text{Arccos}\hspace{1mm} x \text{Arctan}\hspace{1mm} x$$
と書かれたりする。この慣習は対数関数 $\log x$ でも使われる。以降このブログで左端が大文字になっている関数があれば、それは主値を取っているものだと思われたい。
$\cosh x$ は全射ではないため、その逆関数 $\text{Arcosh}\hspace{1mm} x$ の定義域は制限される。更に $\cosh x$ は単射ではないため、$\cosh x$ の $x<0$ の部分はその逆関数 $\text{Arcosh}\hspace{1mm} x$ の $y<0$ に反映されない。これは逆割双曲線関数 $\text{Arcsech}\hspace{1mm} x$ の場合も同様である。
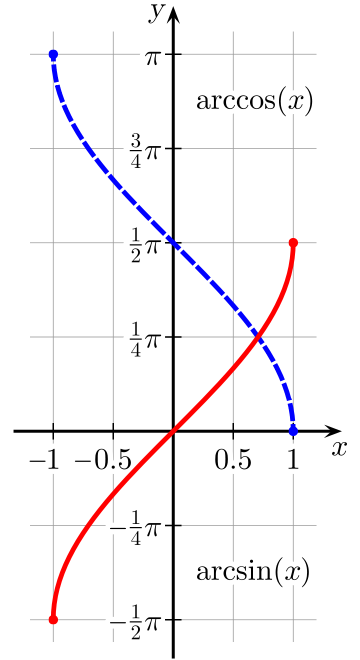
出典:Wiki
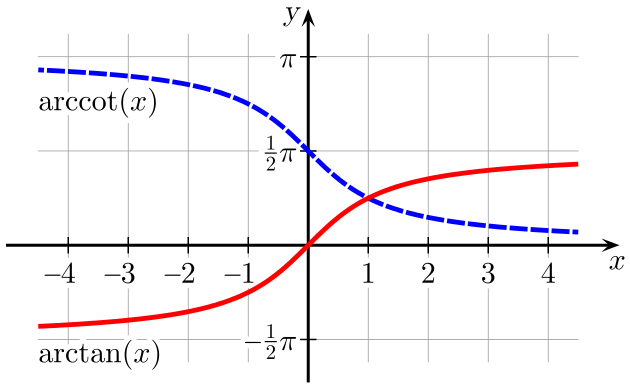
出典:Wiki
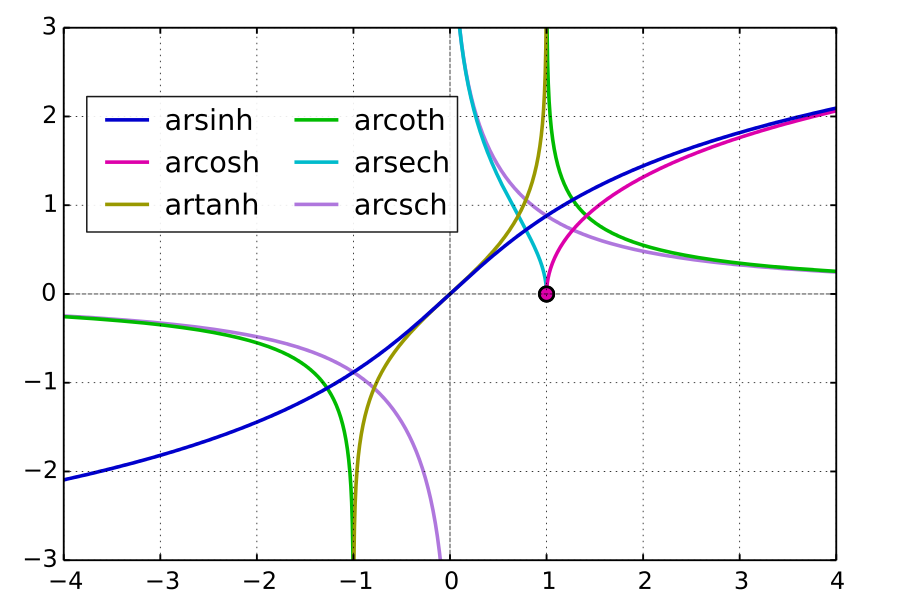
出典:Wiki
複素対数関数とは
三角関数、双曲線関数の複素指数関数表示で現れたように、指数関数は複素数の情報を取り入れることで三角関数の性質を持つことが分かった。ここでは更に変数 $x$ を一般の複素数 $z=x+iy$ に拡張すると
$$z=x+iy=e^{\text{Log}\hspace{1mm} z}=e^{\log |z|+iθ}=|z|e^{iθ} \tag{13}$$
と表されることに注目したい。ただし $θ$ は複素数 $z$ の偏角 $\text{Arg}\hspace{1mm} z$ とし、途中の $\text{Log}\hspace{1mm} z$ は
$$\text{Log}\hspace{1mm} z=\log |z|+iθ=\log |z|+i\text{Arg}\hspace{1mm} z \tag{14}$$
を満たすものとする。先に述べた通り当然これは主値を表すものであり、一般の場合には $e^{iθ}$ が $2π$ 周期であることから
$$\log z=\log |z|+i\text{Arg}\hspace{1mm} z+2nπi=\log |z|+\arg z \tag{15}$$
と書き表される。高校数学では対数関数と言えば(14)式の特に $\arg z(=θ)=0,n=0$ のときに限定されていたのである。
複素対数関数による逆三角関数、逆双曲線関数の表現
前回の記事三角関数、双曲線関数の複素指数関数表示で先述した通り、
$$\begin{cases} \cosθ=\frac{e^{iθ}+e^{-iθ}}{2}\\
\sinθ=\frac{e^{iθ}-e^{-iθ}}{2i}
\end{cases} \tag{10}$$
$$\begin{cases} \coshθ=\frac{e^{θ}+e^{-θ}}{2}\\
\sinhθ=\frac{e^{θ}-e^{-θ}}{2} \end{cases} \tag{11}$$
である。これらの式から $θ$ について解けば、それぞれの逆関数を求めることができる。ここでは例として $x=\sinθ$ の逆関数を求めるが、読者には他の関数も導出してみてほしい。
$$x=\sinθ=\frac{e^{iθ}-e^{-iθ}}{2i}$$
$$∴ \left(e^{iθ}\right)^2 -2ix\left(e^{iθ}\right)-1=0$$
$$\begin{align*}
∴ e^{iθ} &=ix±\sqrt{1-x^2}\\
∴ iθ&=\log(ix±\sqrt{1-x^2})\\
∴ θ&=-i\log(ix±\sqrt{1-x^2})
\end{align*} \tag{16}$$
となる(複号同順)。そこで得られた(15)式と、(8)式
$$e^{iθ} =i\sinθ+\cosθ \tag{8}$$
の両辺を対数 $\log$ の肩に乗せ導かれる $θ$
$$\begin{align*}
e^{iθ} &=i\sinθ+\cosθ\\
∴ θ&=-i\log(i\sinθ+\cosθ)
\end{align*} \tag{17}$$
を比較する。ここで $x=\sinθ$ であることから、途中の $\log$ の中の $±$ は $\sinθ$ における $θ$ の変域に対する $\cosθ$ の正負の取り方に由来することが分かる。
一般的に $\sinθ$ の定義域は $-\frac{π}{2} ≤θ≤\frac{π}{2}$ であるが、このとき $\cosθ$ は正の値を取り得る。よって一般的に求める関数 $\arcsin x$ は
$$∴ \arcsin x=θ_{(x)}=-i\log(ix+\sqrt{1-x^2}) \tag{18}$$
となる。これと $\arccos x+\arcsin x=\frac{π}{2}$ から $\arccos x$ は
$$\begin{align*}\arccos x=\frac{π}{2} -\arcsin x&=\frac{π}{2} +i\log(ix+\sqrt{1-x^2}) \\
&=i\left\{-i\frac{π}{2} +\log(ix+\sqrt{1-x^2})\right\}\\
&=i\log(-i(ix+\sqrt{1-x^2}))
\\∴ \arccos x&=-i\log(i(-ix+\sqrt{1-x^2}))\\
&=-i\log(x+i\sqrt{1-x^2}))
\end{align*} \tag{19}$$
となる(なぜか知らないがWikiでの $\text{arccos}\hspace{1mm}x$ の対数表示では $i\sqrt{1-x^2}$ の符号がマイナスになっているが見なかったことにしよう……)。勿論指数関数表示から求めても良い。同様に計算すれば双曲線関数の方も
$$\text{arsinh}\hspace{1mm} x=\log(x+\sqrt{1+x^2}) \tag{20}$$
$$\text{arcosh}\hspace{1mm} x=\log(x+\sqrt{x^2-1}) \tag{21}$$
のように求められる。ただし(20)式の $\sqrt{x^2-1}$ の部分は、考える双曲線関数が実数内での想定であるものとし、複素数を含めた一般の場合には $\sqrt{z+1}\sqrt{z-1}$ となる。このことは $\cosh x$ が実数全域で全射ではないことに由来する。 $\tan x$ と $\tanh x$ の導出の仕方は少し特殊で、例えば
$$x=\tanθ=\frac{\sinθ}{\cosθ} =\frac{e^{iθ}-e^{-iθ}}{i(e^{iθ}+e^{-iθ})}$$
を変形して求めても良いが、
$$x^2=\tan^2θ=1-\frac{1}{\cos^2θ}$$
から $\cos^2θ$ を求め、これから $\sin^2θ,\cosθ\sinθ$ を $x$ で表現する。これらを
$$e^{2iθ}=(\cosθ+i\sinθ)^2=\cos^2θ-\sin^2θ+2i\sinθ\cosθ$$
に代入して $θ$ について解くことでも求められる。
例
実際に以下のような質問を受けたことがある。
「方程式 $2^x+2^{-x}=4$ の解法で $2^x$ について解くものしかないが、 $2^{-x}$ について解いても結果が変わらないのはなぜか」
解法は幾つかあるが、高校数学の参考書に載っているのは
- $2^x$ を両辺に掛けて $2^x$ についての2次方程式と見なす
- 解と係数の関係から2解を $2^x,2^{-x}$ とする2次方程式 $t^2-4t+1=0$ を解く
の2つである。どちらも $2^x$ についての方程式と見なしているが、別に $2^{-x}$ についての方程式と見なして解いても結果は変わらないのだ。
そこで先述までに解説した双曲線関数、逆双曲線関数を利用してみる。
さて与えられた方程式
$$2^x+2^{-x}=4 \tag{22}$$
の左辺について $2^x=e^t$ (このとき $t=x\log 2$ )と置くと、
$$\begin{align*}
e^t+e^{-t}&=4\\
\frac{e^t+e^{-t}}{2}&=2\\
∴ \cosh t&=2 (∵(11)式)\\
∴ t&=±\text{arcosh}\hspace{1mm} 2
\end{align*}$$
となる。右図の通り $y=\cosh x$ を $y=x$ を軸に折り曲げたものは $y=±\text{arcosh}\hspace{1mm} x$ となる。
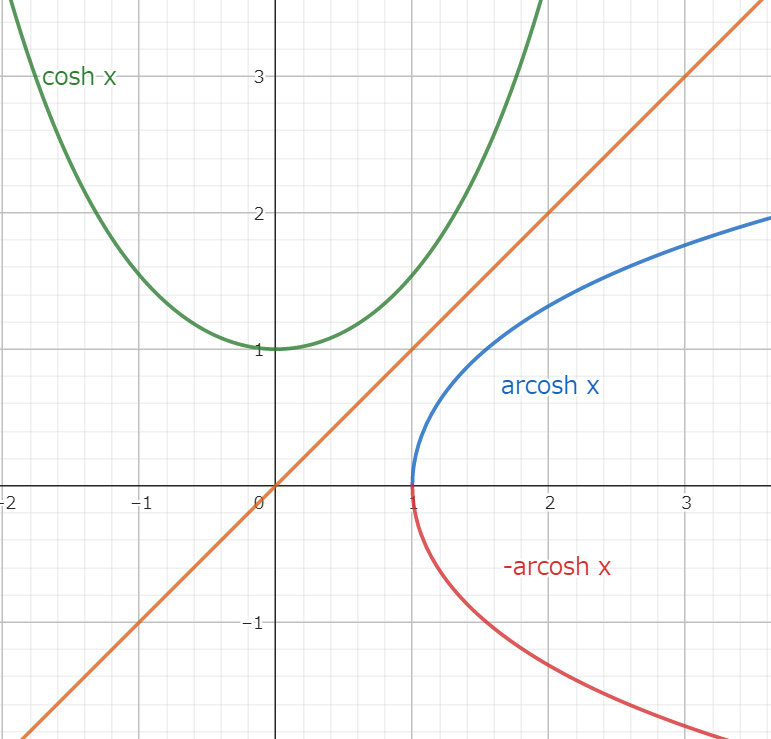
$t=x\log 2$ であるから
$$∴ x=±\frac{\text{arcosh}\hspace{1mm} 2}{\log 2} \tag{23}$$
ここで逆双曲線関数
$$\text{arcosh}\hspace{1mm} x=\log(x+\sqrt{x^2-1}) \tag{21}$$
の $x=2$ に代入することで
$$\text{arcosh}\hspace{1mm} 2=\log(2+\sqrt{3}) \tag{24}$$
であることから(23)式は
$$x=±\frac{\log(2+\sqrt{3})}{\log 2} =±\frac{\log\left\{(2+\sqrt{3})^{±1}\right\}}{\log 2} =\frac{\log(2±\sqrt{3})}{\log 2} \tag{25}$$
となる。よって $-x$ について解いたのなら
$$-x=∓\frac{\log(2+\sqrt{3})}{\log 2} =\frac{\log\left\{(2+\sqrt{3})^{∓1}\right\}}{\log 2} =\frac{\log(2∓\sqrt{3})}{\log 2} \tag{26}$$
となり、結局(25),(26)式は同じことである。
逆三角関数と逆双曲線関数の導関数
関数 $y=f(x)$ の逆関数 $y=f^{-1}(x)$ の導関数と言えば、 $x=f(y)$ の導関数
$$\frac{dx}{dy}=f'(y)$$
の逆数が
$$\frac{1}{\frac{dx}{dy}}=\frac{dy}{dx}=\frac{1}{f'(y)}$$
であるかのように計算することで求められる。
では具体的に $y=f(x)=\sin x (-\frac{π}{2}≤x≤\frac{π}{2})$ の逆関数 $y=\arcsin x (-1≤x≤1)$ の導関数を求める。
$$\frac{dx}{dy}=f'(y)=\cos y$$
$$∴ \frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-x^2}}$$
となる。最後の $\cos y=±\sqrt{1-x^2}$ の変換で $±$ のうち $+$ を選択したのは $-\frac{π}{2}≤y≤\frac{π}{2}$ の範囲で $\cos y$は $0≤x≤1$ となるからである。
以下同様に計算することで
$$\begin{cases} \frac{d}{dx} \arcsin x=\frac{1}{\sqrt{1-x^2}}\\
\frac{d}{dx} \arccos x=-\frac{1}{\sqrt{1-x^2}}\\
\frac{d}{dx} \arctan x=\frac{1}{1+x^2}\\
\end{cases} \tag{27}$$
$$\begin{cases} \frac{d}{dx} \text{arsinh}\hspace{1mm} x=\frac{1}{\sqrt{1+x^2}}\\
\frac{d}{dx} \text{arcosh}\hspace{1mm} x=-\frac{1}{\sqrt{x^2-1}}\\
\frac{d}{dx} \text{artanh}\hspace{1mm} x=\frac{1}{x^2-1}\\
\end{cases} \tag{28}$$
が得られる。勿論複素対数表示したものを微分しても求まる。
例
積分
$$∫_0^1 \frac{dx}{\sqrt{1+x^2}} \tag{29}$$
を求めるというもの。よくあるのは $x=\tanθ$ と置いてから $t=\sinθ$ と置いて $\log$ の定積分とするというものだが、これでは計算が煩雑になりやすい上に $\tanθ$ で置くのか、他の三角関数で置くのか考えなければならない。
しかし(28)式より被積分関数が双曲線関数 $\text{Arsinh}\hspace{1mm} x$ の不定積分となっていることに気付けば、
$$(28)=\left[\text{Arsinh}\hspace{1mm} x\right]_0^1=\log(1+\sqrt{2})$$
と一瞬で求まる。勿論双曲線関数を使いたくないのなら $x=it$ と置くことで、
$$(28)=∫_0^{-i} \frac{idt}{\sqrt{1-t^2}}=\left[i\arcsin x\right]_0^{-i}=\log(1+\sqrt{2})$$
のように逆三角関数を利用して求めることができ、これは逆双曲線関数の場合と一致する。それもそのはずで、(18),(20)式から逆三角関数 $\arcsin$ と逆双曲線関数 $\text{arsin}\hspace{1mm}$ は
$$i\arcsin x=\text{arsinh}\hspace{1mm} (ix)$$
を満たすことが分かる。なんとも不思議な関係式である。これと前回の記事の(12)式
を見比べてみると面白いかもしれない。
終わりに
本記事では逆三角関数と逆双曲線関数について解説してみた。本記事と前回の記事とを合わせて、三角関数と双曲線関数、複素指数関数と複素対数関数の性質が少しでも伝わってくれたと思う。これらを使って、今までなんとなく解いてきた積分や計算についてその背景を知ることができたのなら幸いである。



コメント