初めに
本記事では直交座標系、直交系、非直交系(斜交座標系)という3つの観点から幾何ベクトル空間(ユークリッド空間)とその表現について考察します。それぞれの観点で直線や三角形を例に取り上げ、ベクトルの性質や関係性を説明します。またそれぞれの座標系がどのように幾何ベクトル空間を表現するか、そしてそれらがどのように関連しているかについても触れます。
まず正規直交系では、直線とその法線ベクトル、および直線上の任意の点を表現するベクトルについて再確認します。正規直交系は最も単純化され、また私達に最も馴染みのある空間と言えます。ここでの観念や常識が他の座標系においてどのように表現されるのか見ていくことになります。
次に直交系では、異なるスケールの座標軸を持つ直線とその三角形について考えます。正規直交系では規格化されていた基底について考えますが、ここではその大きさを変えた場合にどのような振る舞いを見せるのか見ていこうと思います。
最後に非直交系では、直交しない二つのベクトルが形成する三角形とその座標変換について考えます。ここではベクトルを基底の線型結合で表現せず、単位ベクトルの線型結合によって表現します。この空間は他の空間と比較して一般化されていて、斜交座標系の考え方を取り入れることで線型代数学やベクトル解析学では絶大な効果を発揮することになりましょう。
正規直交系
馴染みのある座標系
中学・高校では何気なく座標空間を使用してきた。中学・高校では座標空間と言えば特に断りが無い場合には正規直交系の幾何ベクトル空間のことを指している。正規直交系とはベクトルを単位ベクトルの線型結合で表現したときに、単位ベクトルが規格化条件と直交条件を同時に満足する内積空間のことを言う。正規直交系の代表例としてデカルト座標系や極座標系が挙げられる。本章ではデカルト座標系における直線を用いて正規直交系における幾何ベクトル空間を考える。
正規直交系を成すデカルト座標系の直線
直線
$$x+y=1 \tag{1}$$
は2次元のデカルト座標系において $\boldsymbol{n}_{(x,y)}=(1,1)$ を法線ベクトル $\boldsymbol{n}$ の1つとする。またこの直線(1)と $x$ 軸と $y$ 軸の交点を結ぶ図形 $OAB$ は $OA=OB=1$ とする直角二等辺三角形である。この直角二等辺三角形 $OAB$ を考えていこう。
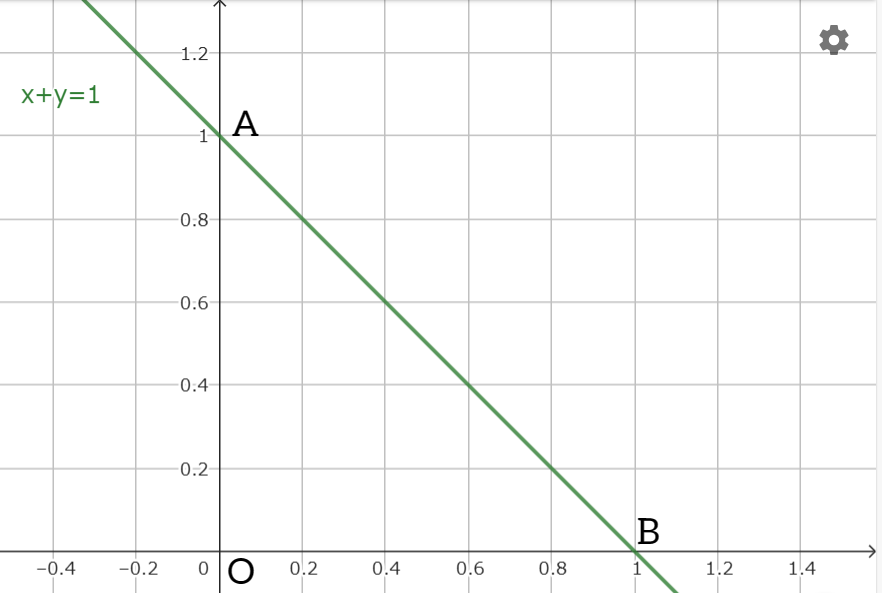
直線(1)で囲まれた直角二等辺三角形 $OAB$ は2つのベクトル $\overrightarrow{OA},\overrightarrow{OB}$ を用いて
$$\begin{cases}
|\overrightarrow{OA}|=|\overrightarrow{OB}|=1\\
\overrightarrow{OA}\cdot \overrightarrow{OB}=0
\end{cases} \tag{2}$$
という条件によって書き表される。この条件(2)は $△OAB$ について規格化条件(上式)かつ直交条件(下式)を併せている。このことから条件(2)は $△OAB$ についての規格化直交条件と言える。
ここで直線(1)を満たす $(x,y)$ をベクトル空間 $V$ におけるベクトル $\overrightarrow{OP}=\boldsymbol{r}$ とし、これを2つの単位ベクトル $\langle\boldsymbol{e}_1,\boldsymbol{e}_2\rangle$ によって、
$$\boldsymbol{r}=x\boldsymbol{e}_1+y\boldsymbol{e}_2$$
と表現することにする。
ここで直線(1)において2つのベクトル $\overrightarrow{OA},\overrightarrow{OB}$ とは正しくベクトル空間 $V$ において単位ベクトル $\langle\boldsymbol{e}_1,\boldsymbol{e}_2\rangle$ を表し、規格化直交条件
$$\boldsymbol{e}_m\cdot\boldsymbol{e}_n=δ_{mn}$$
よりこの単位ベクトルは正規直交系を成す。
よって直線(1)における法線ベクトル $\boldsymbol{n}=\boldsymbol{e}_1+\boldsymbol{e}_2$ と、直線(1)の方向ベクトル $\overrightarrow{AP}=x\boldsymbol{e}_1+(y-1)\boldsymbol{e}_2$ について内積を取ると、
$$\begin{align*}
\boldsymbol{n}\cdot \overrightarrow{AP}
&=x(\boldsymbol{e}_1\cdot\boldsymbol{e}_1)+(x+y-1)(\boldsymbol{e}_1\cdot\boldsymbol{e}_2)+(y-1)(\boldsymbol{e}_2\cdot\boldsymbol{e}_2)\\
&=x+y-1
\end{align*}$$
となり、これが $0$ となることから直線(1) $x+y=1$ を得る。
ここで基底 $\langle\boldsymbol{e}_1,\boldsymbol{e}_2\rangle$ によって成すベクトル空間 $V$ における任意のベクトル $\overrightarrow{OP}=\boldsymbol{r}$ は、直線(1)に平行な直線によって表現することが可能である。従って直線(1)に平行な直線 $x+y=c$ によってベクトル空間 $V$ が表現されるのなら、ベクトル空間 $V$ は完全正規直交系となる。
直交系
斜交座標系に向けたただの導入
正規直交系ではベクトルを規格化された基底による線型結合で表現した。最終的には非直交系(斜交座標系)によるベクトルを表現しようと考えている。そのために本章ではベクトルを正規化していない基底による線型結合で表現したときの幾何ベクトル空間を見ていこう。規格化されていない座標系はあまり勝手が良くはないが。
規格化されていない直交系
デカルト座標系において直線
$$ax+by=1 \tag{3}$$
と $x$ 軸、 $y$ 軸で囲まれた $△OAB$ について考える。つまりこの三角形における2辺 $OA,OB$ の比が基底の大きさの比となるような幾何ベクトル空間で考えようというものである。
直線(1)で囲まれた直角二等辺三角形 $OAB$ は2つのベクトル $\overrightarrow{OA},\overrightarrow{OB}$ を用いて
$$\begin{cases}
|\overrightarrow{OA}|=\dfrac{1}{a}\\
|\overrightarrow{OB}|=\dfrac{1}{b}\\
\overrightarrow{OA}\cdot \overrightarrow{OB}=0
\end{cases} \tag{4}$$
という条件によって書き表される。これは(1)の正規直交系のときとは違い、直交条件のみを満足する。
よってこのとき $△OAB$ を成す基底 $\langle\boldsymbol{e}_1,\boldsymbol{e}_2\rangle$ は
$$\begin{cases}
\boldsymbol{e}’_1\cdot\boldsymbol{e}’_1=\dfrac{1}{a^2}\\
\boldsymbol{e}’_2\cdot\boldsymbol{e}’_2=\dfrac{1}{b^2}\\
\boldsymbol{e}’_1\cdot\boldsymbol{e}’_2=0
\end{cases}
$$
を満たす。よってベクトル空間 $V’$ におけるベクトル $\boldsymbol{r}$ を
$$\boldsymbol{r}=x’\boldsymbol{e}’_1+y’\boldsymbol{e}’_2$$
と置くと、ベクトル空間 $V’→V$ の変換で
$$\begin{align*}
\boldsymbol{r}&=\dfrac{x’}{a}\boldsymbol{e}_1+\dfrac{y’}{b}\boldsymbol{e}_2\\
&=\dfrac{bx’\boldsymbol{e}_1+ay’\boldsymbol{e}_2}{ab}
\end{align*}$$
のように置換される。このため直線(3)で表現される座標系は直線(2)で表現される座標系を $b:a$ に分けている(ただし図形的には解釈していない)と言えよう。
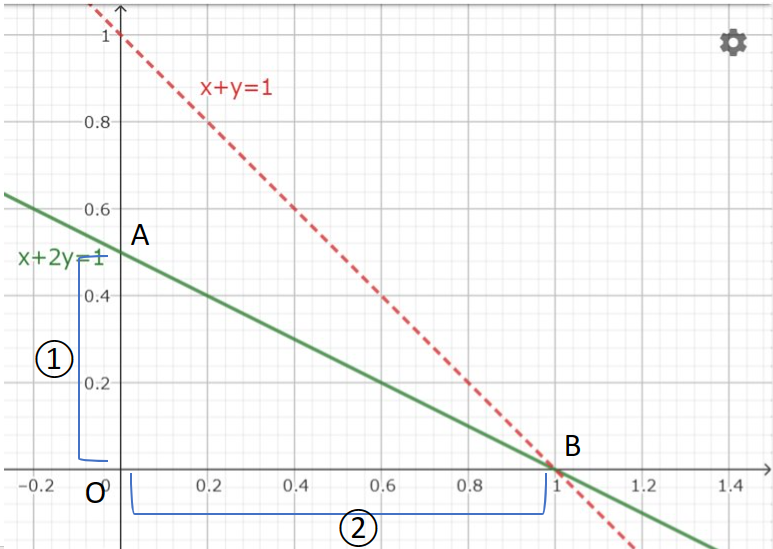
$OA:OB=1:2$ を満たす
非直交系(斜交座標系)
好きな直線に囲まれた座標系
直交系における幾何ベクトル空間はデカルト座標系にける $x$ 軸と $y$ 軸に囲まれた直角三角形の2辺を基底とした。しかし一般には直線によって囲まれ、更には直角三角形とは限らない。そこで本章では非直角三角形で表現されるような幾何ベクトル空間を考えていく。この考え方は線型代数学やベクトル解析学で役に立つ。
直線に囲まれた幾何ベクトル
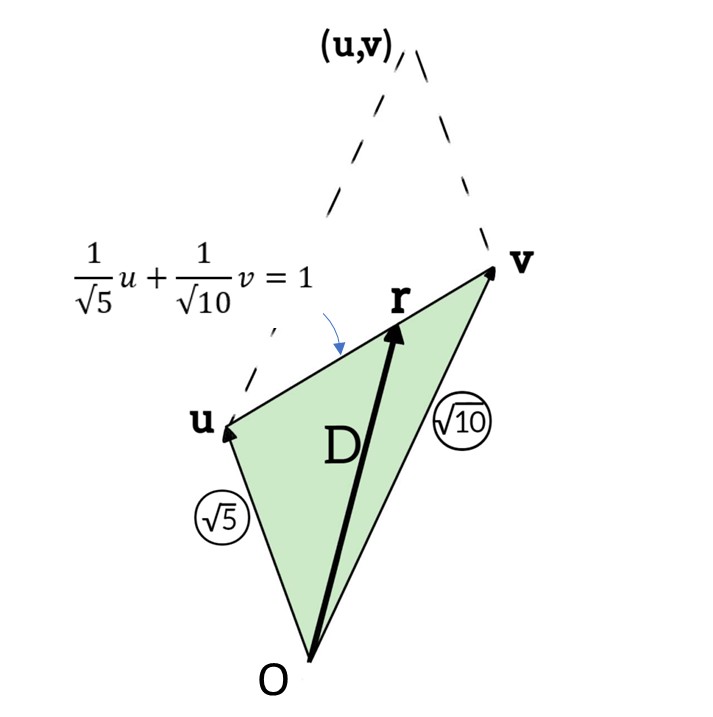
では $△OAB$ が直角三角形ではない場合を見ていこう。この場合は $△OAB$ を成す2つのベクトル $\overrightarrow{OA},\overrightarrow{OB}$ が直交していないということである。つまりこれらの単位ベクトル $\boldsymbol{e}_u,\boldsymbol{e}_v$ は
$$\boldsymbol{e}_u\cdot\boldsymbol{e}_v≠0$$
のように線型従属である場合について考えていく。
より具体的にこれらの単位ベクトルの成す角を $θ$ と置くことにする。このときベクトル空間 $V'{}’$ におけるベクトル $\boldsymbol{r}$ を
$$\boldsymbol{r}=u\boldsymbol{e}_u+v\boldsymbol{e}_v$$
と置く。これは斜交座標系 $(u,v)$ における点となる。
ここで直線 $AB$ が
$$au+bv=1\tag{5}$$
と表される場合には、単位ベクトル $\boldsymbol{e}_u,\boldsymbol{e}_v$ は
$$\begin{cases}
\boldsymbol{e}_u\cdot\boldsymbol{e}_u=\dfrac{1}{a^2}\\
\boldsymbol{e}_v\cdot\boldsymbol{e}_v=\dfrac{1}{b^2}\\
\boldsymbol{e}_u\cdot\boldsymbol{e}_v=\cosθ
\end{cases}\tag{6}$$
を満たす。
$$\begin{align*}
\boldsymbol{r}\cdot\boldsymbol{e}_1&=(u\boldsymbol{e}_u+v\boldsymbol{e}_v)\cdot\boldsymbol{e}_1\\
∴ x\boldsymbol{e}_1&=u\boldsymbol{e}_u\cdot\boldsymbol{e}_1+v\boldsymbol{e}_v\cdot\boldsymbol{e}_1\\
y\boldsymbol{e}_2&=\boldsymbol{r}-x\boldsymbol{e}_1\\
\end{align*}$$
により、変数 $(x,y)→(u,v)$ への置換が可能となる(今回は2次元であるが、3次元以上の場合にも拡張が可能)。
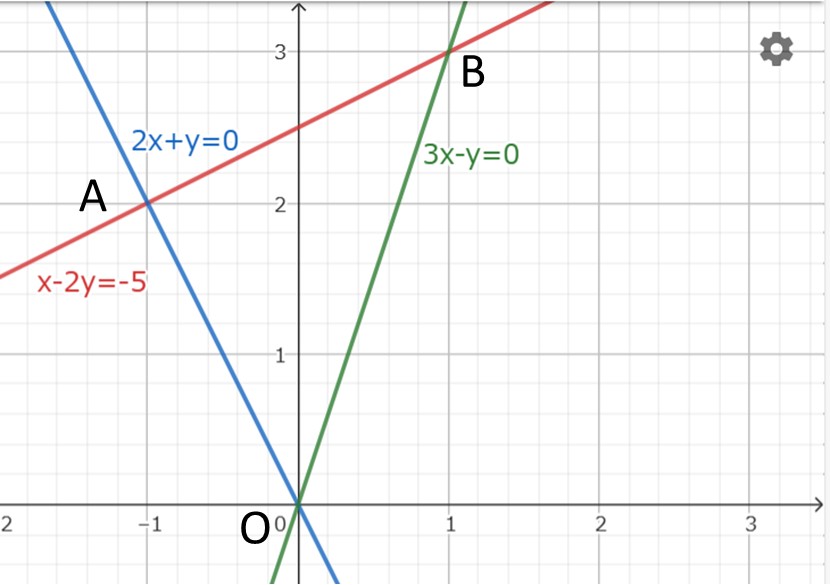
デカルト座標系において
$\overrightarrow{OA}=(-1,2),\overrightarrow{OB}=(1,3)$
となる
最後に
本記事では幾何ベクトル空間について、非直交系(斜交座標系)について考えてみた。本記事のように勝手に何かしらのベクトルの線型結合で表現することで簡単に問題を処理することができることがある。
使用例


コメント