射影演算子の図形的な解釈

本記事は4部構成のシリーズ「線型演算子 $\hat{A}$ を解析してみた」の第2部となります。第2部では線型演算子の解析に必要な射影演算子を紹介していきます。

前書き

本記事では射影演算子という線型代数の概念について詳しく説明しています。射影演算子は正方行列であって、自分自身の二乗が自分自身と等しいものを指します。この性質は、射影演算子があるベクトル空間をその部分空間へ「射影」するという直感的な解釈につながります。

また射影演算子の積が $\hat{O}$ となる性質から、ベクトル空間の直和分解に密接に関連しています。つまりあるベクトル空間が二つの部分空間の直和として表されるとき、射影演算子は元のベクトル空間の元を部分空間へ一意的に写す変換となります。

射影演算子 $\hat{P}$

前章で射影演算子という名前が出てきた。ここでは射影演算子について少し詳しく見ていこうと思う。

射影演算子の定義は以下のようになる

正方行列 $\hat{P}$ について

$$\hat{P}^2=\hat{P}\tag{12}$$

を満たすものを射影演算子と言う。

射影演算子

(12)式を変形すると、射影演算子 $\hat{P}$ についての多項式

$$\begin{align*}
\hat{P}^2-\hat{P}&=0\\
∴\hat{P}(\hat{P}-\hat{I})&=0\\
∴\hat{P}(\hat{I}-\hat{P})&=0\tag{13}\\
∴X(\hat{I}-X)&=0 \tag{14}
\end{align*}$$

が得られる。(14)式は相違なる一次因子の積で表現され、かつこれが $(右辺)=0$ となっていることから、(14)式は最小多項式となる。

ここで最小多項式の定義は以下に示す。

線型演算子 $\hat{A}$ についての多項式 $q(X)$ について

$$q(X)=\hat{O}$$

が成り立つもののうち、最高字係数が $1$ であり、かつ最小次数 であるものを最小多項式と言う。

最小多項式

最小多項式について以下の主張は同値である（出典：Wiki）。

1. $λ$ は $A$ の最小多項式 $q(X)$ の根である。
2. $λ$ は $A$ の固有多項式の根である。
3. $λ$ は $A$ の固有値である。

よって射影演算子 $\hat{P}$ についての多項式(13)式から射影演算子 $\hat{P}$ の固有値 $λ$ は $λ=0,1$ となる。

ところで(13)式が意味することは、ベクトル $\boldsymbol{x}$ について合成変換 $\hat{P}(\hat{I}-\hat{P})$ によって

$$\hat{P}(\hat{I}-\hat{P})\boldsymbol{x}=\boldsymbol{0}$$

のように常に零ベクトル $\boldsymbol{0}$ へ変換されるということである。

行列の積が零行列になるということは

ベクトル $\boldsymbol{x}$ が合成変換により零行列 $0$ へ変換されるときに、デカルト座標系においてはどのように作用されるのだろうか。ここでは演算子をより限定した行列について考えていく。

ベクトル $\boldsymbol{x}$ の線型変換 $f,g$ がそれぞれ行列 $A,B$ によって表現されているとすると、この合成変換は $f◦g(\boldsymbol{x})=f(g(\boldsymbol{x}))=AB\boldsymbol{x}$ のように行列の積で表現される。

ここでいずれも非零である行列の積 $AB$ が $0$ となる場合について考えていく。つまり合成変換によりベクトル $\boldsymbol{x}$ を常に原点に返す場合の各行列を見ていこうというものである。

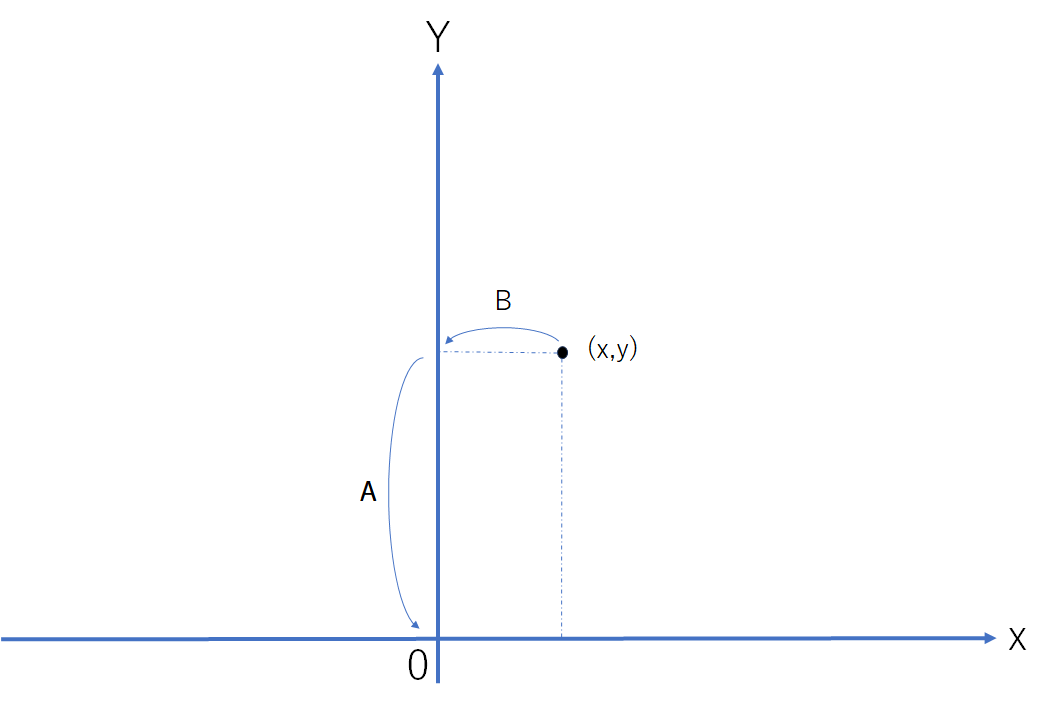
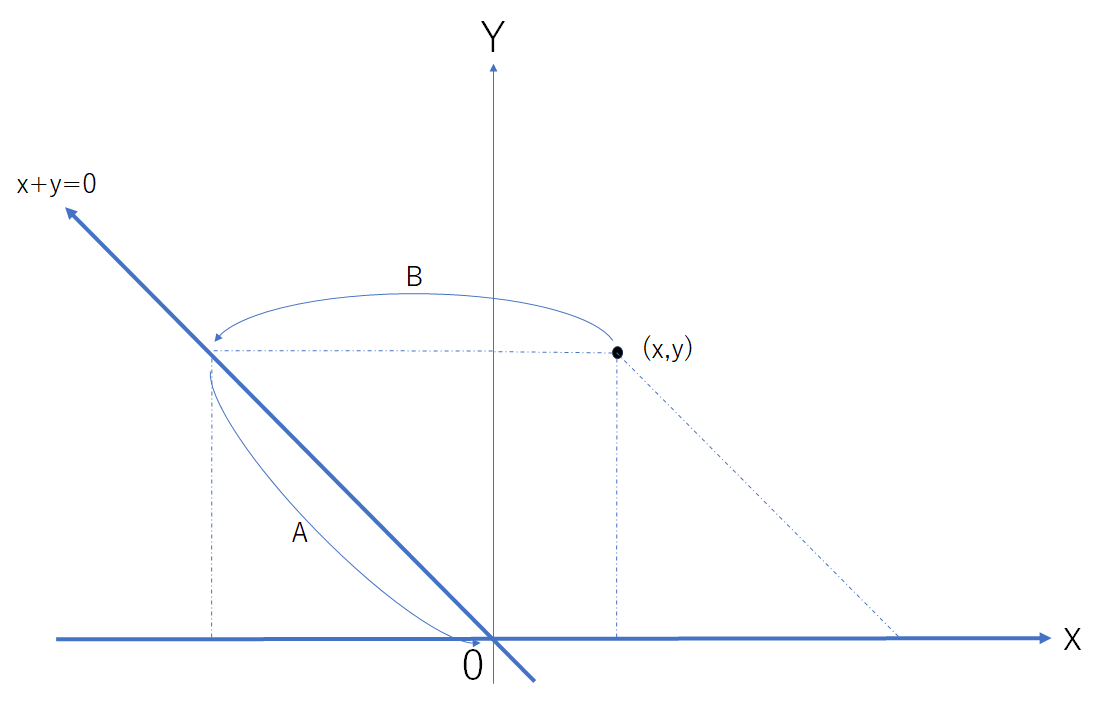
先述の2例は線型変換 $f◦g$ が、ベクトル空間 $W$ におけるベクトル $\boldsymbol{x}$ を部分ベクトル空間 $U$ の元 $\boldsymbol{u}$ と部分ベクトル空間 $V$ の元 $\boldsymbol{v}$ によって、一意的に $\boldsymbol{x}=\boldsymbol{u}+\boldsymbol{v}$ と表されていることが分かる。1番目の例では2次元デカルト座標系において $x,y$ 成分に分解していて、2番目の例では直線 $x+y=0$ 上の単位ベクトルと $x$ 軸正の向きの単位ベクトルによる斜交座標系によって分解している。

一般に非零行列である2つの行列 $A,B$ が $AB=0$ であるときには、2つの行列 $A,B$ が互いに干渉せず、このことから2つの行列 $A,B$ は直交していると言う。

射影演算子による線型変換

非零行列である行列 $A,B$ の積が $AB=0$ であることは、射影演算子の「射影」という性質を説明しているのだ。このことは射影演算子が(13)式

$$\hat{P}(\hat{I}-\hat{P})=0 \tag{13}$$

という条件を満足することからも窺える。この条件は正に2つの演算子 $\hat{P},(\hat{I}-\hat{P})$ が直交することを意味する。よってこれらの演算子によってベクトル $\boldsymbol{x}$ は部分ベクトル空間 $U,V$ の元をそれぞれ $\boldsymbol{u},\boldsymbol{v}$ として、一意的に

$$\begin{align*}
\boldsymbol{x}&=\boldsymbol{u}+\boldsymbol{v}\\ ∴\boldsymbol{x}&=\hat{P}\boldsymbol{x}+(\hat{I}-\hat{P})\boldsymbol{x}\\
\end{align*}$$

が成り立つのである。

つまり射影演算子とは元となるベクトル空間 $W$ を部分ベクトル空間 $U,V$ で直和分解 $W=U\oplus V$ としたときに、 $W$ の元 $\boldsymbol{x}=\boldsymbol{u}+\boldsymbol{v}(\boldsymbol{u}∈U,\boldsymbol{v}∈V)$ を $\boldsymbol{u}$ に写すような変換と言える。

上式ではベクトル $\boldsymbol{x}$ から $\boldsymbol{u}=P\boldsymbol{x}$ に写していることから、部分ベクトル空間 $U$ が射影演算子 $\hat{P}$ の値域となり、部分ベクトル空間 $V$ が零空間（核）と見なせる。それと同時に $(\hat{I}-\hat{P})^2=(\hat{I}-\hat{P})$ となるように、射影の値域と核は互いに相補的なものであるから、射影演算子 $(\hat{I}-\hat{P})$ にとっては部分ベクトル空間 $V$ が値域となり、このとき部分ベクトル空間 $U$ は核となることも分かる。

またベクトル $\boldsymbol{x}$ について値域 $U$ と核 $V$ が互いに直交する部分ベクトル空間となる場合には、エルミート積が $0$ になれば良く

$$\begin{align*}
\langle \hat{P}x|(\hat{I}-\hat{P})x\rangle\\
&=(\hat{P}\boldsymbol{x})^*(\hat{I}-\hat{P})\boldsymbol{x}\\
&=\boldsymbol{x}^*\hat{P}^*((\hat{I}-\hat{P}))\boldsymbol{x}
=\boldsymbol{x}^*(\hat{P}^*-\hat{P}^*\hat{P}))\boldsymbol{x}\\
&=\boldsymbol{x}^*(\hat{P}-\hat{P}\hat{P}^*)^*\boldsymbol{x}\\
&=0
\end{align*}$$

を満たす。このとき
$$\begin{align*} &\hat{P}-\hat{P}\hat{P}^*=0\\
∴&\begin{cases}
\hat{P}=\hat{P}^*\\
\hat{P}=\hat{P}^2
\end{cases}
\end{align*}$$

となる。

このように自己随伴性を満たす射影演算子は直交射影演算子（正射影演算子）と呼ばれ、ベクトル $\boldsymbol{x}$ は直交系を成す基底方向に射影される。