面は3次元ユークリッド空間(デカルト座標系なら $(x,y,z)$ )において、2つの変数 $u,v$ で表現されます。このため面で積分する面積分とは、2つの変数 $u,v$ による座標系 $(u,v)$ と、それに垂直な成分によって表現されます。しかし多くのサイトでは3変数 $(x,y,z)$ で表現される面 $S$ の面素 $dS$ を2変数 $(x,y)$ で表すというものです。計算する上ではそちらを使うのが一番手っ取り早いのですが、初学者がいきなりそのような解法しか知らされなくてどうやって理解しえましょうか。ここでは面 $S$ 上の点 $\boldsymbol{r}$ を斜交座標系 $(u,v)$ を用いることで直感的に理解しやすいものにしました。
面積分については
を確認してください。
領域 $D$ を成すベクトルによる面積分
例題
問題
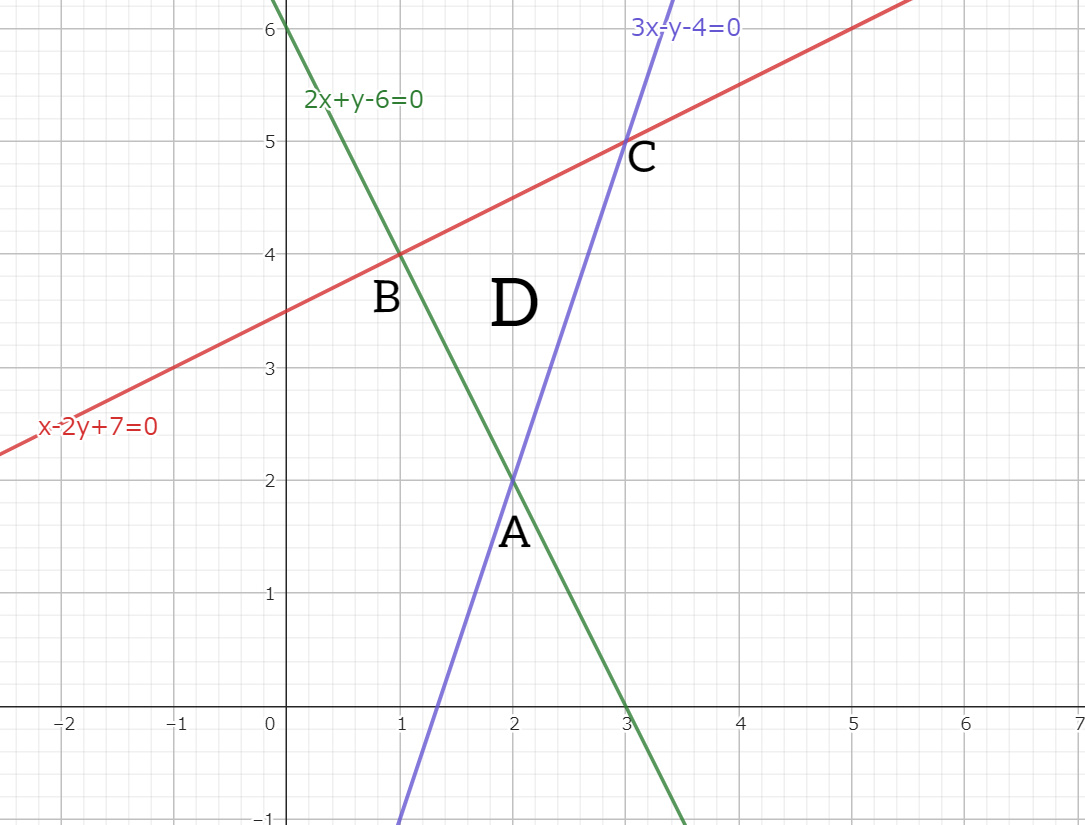
3つの直線囲まれた三角形と領域 $D$ 2次元ユークリッド空間( $xy$ 平面) において3つの直線
$$\begin{cases}2x+y-6=0\\
x-2y+7=0\\
3x-y-4=0\end{cases}$$
の交点 $A,B,C$ に囲まれる三角形 $ABC$ の領域を $D$ と置き、この領域における面積を $S$ と置く。ただし交点 $A,B,C$ は各自定めよ。このとき領域 $D$ におけるベクトル $\boldsymbol{A}_{\boldsymbol{r}}=\boldsymbol{A}_{(x,y)}$ の面積分 $\displaystyle\int_S\boldsymbol{A}_{\boldsymbol{r}}\cdot d\boldsymbol{S}$ を求めたい。そこで以下の問いに答えよ。(1)三角形の面積 $S$ を求めよ。
(2)領域 $D$ における任意のベクトル $\boldsymbol{r}$ はベクトル $\overrightarrow{AB},\overrightarrow{AC}$ の単位ベクトル $\boldsymbol{e}_b,\boldsymbol{e}_c$ を用いて
$$\boldsymbol{r}=u\boldsymbol{e}_b+v\boldsymbol{e}_c$$
と表される。そこで単位ベクトル $\boldsymbol{e}_b,\boldsymbol{e}_c$ を定義し、任意のベクトル $\boldsymbol{r}$ を $u,v$ を用いて書き表せ。更にそのときの2つの変数 $u,v$ の取り得る値の範囲を求めよ。
(3)ベクトルを $\boldsymbol{A}_{(\boldsymbol{r}_{(x,y)})}=(xy,x-y,x+y)$ として面積分 $\displaystyle\int\boldsymbol{A}_{(\boldsymbol{r}_{(x,y)})} d\boldsymbol{S}=\iint_D\boldsymbol{A_{(\boldsymbol{r_{(u,v)}})}}\cdot d\boldsymbol{S}$ を求めよ。
解答・解説
先に解答・解説を載せておく。この解説が分からない読者は後続に置いた解答・解説の解説を確認するように。
まずは3つの直線の方程式の3つの連立方程式から交点を求めると、
$$(x,y)=(1,4),(2,2),(3,5)$$
となる。それぞれ
$$A(2,2),B(1,4),C(3,5)$$
と置いてこれらを三角形ABCの各頂点とし、以下 $\overrightarrow{AB}=(-1,2),\overrightarrow{AC}=(1,3)$ とする。勿論頂点A,B,Cは入れ替えることもできるので、意欲のある読者は試してもらいたい。
(1)三角形ABCの面積 $S$ は $z$ 軸方向の成分が $0$ の下で外積$\overrightarrow{AB}\times\overrightarrow{AC}$ を用いて
$$S=\frac{1}{2}\left|\overrightarrow{AB}\times\overrightarrow{AC}\right|=\frac{5}{2}$$
となる。
(2)各単位ベクトル $\boldsymbol{e}_b,\boldsymbol{e}_c$ は $\overrightarrow{AB}=(-1,2),\overrightarrow{AC}=(1,3)$ より
$$\begin{cases}
\boldsymbol{e}_b=\dfrac{1}{\sqrt{5}}(-1,2)\\
\boldsymbol{e}_c=\dfrac{1}{\sqrt{10}}(1,3)
\end{cases}$$
よって点 $\boldsymbol{r}$ は斜交座標系 $(u,v)$ において
$$\begin{cases}
\boldsymbol{e}_b=\dfrac{1}{\sqrt{5}}(-1,2)\\
\boldsymbol{e}_c=\dfrac{1}{\sqrt{10}}(1,3)
\end{cases}$$
として
$$\boldsymbol{r}=u\boldsymbol{e}_b+v\boldsymbol{e}_c$$
と表される。
ただし
$$\begin{cases}
\overrightarrow{AB}=\sqrt{5}\boldsymbol{e}_b\\
\overrightarrow{AC}=\sqrt{10}\boldsymbol{e}_c
\end{cases}$$
また2つの単位ベクトル $\boldsymbol{e}_b,\boldsymbol{e}_c$ はこれらの内積から
$$\boldsymbol{e}_b\cdot\boldsymbol{e}_c=\dfrac{1}{\sqrt{2}}$$
となるから直交していなく、またその角度を $θ$ として
$$\cosθ=\dfrac{1}{\sqrt{2}}$$
と表される。因みに $θ=\dfrac{π}{4}$ である。
ところで領域 $D$ については $u,v≥0,u≤\sqrt{5},\dfrac{\sqrt{10}u+\sqrt{5}v}{5\sqrt{2}}≤1$ を満たすことから
領域 $D$ は $D:\{0≤u≤\sqrt{5},0≤v≤\sqrt{10}-\sqrt{2}u\}$ となる。
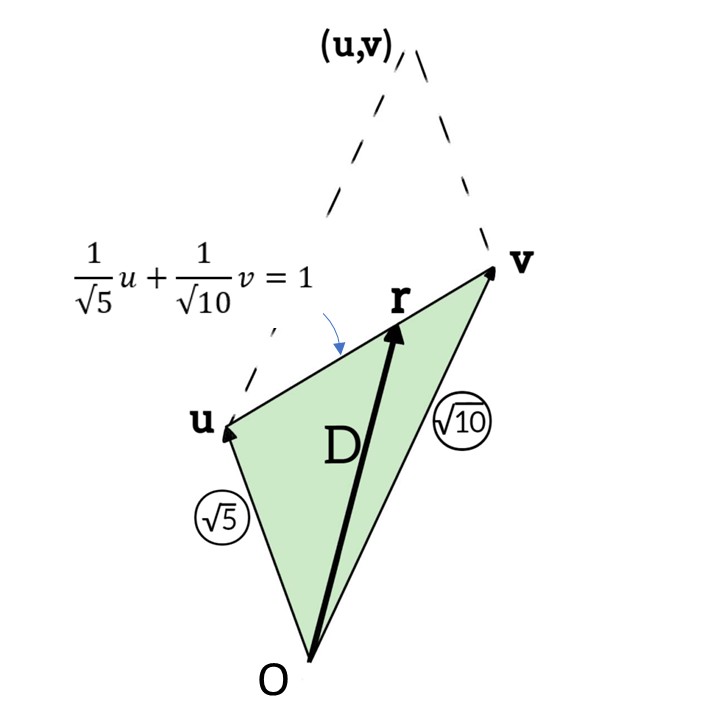
点 $A$ を始点とし、辺 $BC$ 上の点を終点とするベクトル $\boldsymbol{r}$ を斜交座標系 $(u,v)$ で表現
さて斜交座標系 $(u,v)$ における任意の点 $\boldsymbol{r}$ は
$$\boldsymbol{r}=u\boldsymbol{e}_b+v\boldsymbol{e}_c$$
と表現されるのであった。そこで基底をデカルト座標系の基底 $\langle\boldsymbol{e}_x,\boldsymbol{e}_y\rangle$ に変換する。このときデカルト座標系は正規直交基底であるから以下のように変換される。
$$\begin{align*}
\boldsymbol{r}\cdot\boldsymbol{e}_x&=u\boldsymbol{e}_b\cdot\boldsymbol{e}_x+v\boldsymbol{e}_c\cdot\boldsymbol{e}_x\\
∴ x\boldsymbol{e}_x&=\left(\dfrac{-1}{\sqrt{5}}u+\dfrac{1}{\sqrt{10}}v\right)\boldsymbol{e}_x\\
∴ y\boldsymbol{e}_y&=\boldsymbol{r}-x\boldsymbol{e}_x\\
&=\left(\dfrac{2}{\sqrt{5}}u+\dfrac{3}{\sqrt{10}}v\right)\boldsymbol{e}_y
\end{align*}$$
よって
$$\boldsymbol{r}=
\begin{pmatrix}
x\\
y
\end{pmatrix}
=\begin{pmatrix}
\dfrac{-1}{\sqrt{5}}u+\dfrac{1}{\sqrt{10}}v\\
\dfrac{2}{\sqrt{5}}u+\dfrac{3}{\sqrt{10}}v
\end{pmatrix}
$$
(3)ヤコビ行列式 $|\boldsymbol{J}|$ により面素 $d\boldsymbol{S}$ は
$$\begin{align*}
d\boldsymbol{S}&=\left(\dfrac{∂\boldsymbol{r}}{∂u}\times\dfrac{∂\boldsymbol{r}}{∂v}\right)dudv
\\&=|\boldsymbol{J}|\boldsymbol{e}_zdudv\\
&=\dfrac{1}{\sqrt{2}}\boldsymbol{e}_zdudv
\end{align*}$$
となる。
また題意のベクトル $\boldsymbol{A_{(\boldsymbol{r})}}=(xy,x-y,x+y)$ は変数 $u,v$ を用いて
$$\boldsymbol{A_{(\boldsymbol{r})}}=
\begin{pmatrix}
-\dfrac{2}{5}u^2+\dfrac{3}{10}v^2-\dfrac{1}{5\sqrt{2}}uv\\
-\dfrac{3}{\sqrt{5}}u-\dfrac{2}{\sqrt{10}}v\\
\dfrac{1}{\sqrt{5}}u+\dfrac{4}{\sqrt{10}}v
\end{pmatrix}$$
と書き替えられる。といっても面素が $\boldsymbol{e}_z$ を向いているので、 $z$ 方向の成分しか必要ない。よって求める面積分は
$$\begin{align*}
\int_S\boldsymbol{A_{(\boldsymbol{r})}}\cdot d\boldsymbol{S}&=\iint_D\boldsymbol{A_{(\boldsymbol{r_{(u,v)}})}}\cdot d\boldsymbol{S}\\
&=\int_0^{\sqrt{5}}du\int_0^{\sqrt{10}-\sqrt{2}u}dv\hspace{1mm}\left(\dfrac{1}{\sqrt{5}}u+\dfrac{4}{\sqrt{10}}v\right)\dfrac{1}{\sqrt{2}}\\
&=\int_0^{\sqrt{5}}du\hspace{1mm}\left(\dfrac{1}{\sqrt{5}}u\left(\sqrt{10}-\sqrt{2}u\right)+\dfrac{4}{2\sqrt{10}}\left(\sqrt{10}-\sqrt{2}u\right)^2\right)\dfrac{1}{\sqrt{2}}\\
&=\int_0^{\sqrt{5}}du\hspace{1mm}\left(\left(\dfrac{4}{\sqrt{10}}-\dfrac{\sqrt{2}}{\sqrt{5}}\right)u^2+\left(\sqrt{2}-4\sqrt{2}\right)u+2\sqrt{10}\right)\dfrac{1}{\sqrt{2}}\\
&=\left(\left(\dfrac{4}{\sqrt{10}}-\dfrac{\sqrt{2}}{\sqrt{5}}\right)\dfrac{5}{3}\sqrt{5}-3\sqrt{2}\dfrac{5}{2}+2\sqrt{10}\sqrt{5}\right)\dfrac{1}{\sqrt{2}}\\
&=\dfrac{1}{\sqrt{5}}\dfrac{5}{3}\sqrt{5}-15+10\\
&=-\dfrac{10}{3}
\end{align*}$$
解答・解説終わり
解答・解説の解説
本記事の例題では面積分を領域 $D$ 内に存在するベクトル $\boldsymbol{r}$ を2つの変数 $u,v$ に置換することで実現した。この置換は好きな2つの変数を選択することができるので、例題では2つの直線の方向ベクトルの方向を単位ベクトルの向きとして、斜交座標系 $uv$ によってベクトル $\boldsymbol{r}$ を記述した。このように好きな2つの変数を選択することで、煩雑な計算を防ぐことができるだけではなく計算の概要がよく分かるのだ。今回の例題では領域 $D$ が $xy$ 平面上の三角形の内部であったが、これが例えば $x$ 軸 $y$ 軸 $z$ 軸と平面 $x+y+z=1$ に囲まれる三角形についても同様に考えることができるし、勿論球面や傾けた円等にも適用可能である。
(1)はまあ被積分ベクトルを $\boldsymbol{1}$ と見なして面積分を実行したもの、つまり
$$\int_S\boldsymbol{1}\cdot d\boldsymbol{S}=\int_SdS=\iint_DdS$$
が領域 $D$ における三角形 $S$ の面積を表すことを確かめられるようにという想いからである。
(2)では2つの直線の方向ベクトルの方向を単位ベクトルの方向とし、面積分の変数をこの単位ベクトルの各成分 $(u,v)$ とした。つまり領域 $D$ における任意のベクトル $\boldsymbol{r}$ を斜交座標系 $(u,v)$ で扱うということである。これにより領域 $D$ における面積分を視覚的に直感的に分かりやすく捉えることができるようになったのだ。読者にもよくあるよく分からん面素の公式を闇雲に使って計算するような計算からは解放されたい。
領域 $D$ の変数 $u,v$ の取り得る値の範囲について、
$$u,v≥0,u≤\sqrt{5},\dfrac{\sqrt{10}u+\sqrt{5}v}{5\sqrt{2}}≤1$$
を満たすと書いた。
この第2式は斜交座標系 $(u,v)$ において、ベクトル $\boldsymbol{r}$ は平面 $S$ 内の直線 $x-2y+7=0$ に平行な線分を用いて任意の点 $\boldsymbol{r}=(u,v)$ を表現しているのである。ここで $\boldsymbol{r}=(u,v)$ とは直線 $u+v=1$ で形成される二等辺三角形の長さの等しい2辺を単位ベクトルに取っている。そこで $A(2,2)$ を始点として直線 $x-2y+7=0$ に平行な線分上にある点 $\boldsymbol{p}$ を終点とする題意の点 $\boldsymbol{r}$ は、 $u$ 成分と $v$ 成分の比が $\sqrt{5}:\sqrt{10}$ であると見なすことができる。つまり
$$\dfrac{\sqrt{10}u+\sqrt{5}v}{5\sqrt{2}}$$
とは斜交座標系 $(u,v)$ を $\sqrt{5}:\sqrt{10}$ に内分する点の集まり(つまり直線 $x-2y+7=0$ に平行な直線)を表現している。


よって
$$\dfrac{\sqrt{10}u+\sqrt{5}v}{5\sqrt{2}}=1$$
のときには点 $\boldsymbol{p}$ は直線 $x-2y+7=0$ 上の点に一致する。
なお点 $\boldsymbol{p}$ が存在する線分の求め方は、今までに切片が分かる直線の方程式を求めるために使われてきたものなので、忘れてしまっている読者は確認しておこう。今までは正規直交系 $(x,y)$ によって議論されてきたので、直線 $x+y=1$ で形成される三角形は直角二等辺三角形となった。しかし斜交座標系の場合には単に二等辺三角形となるのだ。
領域 $D$ における任意のベクトル $\boldsymbol{r}$ について、正規直交基底による基底の変換を行った。 $\langle\boldsymbol{e}_x,\boldsymbol{e}_y\rangle$ は正規直交基底であるから見かけ上は
$$x\boldsymbol{e}_x+y\boldsymbol{e}_y=\boldsymbol{r}$$
を $y\boldsymbol{e}_y$ についての式に変形したように見えるが、実際にはシュミットの直交化に則っていることに注意されたい。
(3)では漸く面積分を実行した。本例題では面素の向きが $xy$ 平面に垂直な向きとなることから、結局ベクトル $\boldsymbol{A}$ は $xy$ 平面に垂直な成分のみ(デカルト座標系 $(x,y)$ においては $z$ 成分)しか影響しない。考えている面 $S$ が $xy$ 平面だからあまりありがたみを感じないかもしれないが、一般に2つのベクトル $u,v$ で形成される座標系によってベクトル $\boldsymbol{A}$ を置換することで本例題のように考えることができるのだ。
斜交座標系については以下の記事で解説している。



コメント