高校数学では1変数 $x$ についての積分をしました。この積分が定積分の場合には $xy$ 平面において面を形成します。そこで形成された面によって積分を定義できなかろうか、というのが面積分なのです。しかしこの面積分はベクトル解析学を学ぶ学生が苦労するであろう三積分(体積分、線積分、面積分)の1つに該当します。そこで本記事では高校数学の積分から自然な形で面積分へ拡張していきましょう。最終的には面積分の公式のようなものを導出することになりますが、結局理解していればどうってことのない式ではあります。私は多分使わないかな……。
三積分の内線積分を解説した記事はこちら
面積分とは
定積分を変形して面積分と解釈してみる
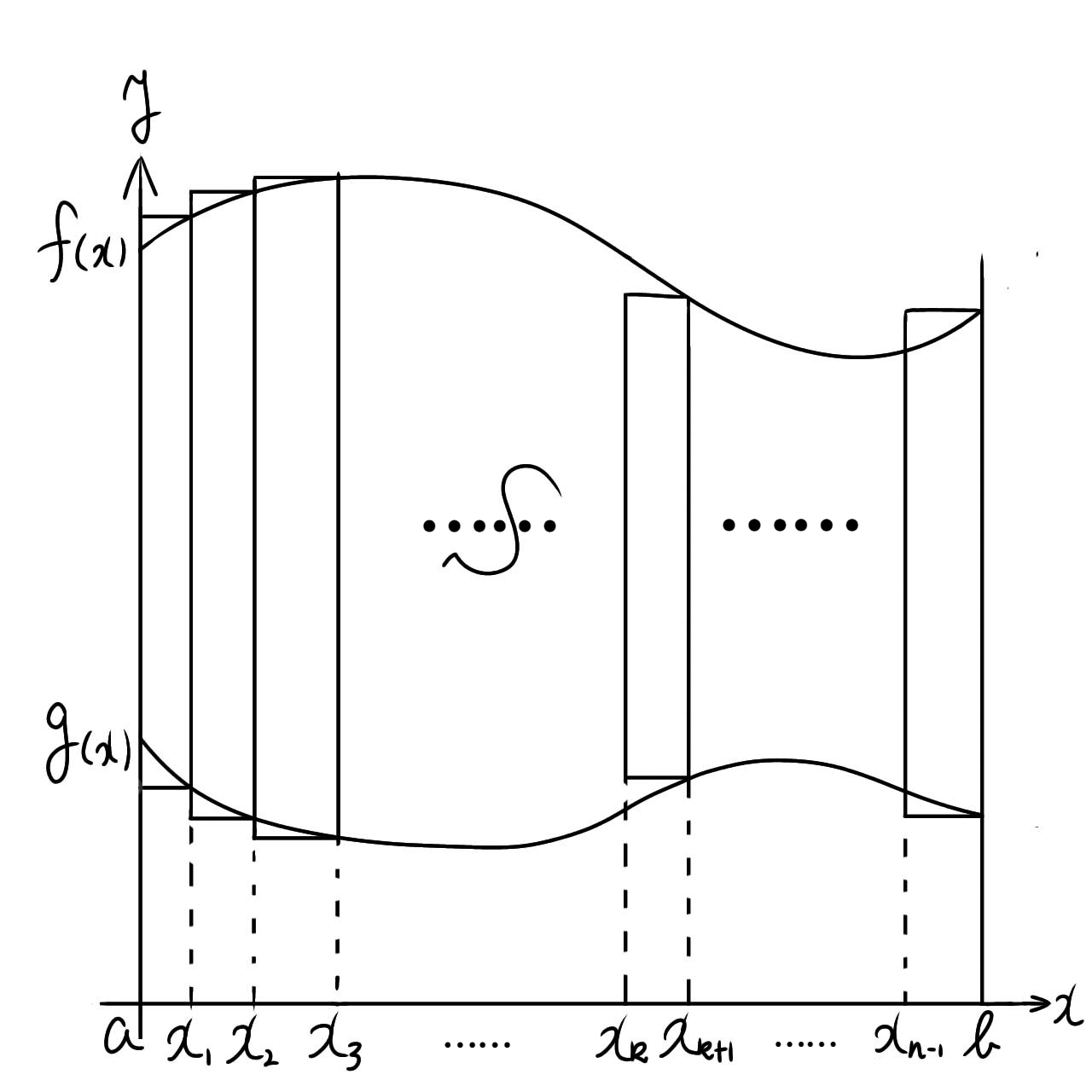
2つの関数 $y=f(x),y=g(x)$ について $x$ の区間 $[a,b]$ における定積分
$$\int_a^b (f(x)-g(x))dx=(F(b)-F(a))-(G(b)-G(a)) \tag{1}$$
を
$$\begin{align*}\int_a^b (f(x)-g(x))dx&=\int_a^b\left(\int_{g(x)}^{f(x)}dy\right)dx\\
&=\int_a^bdx \int_{g(x)}^{f(x)}dy\end{align*} \tag{2}$$
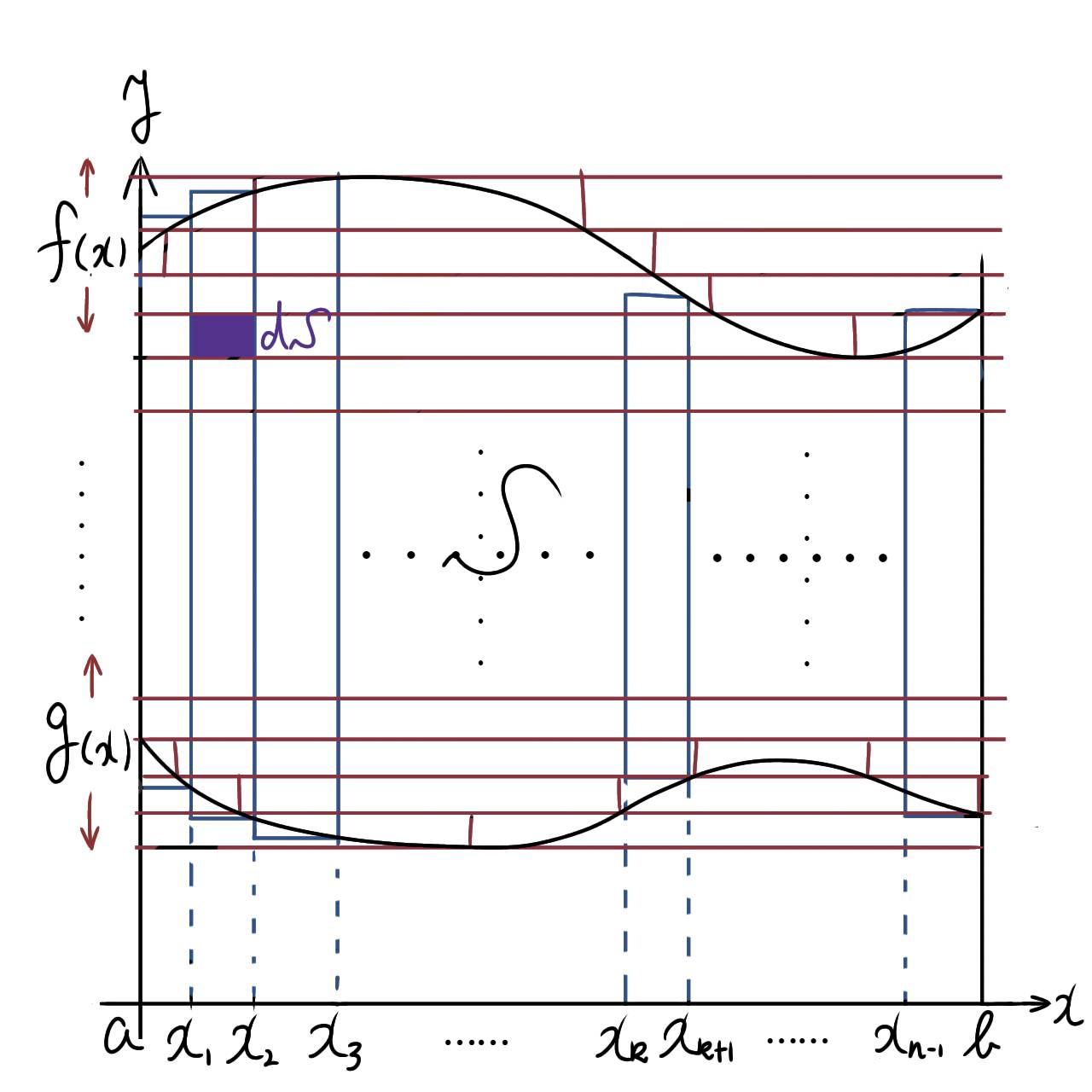
と変形してみる。すると(2)式は区間 $x:[a,b],y:[f(x),g(x)]$ による二重積分と見なせる。この二重積分の被積分関数は定数関数 $h=1$ である。注意しなければならない点は先に $y$ の積分を実行するところであろう。 $y$ の積分について積分区間が変数 $x$ に依存しているから先に $x$ の積分はできないのである。
ここで(2)式について
$$(2)=\int_S dS \tag{3}$$
と置くことにする。この(3)式による積分は $a≤x≤b$ と $y=f(x),y=g(x)$ で囲まれた面 $S$ による積分を表す。以降この領域を $D$ と置き、この面による関数 $h(x,y)=0$ の積分を定義していこう。一般に(3)式による積分とは面による積分という意味合いから面積分と名付けられるという。また定数関数 $h=1$ を被積分関数に持つときには、得られる面積分の結果は $a≤x≤b$ と $y=f(x),y=g(x)$ で囲まれた面積となる。よって積分領域の面積を $S$ と置いて(3)式を
$$S=\int_S dS \tag{3}$$
と書き換えれば、 $dS$ とは面積が $S$ となるような積分領域 $D$ についての微小面素となる。
変数を置換する
そこで変数 $x,y$ を、他の変数 $u,v$ に依存するとすると、各成分の全微分により
$$\begin{align*}
dx_{(u,v)}&=\dfrac{∂x}{∂u} du+\dfrac{∂x}{∂v} dv\\
dy_{(u,v)}&=\dfrac{∂y}{∂u} du+\dfrac{∂y}{∂v} dv
\\
∴ \begin{pmatrix}
dx_{(u,v)}\\
dy_{(u,v)}
\end{pmatrix}
&=
\begin{pmatrix}
\dfrac{∂x}{∂u} & \dfrac{∂x}{∂v}\\
\dfrac{∂y}{∂u} & \dfrac{∂y}{∂v}
\end{pmatrix}
\begin{pmatrix}
du\\dv
\end{pmatrix}
\end{align*}$$
となる。よってヤコビ行列を $\boldsymbol{J}$ と置くと
$$\boldsymbol{J}=\begin{pmatrix}
\dfrac{∂x}{∂u} & \dfrac{∂x}{∂v}\\
\dfrac{∂y}{∂u} & \dfrac{∂y}{∂v}
\end{pmatrix}$$
となる。よって
$$dxdy=|\boldsymbol{J}|dudv$$
となるから、面積分(3)式は
$$(3)=\int_S dS=\iint_D dxdy=\iint_D|\boldsymbol{J}|dudv \tag{4}$$
のように変数 $x,y→u,v$ の置換が可能である。 このヤコビ行列式 $|\boldsymbol{J}|$ とは変数を置換したときに、微小量 $dudv$ がどれだけ微小量 $dxdy$ から拡大されるのか示した量である。
この置換の何が良いのかといえば、面積分において挿入する関数又はベクトルが必ず何かしらの2変数の積分で表されるというところにあるのだ。
一般の場合の面積分はどのように書き表されるのか
さて高校数学で考えてきた積分とは(1)式
$$\int_a^b (f(x)-g(x))dx=(F(b)-F(a))-(G(b)-G(a)) \tag{1}$$
からも分かる通り2次元のデカルト座標系における積分であった。これは $x$ 軸に対して垂直な無限に刻んだ千切り状の微小面を区間 $[a,b]$ に並べたものである。このことから面積分では領域 $D$ 内で面 $S$ に対して垂直に無限にみじん切りした微小面を敷き詰めることになる。よって微小な面素 $dS$ がベクトルとしての量を持つとするのなら、面素ベクトル $d\boldsymbol{S}$ は
$$d\boldsymbol{S}=\boldsymbol{n}dS$$
のように面 $S$ に垂直な単位法線ベクトル $\boldsymbol{n}$ に平行なベクトルとなるはずだ。
確かに面 $S$ が $xy$ 平面による面積分である場合には面素 $dxdy$ による積分となるから、面素ベクトル $d\boldsymbol{S}$ は
$$d\boldsymbol{S}=dxdy\boldsymbol{e}_z$$
となる。これは簡単に分かる。しかし(4)式のように面積分が一般に変数 $u,v$ の積分で置換されるときには少し難しい。まず先に定義したヤコビ行列式 $|\boldsymbol{J}|$ が変数 $u,v$ で表現される面に対して垂直であれば良い。ここで変数 $u,v$ は変数 $x,y$ を置換したものであるから、変数 $u,v$ で表現される面に対して垂直ということは、座標平面 $xy$ に対して垂直であるということである。つまり求める面素ベクトル $d\boldsymbol{S}$ は
$$d\boldsymbol{S}=|\boldsymbol{J}|dudv\boldsymbol{e}_z$$
となる。これをもっと一般の場合のときにも簡単に求めることができれば良いのだが……。
そこでヤコビ行列式 $|\boldsymbol{J}|$ を
$$\begin{align*}\begin{vmatrix}
\dfrac{∂x}{∂u} & \dfrac{∂x}{∂v} & 0\\
\dfrac{∂y}{∂u} & \dfrac{∂y}{∂v} & 0\\
\boldsymbol{e}_u & \boldsymbol{e}_v & \boldsymbol{e}_w
\end{vmatrix}
&=
\left|\hspace{5mm}\begin{matrix}\lower{8mm}\huge\boldsymbol{J}\\\lower{5mm}0\hspace{5mm}\lower{5mm}0\end{matrix}
\hspace{5mm}\begin{matrix}0\\0\\\boldsymbol{e}_w\end{matrix}
\right|\\
&=|\boldsymbol{J}|\boldsymbol{e}_w
\end{align*}\tag{5}$$
と組み込んでみる。すると(5)式は外積を用いて
$$\dfrac{∂\boldsymbol{r}}{∂u}×\dfrac{∂\boldsymbol{r}}{∂v} \tag{6}$$
と書き表される。よって曲面 $S$ の積分領域 $D$ における一般の場合の面積分は
$$\int_S f_{(\boldsymbol{r})}dS=\iint_D f_{(\boldsymbol{r_{(u,v)}})}\left|\dfrac{∂\boldsymbol{r}}{∂u}×\dfrac{∂\boldsymbol{r}}{∂v}\right|dudv \tag{7}$$
のように2つの媒介変数 $u,v$ で表現された関数 $f_{(\boldsymbol{r_{(u,v)}})}$ を挿入することで実現する。また被積分関数がベクトルの場合には(7)式は
$$\int_S \boldsymbol{A}_{(\boldsymbol{r})}d\boldsymbol{S}=\int_S\boldsymbol{A}_{(\boldsymbol{r})}\cdot \boldsymbol{n}dS=\iint_D \boldsymbol{A}_{(\boldsymbol{r_{(u,v)}})}\cdot\left(\dfrac{∂\boldsymbol{r}}{∂u}×\dfrac{∂\boldsymbol{r}}{∂v}\right)dudv \tag{8}$$
のように面素がベクトルとなる。
例)定積分の回転体の体積を求める
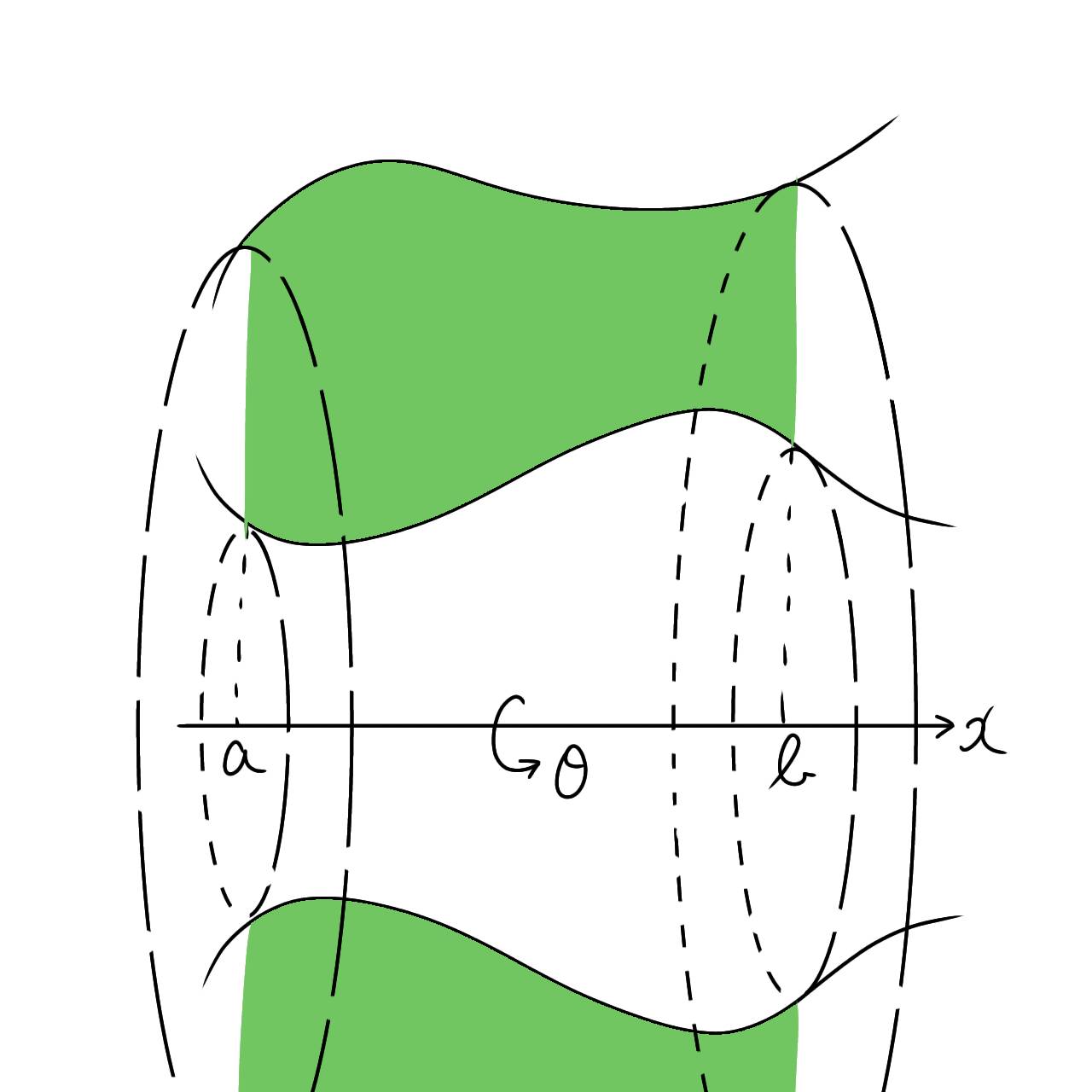
区間 $[a,b]$ による2つの関数 $y=f(x),y=g(x)(ただしいずれも常に正)$ で囲まれる平面の面積は
$$\begin{align*}\int_a^b (f(x)-g(x))dx&=\int_a^b\left(\int_{g(x)}^{f(x)}dy\right)dx\\
&=\int_a^bdx \int_{g(x)}^{f(x)}dy\end{align*} \tag{2}$$
と2変数 $dx,dy$ の面積分で表されるのであった。
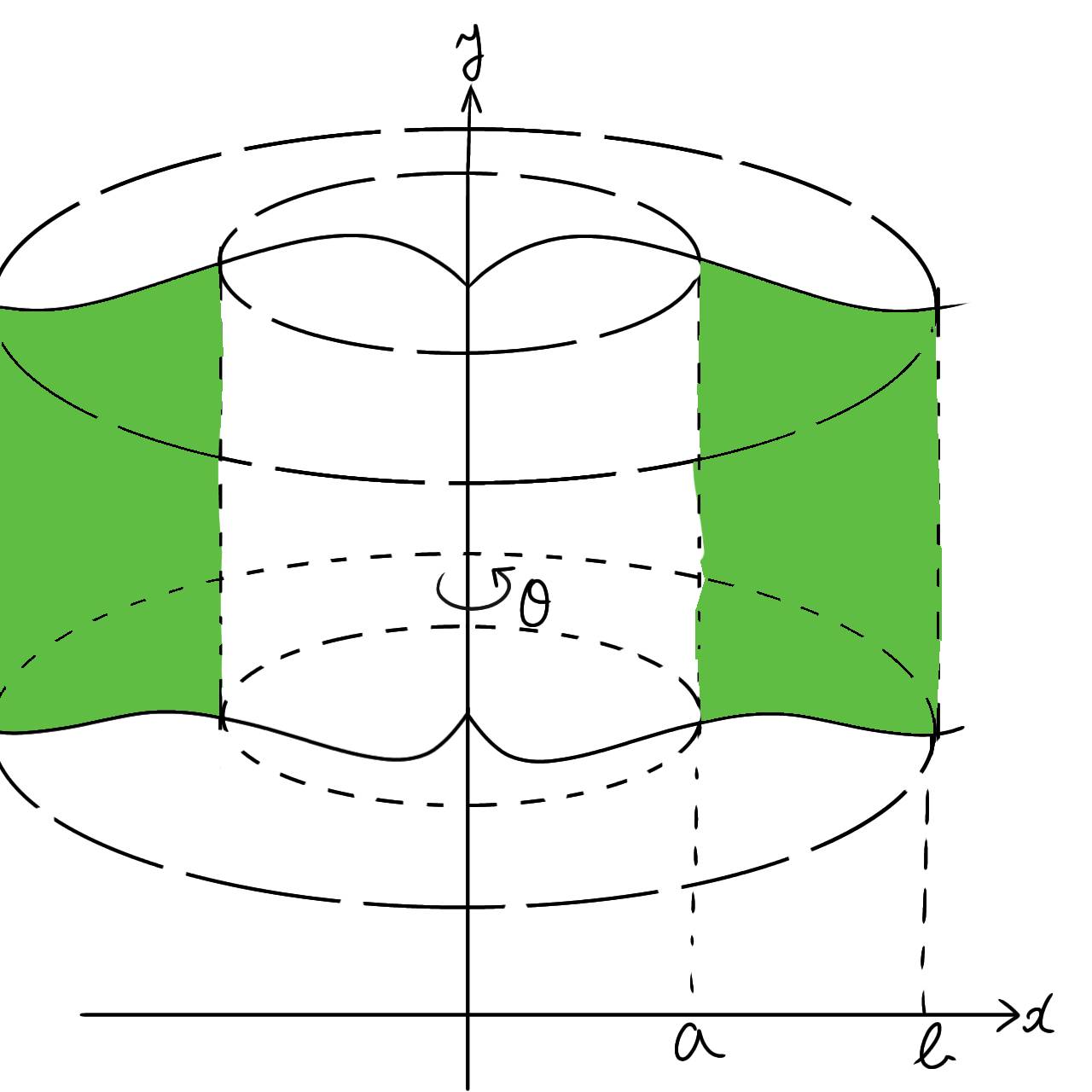
$x$ 軸回りの回転(壺型積分)の場合
そこでもし題意の平面が $x$ 軸回りに回転するのなら、この回転体の体積は
$$\int_a^bdx \iint_{D’}dydz=\int_a^bdx \int_{S’}dS’ \tag{9}$$
のように $x,y,z$ の三重積分で表される。しかし変数 $y,z$ による平面 $S’$ による面積分の積分領域 $D’$ がよく分からないので、何か分かりやすい変数に置換して考えてみたい。
「題意の平面を回転させる」とは丁寧に言えば、「題意の平面を半径と見なして円運動させるように1周回転させる」ということである。つまり $yz$ 平面において円座標系 $(r,θ)$ を取り、 $r$ を $0≤θ≤2π$ だけ回転させれば良い。ただし $θ=0$ のとき $r$ は $xy$ 平面上における平面 $S’$ となる。よって2変数 $y,z$ による面積分は2変数 $r,θ$ に置換させることで上手い具合に計算できそうである。
$$\begin{align*}\begin{pmatrix}
dy\\
dz
\end{pmatrix}
&=
\begin{pmatrix}
\dfrac{∂y}{∂r} & \dfrac{∂y}{∂θ}\\
\dfrac{∂z}{∂r} & \dfrac{∂z}{∂θ}
\end{pmatrix}
\begin{pmatrix}
dr\\dθ
\end{pmatrix}\\
\begin{pmatrix}
dy\\
dz
\end{pmatrix}
&=
\begin{pmatrix}
\cosθ & -r\sinθ\\
\sinθ & r\cosθ
\end{pmatrix}
\begin{pmatrix}
dr\\dθ
\end{pmatrix}\end{align*}$$
であるからヤコビ行列式 $|\boldsymbol{J}|$ は
$$|\boldsymbol{J}|=\begin{vmatrix}
\cosθ & -r\sinθ\\
\sinθ & r\cosθ
\end{vmatrix}
=r$$
となる。よって面素 $dS’$ は
$$dS’=dydz=rdrdθ$$
となる。なお途中のヤコビ行列式は $x$ 成分が任意定数 $C$ の下で $\boldsymbol{r}=(C,r\cosθ,r\sinθ)$ として外積の大きさ
$$\left|\dfrac{∂\boldsymbol{r}}{∂r}×\dfrac{∂\boldsymbol{r}}{∂θ}\right|$$
を計算しても同じことである。
よって(9)式は
$$\begin{align*}
(9)&=\int_b^adx\int_{g(x)}^{f(x)}dr\int_0^{2π}dθ\hspace{1mm}r\\
&=\int_b^adx\hspace{1mm}\frac{1}{2}r^2{\LARGE\left.\right|}_{g(x)}^{f(x)}θ{\LARGE\left.\right|}_0^{2π}
\end{align*} \tag{10}$$
となる。これにより回転角 $θ$ について例えば半回転なら積分の上端は $π$ になるなど、柔軟に対応が可能である。特によくある1回転の回転体の場合には(10)式は
$$(10)=π\int_b^a\left(f(x)^2-g(x)^2\right)dx \tag{11}$$
となる。やったね。高校数学の積分の最後の方に紹介されるような公式が出てきたよ。
$y$ 軸周りの回転(バウムクーヘン型積分)の場合
これも先程と似たような計算をすることになる。ただし異なる点と言えば三重積分で
$$\int_{g(x)}^{f(x)}dy \iint_{D^{\prime\prime}}dzdx=\int_{g(x)}^{f(x)}dy \int_{S^{\prime\prime}}dS^{\prime\prime} \tag{12}$$
のように $zx$ 平面上の平面 $S^{\prime\prime}$ の面積分としているところである。
こちらも先の例と同様に2変数 $y,z$ を2変数 $r,θ$ に置換すれば良い。今回の面素 $dS^{\prime\prime}$ も本当に先と同様に求められるので、良ければ読者も練習と思って導出してみてほしい。
少し気にするところがあるとすれば、定積分 $\displaystyle\int_{g(x)}^{f(x)}dy$ の結果が、恰も $f(x)$ で表される関数を $f(r)$ と単に書き替えただけに見えることくらいか。意外にも疑問に思う人が多いようだが実は単純なことで、 $x$ 軸は回転のときに半径 $r$ として使われるのある。つまり $y=f(x)$ などで表現される $y$ は $y$ 軸回りの回転のときには $x$ を $r$ に書き替えて $y=f(r)$ と表現される。
面素は $dS^{\prime\prime}=rdrdθ$ となるから(12)式は
$$\begin{align*}
(12)&=\int_{g(r)}^{f(r)}dy \int_a^bdr\int_0^{2π}dθ\hspace{1mm}r\\
&=θ{\LARGE\left.\right|}_0^{2π}\int_a^bdr\hspace{1mm}(f(r)-g(r))r
\end{align*} \tag{13}$$
となる。よって1周させる場合には(13)式は
$$2π\int_a^br\hspace{1mm}(f(r)-g(r))dr \tag{14}$$
となる。やったね。なぜかよく分からん極限の挟み撃ちの証明から導出されることが多いバウムクーヘン型積分の公式が出てきたよ。
最後に
本記事では面積分を解説した。しかしどうも面積分は積分の変数を置換したり、面素を求めるために外積やヤコビ行列の知識が必要になるのである。しかし大抵理系の学生は微分積分学と線型代数学の諸計算を学習して習ってまだ慣れないうちに三積分(線積分、面積分、体積分)を学習することになるために、これらの三積分は学生にとってベクトル解析学を学ぶ上で苦手意識を持つ分野の1つとなり得てしまうのだ。特に面積分は抽象的で複雑なイメージを必要とするので大変である。
線積分、面積分、体積分は、数学的な抽象概念ではあるものの、現実的な応用があり、数学や科学の理解に必要な重要な概念であるため、学生は苦手意識を克服するために、継続的な練習と幾何学的なイメージの構築に努める必要があるのだ。
その他面積分の例題
次は線積分も解説しているので是非ご覧あれ



コメント