本シリーズ「マクスウェル方程式で解析する電磁気学」では電磁気学を学習する人が何を何のために求めているのか道を見失わないように、電磁気学で用いられる諸原理、定義を少し丁寧に紹介したつもりです。本シリーズは大学で物理を勉強している学生にとっては当たり前のことばかりではありますが、高校物理の電磁気学を一通り勉強した生徒から大学で電磁気学を学び始めた学生辺りの初学者向けに理解できるような読み物として考えています。
本記事はシリーズ「マクスウェル方程式で解析する電磁気学」の第1部です。電磁気学を成すために必要不可欠なマクスウェル方程式について簡単に紹介しています。
初回
これ
次回
電磁気学で要のマクスウェル方程式
高校物理では電磁気学を学習した。大学の入学試験では殆どの大学が力学、電磁気学で半分以上を占めることもあり、電磁気学は高校物理の中でも力学の次に重要な分野である。
しかし残念なことに高校物理を理解するためには高校レベルを超えた数学の知識が必要になってくるので、仕方なく既知な法則として暗記させるという教育方法を取らざるを得なくなってしまうのだ。
高校物理で学習する電磁気学もその主たる被害者の一人である。電磁気学では各法則(ガウスの方則、アンペールの法則、電磁誘導の法則等)を学んできたが、高校物理ではこれらによって導出された公式を振り回すだけで終わってしまうことも少なくない。各法則が示す意味を知ることができないままただ闇雲に問題を解かされるのである。
いやこれは仕方のないことではある。進学校ならともかく皆が皆高校数学を理解しているわけではないので、彼らに大学数学を教えるとなると教師の骨は粉々である。
確かにこれらの法則を一つに纏まとめることができれば電磁気学の性質を俯瞰的に理解する手掛かりとなりうることだろう。実際マクスウェル方程式は電磁気学の理解に大いに貢献している。この方程式によれば画期的なことに電場と磁場を統一した電磁場の理論として考えることができるのである。つまりマクスウェル方程式を使いこなせるようになれば、高校物理では電磁気学がどうしても電気学と磁気学に区別されることが多かったのを統一的に考えることができ、またマクスウェル方程式に時空論を組み込むことで特殊相対性理論を形成することができるのだ。
マクスウェル方程式の概要
マクスウェル方程式はありがたいことに電磁気学を上手い具合に纏めてくれている。しかし電磁気学はこの方程式を元に解明された訳ではなく、順番的に正しくは古典電磁気学の基礎方程式を見やすく整理したものがマクスウェル方程式なのである。だからといって私達も同じように基礎方程式を考えずにただ闇雲に電磁気学の問題を解くのは余りにも愚行であろう。ここでは折角先人たちによって得られたマクスウェル方程式を美味しく噛み締めることで電磁気学を俯瞰してみよう。
マクスウェル方程式は以下の4式
$$\begin{cases}
\nabla\cdot\boldsymbol{B}=0 \\
\nabla\times\boldsymbol{E}=-\dfrac{∂\boldsymbol{B}}{∂t} \\
\nabla\cdot\boldsymbol{D}=ρ \\
\nabla\times\boldsymbol{H}=\boldsymbol{j}+\dfrac{∂\boldsymbol{D}}{∂t} \\
\end{cases}$$
で構成されている。ただし以下の関係式
$$\begin{cases}
\boldsymbol{D}=ε_0\boldsymbol{E}+\boldsymbol{P}\\
\boldsymbol{H}=\dfrac{1}{μ_0}\boldsymbol{B}-\boldsymbol{M}
\end{cases}$$
が成り立つ。
ここで $\boldsymbol{P}$ は分極、 $\boldsymbol{M}$ は磁化、 $ε_0$ は真空の誘電率、 $μ_0$ は真空の透磁率とする。真空中のときには $\boldsymbol{P}=\boldsymbol{M}=0$ となるが、特に何の断りもない場合には
$$\begin{cases}
\boldsymbol{D}=ε_0\boldsymbol{E}\\
\boldsymbol{H}=\dfrac{1}{μ_0}\boldsymbol{B}
\end{cases}$$
とする。
初学者には何が何だか分からないかもしれないが、勉強すればこれらの式を一瞥するだけで電磁気学の概要がほぼ分かるようになっているので安心してもらいたい。以下ではこれらがどういう意味を示しているのか簡単に紹介している。
磁化保存の式
磁力線は $N$ 極から $S$ 極へ結ばれる(と考えられている)。つまり電磁気学を議論する上で単一の磁荷を持つ何らかの存在(モノポールの存在)を認めないことを前提としているのである。言い換えれば磁荷が湧き出ることはないということなのだ。よって磁場周りの強さを $\boldsymbol{H}$ と置けば
$$\nabla\cdot\boldsymbol{H}=0$$
となるはずである。更に言えば磁束の単位面積当たりの大きさ(磁束密度)を $\boldsymbol{B}$ と置けば
$$\nabla\cdot\boldsymbol{B}=0 \tag{1}$$
とならなければならない。
ファラデーの電磁誘導の法則(による式)
レンツの法則によれば、 $N$ 巻きのコイルを貫く磁場 $\boldsymbol{B}$ が変化するときには磁束 $\Phi$ の変化を打ち消す方向に誘導起電力 $V$ が働き、このとき誘導起電力 $V$ は $N$ に比例する。つまり時間的に変化がある場合には
$$V=-N\dfrac{d\Phi}{dt}$$
となる。これはファラデーの電磁誘導の法則と呼ばれる。特にコイルが1巻きである場合には誘導起電力 $V$ はループ $Γ$ 毎の電場 $\boldsymbol{E}$ の積分によって
$$\oint_Γ\boldsymbol{E}\cdot d\boldsymbol{l}=V$$
となる。よってコイルの巻き数に関係なく
$$\oint_Γ\boldsymbol{E}\cdot d\boldsymbol{l}=-\dfrac{d\Phi}{dt}\tag{2}$$
が成り立つ。また磁束 $d\Phi$ とは空間中の曲面を通り抜ける磁場 $\boldsymbol{B}$ の流束であることから
$$\Phi=\int_S\boldsymbol{B}\cdot d\boldsymbol{S}$$
となる。このとき面 $S$ をループ毎に囲まれる平曲面とすれば、(2)式の左辺はストークスの定理により
$$\oint_Γ\boldsymbol{E}\cdot d\boldsymbol{l}=\int_S(\nabla\times\boldsymbol{E})\cdot d\boldsymbol{S}$$
となる。これにより(2)式は
$$\int_S(\nabla\times\boldsymbol{E})\cdot d\boldsymbol{S}=-\dfrac{∂}{∂t}\int_S\boldsymbol{B}\cdot d\boldsymbol{S} \tag{3}$$
である。よって閉曲面 $S$ が時間変化しない場合には(3)式は
$$\nabla\times\boldsymbol{E}=-\dfrac{∂\boldsymbol{B}}{∂t} \tag{4}$$
となる。ただし今までの閉路 $Γ$ の線積分による表現では、閉路を成す導線が移動する場合には(3)式や(4)式で書き表すことはできないが、ファラデーの電磁誘導の法則はこの場合も包有されることに注意されたい。
ガウスの法則
電気力線は電場の高いところから低いところへ向かう方向に伸びる。これに対して電束 $\Phi$ はある面を貫く電気力線の量のことである。このときある空間における電束 $\Phi$ とは恰もそこに点電荷 $ρ$ があると見做すことができる。
つまり
$$\boldsymbol{\Phi}=ρ\boldsymbol{e}_r$$
を満たす。ここで $\boldsymbol{e}_r$ とは点電荷 $ρ$ から電荷の低い方向へ向かう向きとしている。そのため当然ながら点電荷 $ρ$ から離れた場所では電気力線 $\boldsymbol{\Phi}$ の密度は変化してしまう。
しかしそこで電荷から離れた場所にいても点電荷 $ρ$ を包み込むような閉曲面があれば、点電荷 $ρ$ から伸びる電束で貫くことが可能である。つまりこの電束の量が分かれば点電荷 $ρ$ を知ることができるのだ。
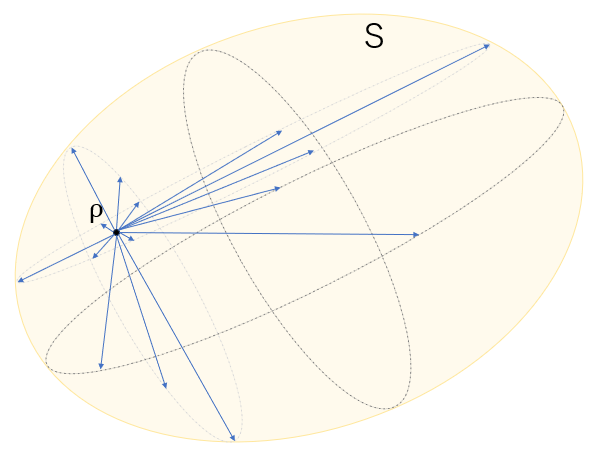
閉曲面を貫く電束の量が分かれば電荷の大きさが分かる
よって電束密度 $\boldsymbol{D}$ は点電荷 $ρ$ を包み込むような閉曲面 $\boldsymbol{S}$ が存在するとき
$$\int_S\boldsymbol{D}\cdot d\boldsymbol{S}=ρ \tag{5}$$
となる。この式の右辺は点電荷としたが、結局考えているのは電束 $\boldsymbol{\Phi}$ の総量なので、考える閉曲面内の空間 $V$ に分布する総電荷 $q$ となる。つまり(5)は
$$\int_S\boldsymbol{D}\cdot d\boldsymbol{S}=\int_Vρ_{(\boldsymbol{r})}d^3r \tag{5亜}$$
となる。(5)、(5亜)式で書かれていることからも分かる通り、電荷 $ρ$ によって磁束密度 $\boldsymbol{D}$ から $ρ$ だけの電気力線が湧き出ると捉えることもできる。つまり(5)、(5亜)式は
$$\nabla\cdot\boldsymbol{D}=ρ \tag{6}$$
と書き替えられるのである。この形を微分形によるガウスの法則と言う。
アンペールの法則$+α$
右ねじの法則というものがあった。電流 $\boldsymbol{I}$ が流れると、その周りに磁場 $\boldsymbol{H}$ が発生するというあれである。これを磁場 $\boldsymbol{H}$ 目線で解釈すれば、磁場 $\boldsymbol{H}$ が1周するところには、それを貫くように電流 $\boldsymbol{I}$ が流れていると言える。よって電流 $\boldsymbol{I}$ を閉路 $C$ で1周するように磁場 $\boldsymbol{H}$ を積分すると、電流 $\boldsymbol{I}$ が得られるはずである。
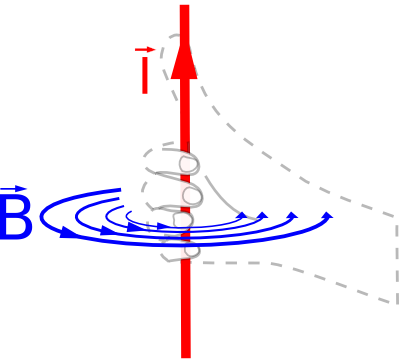
出典:Wiki
つまり
$$\oint_C\boldsymbol{H}\cdot d\boldsymbol{l}=I \tag{7}$$
が成り立つであろう。というのがアンペールの法則である。特に電流は1つだけとは限らず、閉路 $C$ で囲まれる面を $S$ と置くと、(7)式は電流密度 $\boldsymbol{j}$ を用いて
$$\oint_C\boldsymbol{H}\cdot d\boldsymbol{l}=\int_S\boldsymbol{j}_{(\boldsymbol{r})}\cdot d\boldsymbol{S} \tag{7亜}$$
となる。またこれら(7)、(7亜)式からも分かる通り、電流密度 $\boldsymbol{j}$ は磁場 $\boldsymbol{H}$ による回転を受けることで発生すると解釈することができる。つまり(7)、(7亜)式は
$$\nabla\times\boldsymbol{H}=\boldsymbol{j} \tag{8}$$
のようにアンペールの法則を微分形で表すことができる。
しかしこれでは不十分である。なぜなら(8)式の両辺に演算子 $\nabla$ を内積することで、両辺を発散すると、
$$\nabla\cdot(\nabla\times\boldsymbol{H})=\nabla\cdot\boldsymbol{j} \tag{9}$$
となるが、これを計算すると電流密度 $\boldsymbol{j}$ の発散が0であるということになってしまう。これは単純な閉路となる回路(例えば乾電池に繋がれたり、定電圧の電源に接続されていたり)であれば何ら問題ない(正確に言えば導線による効果を考えなくてはならないが、非常に小さいので大抵の場合は無視される)。しかしこれが例えばコンデンサを繋いでいると、このコンデンサ間による変位によって電流が生じるのである。すると当然ながら変位電流によって生じる磁場 $\boldsymbol{H}$ も考慮しなければならなくなるのだ。
よってアンペールの法則は(7亜)式に変位電流の項
$$\dfrac{d}{dt}\int_S\boldsymbol{D}\cdot d\boldsymbol{S}$$
を加える必要がある。よって
$$(7亜)=\oint_C\boldsymbol{H}\cdot d\boldsymbol{l}=\int_S\left(\boldsymbol{j}_{(\boldsymbol{r})}+\dfrac{∂\boldsymbol{D}}{∂t}\right)\cdot d\boldsymbol{S} \tag{10}$$
となる。最後の項は変位電流の項で、面 $S$ が時間に依存しないという仮定の下で(10)式を書いている。よって微分形においては
$$\nabla\times\boldsymbol{H}=\boldsymbol{j}+\dfrac{∂\boldsymbol{D}}{∂t} \tag{11}$$
となる。この式はアンペールの法則をマクスウェルが修正したもので、アンペール・マクスウェルの式等と呼ばれる。
ちょっと休憩
本記事ではマクスウェル方程式を紹介した。電磁気学は体系的に纏めるためにはどうしても高校生にとって高度な数学知識を要する。そのため単に計算させられるだけでよく分からなかった生徒も多いことだろう。本記事は本当に軽く紹介した程度なので、意欲のある生徒は是非学習していくことをお勧めする。
初回
これ
次回



コメント