本記事はシリーズ「マクスウェル方程式で解析する電磁気学」の第3部です。 前回の記事はマクスウェル方程式のうち、第1式と第2式を電磁ポテンシャルを用いて表現できることを示しました。本記事ではローレンツゲージを用いて残りの式についても同様に表現してみます。ローレンツゲージについては相対論的電磁気学の記事で詳しく解説します。
初回
前回
次回
初めて
マクスウェル方程式は電磁気学の基本的な法則を表す方程式であり、電荷や電流がどのように電磁場に作用するかを記述します。一方電磁ポテンシャルは電磁場の表現方法の1つであり、電磁場を電位とベクトルポテンシャルの組み合わせで表現します。
またゲージ変換によって異なる電磁ポテンシャルの組み合わせでもマクスウェル方程式は同じ形をしていることを説明します。特にローレンツゲージと呼ばれる特別なゲージを用いることで、マクスウェル方程式を簡潔に書き表すことができます。またローレンツという名前に因んでローレンツ力についても解説していきます。ローレンツ力ではクーロンゲージというゲージ変換をすることでラプラシアンを用いてかなりシンプルに書き表されます。本記事を読めばクーロンゲージとは性電場になるように要請するためのゲージ変換であることが分かるはずです。
電磁ポテンシャルを用いたマクスウェル方程式
残りの式も電磁ポテンシャルを用いて表現する
前回は試しにマクスウェル方程式の第1,2式を電磁ポテンシャルを用いて
$$\boldsymbol{E}=-\nabla\phi-\dfrac{∂\boldsymbol{A}}{∂t} \tag{17}$$
と書き表すことができることを示した。そこでここでは更にマクスウェル方程式の他の式でもよりすっきりと表現できないか試してみる。
ではマクスウェル方程式
$$\begin{cases}
\nabla\cdot\boldsymbol{B}=0 \\
\nabla\times\boldsymbol{E}=-\dfrac{∂\boldsymbol{B}}{∂t} \\
\nabla\cdot\boldsymbol{D}=ρ \\
\nabla\times\boldsymbol{H}=\boldsymbol{j}+\dfrac{∂\boldsymbol{D}}{∂t} \\
\end{cases}$$
の他の第3,4式も同様に電磁ポテンシャルを用いて表現してみよう。
と、その前に電磁場について以下の関係式
$$\begin{cases}
\boldsymbol{D}=ε_0\boldsymbol{E}+\boldsymbol{P}\\
\boldsymbol{H}=\dfrac{1}{μ_0}\boldsymbol{B}-\boldsymbol{M}
\end{cases}$$
が成り立つことを前提としている。
ここで $\boldsymbol{P}$ は分極、 $\boldsymbol{M}$ は磁化、 $ε_0$ は真空の誘電率、 $μ_0$ は真空の透磁率とする。特に何の断りもない場合には
$$\begin{cases}
\boldsymbol{D}=ε_0\boldsymbol{E}\\
\boldsymbol{H}=\dfrac{1}{μ_0}\boldsymbol{B}
\end{cases}$$
とする。
ではマクスウェル方程式の第3,4式を今までの計算から電磁ポテンシャルで表現すると、
$$\begin{align*}&\begin{cases}
-\Delta\phi-\nabla\cdot\dfrac{∂\boldsymbol{A}}{∂t}=\dfrac{ρ}{ε_0}\\
\left(-\Delta+ε_0μ_0\dfrac{∂^2}{∂t^2}\right)\boldsymbol{A}=μ_0\boldsymbol{j}+\nabla\left(-\nabla\cdot\boldsymbol{A}-ε_0μ_0\dfrac{∂\phi}{∂t}\right)
\end{cases}\\
∴ &\begin{cases}
\left(\Delta-ε_0μ_0\dfrac{∂^2}{∂t^2}\right)\phi+\dfrac{∂}{∂t}\left(\nabla\cdot\boldsymbol{A}+ε_0μ_0\dfrac{∂\phi}{∂t}\right)=-\dfrac{ρ}{ε_0}\\
\left(\Delta-ε_0μ_0\dfrac{∂^2}{∂t^2}\right)\boldsymbol{A}-\nabla\left(\nabla\cdot\boldsymbol{A}+ε_0μ_0\dfrac{∂\phi}{∂t}\right)=-μ_0\boldsymbol{j}
\end{cases}
\end{align*}$$
となる。お、おう……。ところでゲージ変換によれば好きな $\phi,\boldsymbol{A}$ を取ってもマクスウェル方程式の原型は留められるのだった。それなら
$$\nabla\cdot\boldsymbol{A}+ε_0μ_0\dfrac{∂\phi}{∂t}=0 \tag{18}$$
を満たすように $\phi,\boldsymbol{A}$ を定めても良いはずである。一般的にはこのように置かれるゲージをローレンツゲージと言い、(18)式をローレンツ条件と言うのだ。よって(18)式の条件によってマクスウェル方程式の第3,4式は
$$\begin{cases}
\left(\dfrac{1}{c^2}\dfrac{∂^2}{∂t^2}-\Delta\right)\phi=\dfrac{ρ}{ε_0}\\
\left(\dfrac{1}{c^2}\dfrac{∂^2}{∂t^2}-\Delta\right)\boldsymbol{A}=μ_0\boldsymbol{j}
\end{cases} \tag{19}$$
となる。ここで光速 $c$ を $\dfrac{1}{c^2}=ε_0μ_0$ と置いた。更に(19)式はダランベルシアン $\Box$ を用いて
$$\begin{cases}
\Box\phi=\dfrac{ρ}{ε_0}\\
\Box\boldsymbol{A}=μ_0\boldsymbol{j}
\end{cases} \tag{19′}$$
と表現できる。なおダランベルシアン $\Box$ の定義について本記事では
$$\Box:=\dfrac{1}{c^2}\dfrac{∂^2}{∂t^2}-\Delta$$
と定義したが、文献によっては
$$\Box=\Delta-\dfrac{1}{c^2}\dfrac{∂^2}{∂t^2}$$
と定義されることもあるため注意されたい。ダランベルシアン $\Box$ やローレンツゲージについて詳しくは相対論的電磁気学の記事で書く。
ローレンツ力
マクスウェル方程式
$$\begin{cases}
\nabla\cdot\boldsymbol{B}=0 \\
\nabla\times\boldsymbol{E}=-\dfrac{∂\boldsymbol{B}}{∂t} \\
\nabla\cdot\boldsymbol{D}=ρ \\
\nabla\times\boldsymbol{H}=\boldsymbol{j}+\dfrac{∂\boldsymbol{D}}{∂t} \\
\end{cases}$$
の第2式はファラデーの電磁誘導の法則由来の式
$$\nabla\times\boldsymbol{E}=-\dfrac{∂\boldsymbol{B}}{∂t} \tag{4}$$
である。この式は電場と磁場の相互作用を示していて、意味することは
(4)式の左辺によれば電場 $\boldsymbol{E}$ に回転を誘発する渦が存在する場合には、その周りに磁場 $\boldsymbol{B}$ が存在することを示唆している。また右辺からは磁束密度 $\boldsymbol{B}$ の時間的な変化が起きている場合にはそれを打ち消すように電場 $\boldsymbol{E}$ が存在することが分かる。
である。しかしこれではよく分からないのでより詳しく説明しよう。
電場は正の電荷から負の電荷の方向に働き、磁場は $N$ 極から $S$ 極へ伸びる。そこで負の電荷 $-e$ をもった荷電粒子(要するに電子)について考える。
荷電粒子が通過するある場所での垂直な断面積において電荷 $Q$ の流入があるとすると
$$\boldsymbol{I}=\dfrac{d\boldsymbol{Q}}{dt}$$
となる。
ただしこの荷電粒子が速度 $\boldsymbol{v}$ で運動しているとすると、今は $d\boldsymbol{Q}=ed\boldsymbol{r}=e\boldsymbol{v}dt$ であることから電流は電子の流れと逆向きに
$$\boldsymbol{I}=e\boldsymbol{v}$$
となる。
ここでアンペールの法則 $\boldsymbol{B}$ 表記(マクスウェル方程式の第4式の第2項を無視した式)
$$\nabla\times\boldsymbol{B}=μ_0\boldsymbol{j} \tag{8亜}$$
によれば電流の周りには磁場が発生し、ファラデーの電磁誘導の法則由来の式
$$\nabla\times\boldsymbol{E}=-\dfrac{∂\boldsymbol{B}}{∂t} \tag{4}$$
によればその磁場の時間変化を打ち消すような向きに電場が存在する。
(8亜)式について、ベクトルポテンシャル
$$\boldsymbol{B}=\nabla\times\boldsymbol{A} \tag{15}$$
を代入すると
$$\begin{align*}
\nabla\times(\nabla\times\boldsymbol{A})&=μ_0\boldsymbol{j}\\
∴ (\nabla\cdot\boldsymbol{A})\nabla-\Delta\boldsymbol{A}&=μ_0\boldsymbol{j}
\end{align*}$$
となる。ここでクーロンゲージなる
$$\nabla\cdot\boldsymbol{A}=0$$
という条件を考えると、
$$\Delta\boldsymbol{A}=-μ_0\boldsymbol{j} \tag{20}$$
となる。
クーロンゲージとは何か
ちょっと脇道に逸れてクーロンゲージについてその物理的意味を考えてみよう。
クーロンゲージとは
$$\nabla\cdot\boldsymbol{A}=0$$
という条件になるようにゲージ変換したものである。また動電磁場におけるガウスの法則
$$\nabla\cdot\boldsymbol{E}=-\Delta\phi-\dfrac{∂}{∂t}(\nabla\cdot\boldsymbol{A})=\dfrac{ρ}{ε_0}$$
は単なる静電場におけるガウスの法則
$$\Delta\phi=-\dfrac{ρ}{ε_0}$$
となり、これはポアソン方程式である。(20)式やポアソン方程式からも分かる通りクーロンゲージとはマクスウェル方程式に対して静電場になるように要請をするためのゲージ変換であることが分かる。
ビオ・サバールの法則の数学的導出
クーロンゲージを用いて導出した(20)式
$$\Delta\boldsymbol{A}=-μ_0\boldsymbol{j} \tag{20}$$
をグリーン関数やフーリエ変換を使ってベクトルポテンシャル $\boldsymbol{A}$ について解くと
$$\boldsymbol{A}=\dfrac{μ_0}{4π}\int_V\dfrac{\boldsymbol{j_{(\boldsymbol{r})}}}{|\boldsymbol{r}|}d^3\boldsymbol{r}$$
となる。よって磁場 $\boldsymbol{B}$ はベクトルポテンシャルの定義より
$$\begin{align*}
\boldsymbol{B}&=\nabla\times\boldsymbol{A}\\
&=\dfrac{μ_0}{4π}\int\left(\nabla\dfrac{1}{|\boldsymbol{r}’|}\times\boldsymbol{j}_{(\boldsymbol{r}’)}+\dfrac{1}{|\boldsymbol{r}’|}\nabla\times\boldsymbol{j}_{(\boldsymbol{r}’)}\right)d^3\boldsymbol{r}’\\
&=-\dfrac{μ_0}{4π}\int_V\left(\dfrac{1}{|\boldsymbol{r}’|^2}\dfrac{\boldsymbol{r}’}{|\boldsymbol{r}’|}\times\boldsymbol{j}_{(\boldsymbol{r}’)}\right)d^3\boldsymbol{r}’\\
&=\dfrac{μ_0}{4π}\int_V\dfrac{\boldsymbol{j}_{(\boldsymbol{r}’)}\times\boldsymbol{r}’}{|\boldsymbol{r}’|^3}d^3\boldsymbol{r}’ \tag{21}\\
\end{align*}$$
となる。ただし簡単のために原点に観測点を置き、電流が $\boldsymbol{r}’$ の位置にあるとする。また $\boldsymbol{j}$ は電流密度であり、当然ながらこれは回転を誘発する渦を作らないことから
$$\nabla\times\boldsymbol{j}_{(\boldsymbol{r}’)}=0$$
である。(21)式によれば磁場 $\boldsymbol{B}$ は
$$\boldsymbol{j}_{(\boldsymbol{r}’)}\times\boldsymbol{r}’$$
由来の項を持つことから、電流 $\boldsymbol{I}$ の周りに磁場 $\boldsymbol{B}$ が右回りに存在することが分かる。
ローレンツ力の考え方
磁場に方位磁針を向けると、磁場 $\boldsymbol{B}$ の進行方向に磁針が向く(最右図)。普段は北を向いていた磁針が磁場を感知すると、まるで外部からの圧力を受けて整列するかのように皆こぞって磁場 $\boldsymbol{B}$ の進行方向に向く。
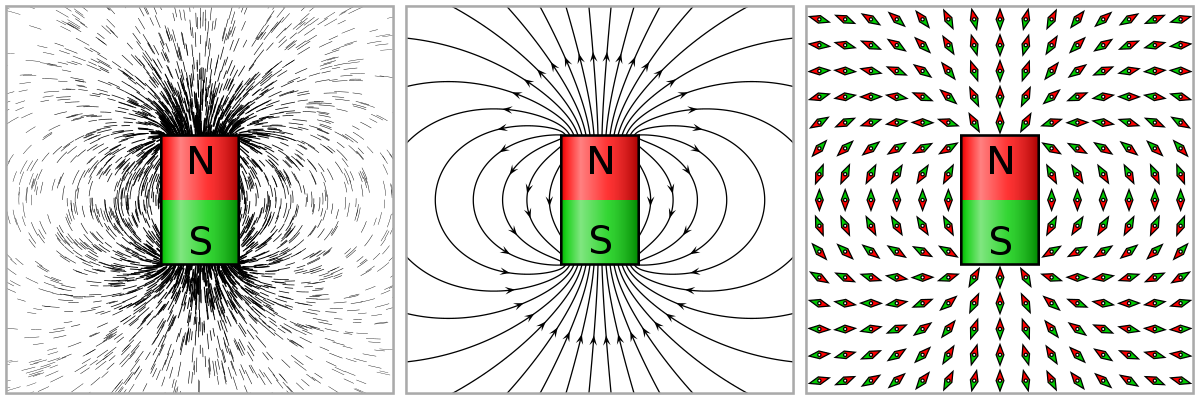
出典:Wiki
では磁場 $\boldsymbol{B}$ に電荷を持つ非常に軽い磁針を置いてちょこっと息を吹きかけたらどうなるのだろうか。つまり初速度を加えるのである。するとそう読者の想像通り磁針は磁場 $\boldsymbol{B}$ の進行方向を向き続ける。この磁針が一定の方向を向くということは当然何かしらの力が働くのである。この力は磁場 $\boldsymbol{B}$ に対して垂直に初速度が与えられているときに最も強く、磁場 $\boldsymbol{B}$ に平行に与えられる場合には元から磁針の向きが磁場 $\boldsymbol{B}$ の進行方向に等しいので、その力は働かないのだ。
実はこの力は速度 $\boldsymbol{v}$ で運動する電荷を $q$ として
$$\boldsymbol{F}_r=q(\boldsymbol{v}\times\boldsymbol{B}) \tag{22}$$
のような力が働くことが知られている。これはローレンツ力(の磁場由来の項)と呼ばれ、運動する荷電粒子に働く力と解釈される。文献によってはローレンツ力を電場由来の項 $\boldsymbol{F}_c$ と磁場由来の項 $\boldsymbol{F}_r$ の重ね合わせとして
$$\begin{align*}
\boldsymbol{F}&=\boldsymbol{F}_c+\boldsymbol{F}_r\\
&=q(\boldsymbol{E}+\boldsymbol{v}\times\boldsymbol{B})
\end{align*}$$
と表される。ここで1つ確認しておきたいのはローレンツ力の仕事を考えてみると
$$\begin{align*}
dW&=\boldsymbol{F}_r\cdot d\boldsymbol{r}\\
&=-q(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{r}\\
&=q(\boldsymbol{v}\times\boldsymbol{B})\cdot \boldsymbol{v}dt\\
&=0
\end{align*} $$
となることである。つまり荷電粒子は磁場による仕事を受けないのだ。
具体的に電流が流れることによって生じる磁場 $\boldsymbol{B}_{out}$ によるローレンツ力は電子の流れによるものである。ここで電子の流れは電流と逆向きである。つまり電子 $-e$ に働くローレンツ力はこの磁場を打ち消すように作用する磁場 $\boldsymbol{B}_{in}=-\boldsymbol{B}_{out}$ によって
$$\begin{align*}\boldsymbol{F}_r&=-e\boldsymbol{v}\times\boldsymbol{B}_{in}\\
&=e\boldsymbol{v}\times\boldsymbol{B}_{out}\\
&=\boldsymbol{I}\times\boldsymbol{B}_{out}\end{align*}$$
と書き表される。
ちょっと休憩
本記事ではマクスウェル方程式を電磁ポテンシャルを用いて書き表した。これによりゲージ変換を施すことで電磁ポテンシャルを一意に定めることができる。本記事ではクーロンゲージとローレンツゲージを紹介したが、次回の記事では他に輻射(又は放射)ゲージを紹介する。相対論的電磁気学の記事ではローレンツゲージについて詳しく説明するので興味がある読者は楽しみにしておいてほしい。
初回
前回
次回



コメント