初めに
本記事はシリーズ「連立方程式の解から束の考え方を導入してみる」の第1部です。本記事ではまずは一次連立方程式の解の判定と、解の種類によってデカルト座標系においてどのように描画されるのか解説していきます。
次回
中学数学では連立方程式は解が定値であるものとされてきましたが、実は一次連立方程式の解は常に定値であるとは限らず、幾つかの媒介変数によって表現されることもあります。本記事では連立方程式を解くために線型代数学の知識が必要になってきますが、具体的な計算は避けて概要を分かるように説明しているので、高校生の読者でも理解しやすいものになっていると思います。
連立一次方程式の解の解析
連立方程式
$$\begin{cases}
x+y=5\\
2x-y=1
\end{cases} \tag{1}$$
の解を求めるためにどのように計算したのであろうか。中学数学では代入法と加減法を習ったことだろう。ここでは連立方程式の計算方法について一旦議論を省くとする。
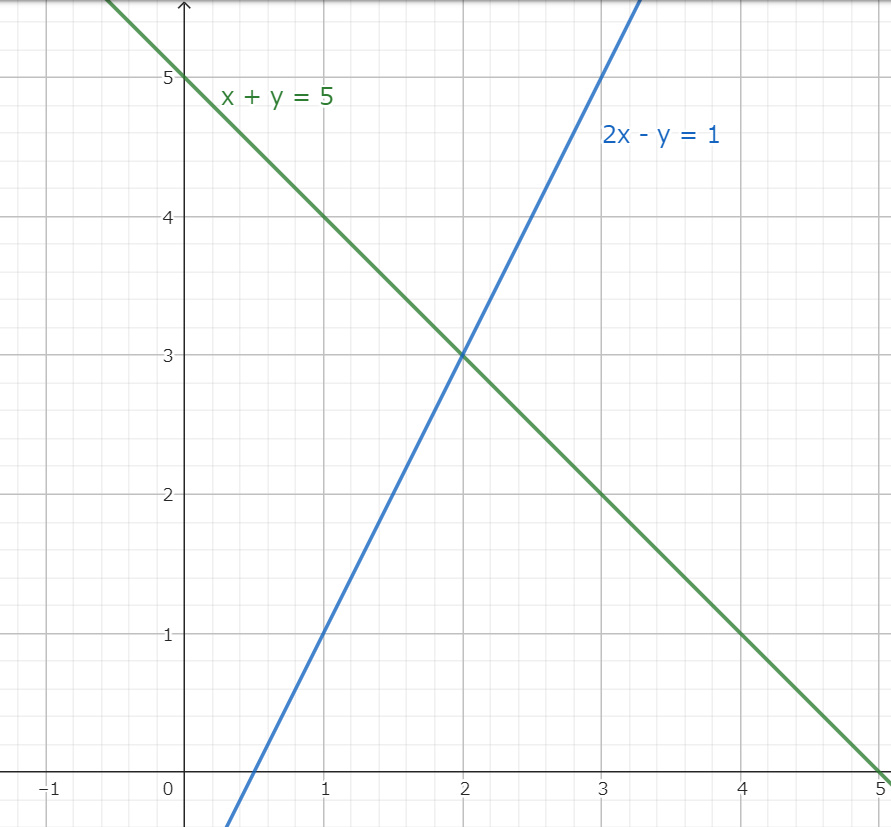
この連立方程式の解は $(x,y)=(2,3)$ である。この連立方程式を解くという操作は上式 $x+y=5$ と下式 $2x-y=1$ を同時に満足する値を求めているのである。この値とはデカルト座標系 $(x,y)$ において2つの直線 $x+y=5, 2x-y=1$ の交点となる。
ところで「連立方程式を解く」もしくは「グラフの交点を求める」操作をするに当たって、手順中に必ず1つ以上の変数を減らすことになる。この1つ以上について詳しく説明しよう。
連立方程式の解の判定
中学数学で解くような連立方程式の解は定値であり、グラフの交点と解釈するのなら定点である。このことは連立方程式(1)を行列を用いることで
$$\begin{align*}
\begin{pmatrix}
1 && 1\\
2 && -1
\end{pmatrix}
\begin{pmatrix}x\\y\end{pmatrix}
&=\begin{pmatrix}5\\1\end{pmatrix}\tag{1}\\
\begin{pmatrix}
1 && 1&& 5\\
2 && -1 && 1
\end{pmatrix}
\begin{pmatrix}x\\y\end{pmatrix}
&=\begin{pmatrix}0\\0\end{pmatrix}\tag{1亜}
\end{align*}$$
のように表現することができる。ただし(1)、(2)で用いた行列をそれぞれ
$$\begin{align*}
A&=
\begin{pmatrix}
1 && 1\\
2 && -1
\end{pmatrix}\\
\tilde{A}&=
\begin{pmatrix}
1 && 1 && 5\\
2 && -1 && 1
\end{pmatrix}
\end{align*}$$
と置き、以下のように列ベクトルを
$$\begin{align*}
\boldsymbol{r}=\begin{pmatrix}x\\y\end{pmatrix}\\
\boldsymbol{c}=\begin{pmatrix}5\\1\end{pmatrix},
\boldsymbol{0}=\begin{pmatrix}0\\0\end{pmatrix}
\end{align*}$$
と置く。すると、連立方程式(1)、(1亜)式は
$$\begin{align*}
A\boldsymbol{r}&=\boldsymbol{c}\tag{1}\\
\tilde{A}\boldsymbol{r}&=\boldsymbol{0}\tag{1亜}
\end{align*}$$
のように行列 $A$ を係数のように見立てた方程式として扱うことができるのだ。この行列 $A$ を係数行列と言い、行列 $\tilde{A}$ を拡大係数行列と言う。この表現の利点は連立2元一次方程式だけではなく、多元一次方程式の場合にも簡潔に書き表すことができる。例えば連立 $n$ 元一次方程式であれば
$$\begin{align*}A&=
\begin{pmatrix}
a_{11} && a_{12} && \cdots && a_{1n}\\
a_{21} && a_{22} && \cdots && a_{2n}\\
\vdots && \vdots && \ddots && \vdots\\
a_{n1} && a_{n2} && \cdots && a_{nn}\\
\end{pmatrix}\\
\tilde{A}&=
\begin{pmatrix}
a_{11} && a_{12} && \cdots && a_{1n} && c_1\\
a_{21} && a_{22} && \cdots && a_{2n} && c_2\\
\vdots && \vdots && \ddots && \vdots && \vdots\\
a_{n1} && a_{n2} && \cdots && a_{nn} && c_n\\
\end{pmatrix}\\
\boldsymbol{r}&=\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix},
\boldsymbol{c}=\begin{pmatrix}c_1\\c_2\\\vdots\\c_n\end{pmatrix}
\end{align*}$$
のように置くことで(1)、(1亜)式として見做すことが可能である。
ここで更に拡大係数行列 $\tilde{A}$ の行を変形する(行基本変形を施す)ことで
$$\tilde{B}=
\begin{pmatrix}
1 && 0 && \cdots && 0 && b_{1,r+1} && \cdots && \cdots && b_{1,n} && d_1\\
0 && 1 && \ddots && \vdots && \vdots && b_{2,r+2} && && \vdots && d_2\\
\vdots && \ddots && \ddots && 0 && \vdots && && \ddots && \vdots && \vdots\\
\vdots && && \ddots && 1 && b_{r,r+1} && \cdots && \cdots && b_{r,n} && d_r\\
0 && \cdots && \cdots && 0 && 0 && \cdots && \cdots && 0 && d_{r+1}\\
\vdots && \ddots && && \vdots && \vdots && \ddots && && \vdots && \vdots\\
\vdots && && \ddots && \vdots && \vdots && && \ddots && \vdots && \vdots\\
0 && \cdots && \cdots && 0 && 0 && \cdots && \cdots && 0 && d_n\\
\end{pmatrix}\tag{2}$$
が得られる。この行列 $\tilde{B}$ は簡約な行列と呼ばれ、簡約な行列を求めることを「行列を簡約化する」と言う。ここでは概要だけを知ってもらうのが目的なので、行列の基本変形延いては行列の簡約化の具体的な手順を説明するのは控える。簡約な行列 $\tilde{B}$ は $r(≤n)$ までは $b_{rr}=1$ となり、それ以降の要素 $b_{ij} (i,j>r)$ は全て $0$ とした。このとき簡約な行列 $\tilde{B}$ は $r$ 階の行列であると言われる。特に $n=r$ のときには簡約な係数行列について $B^{-1}B=E(単位行列)$ となるような逆行列 $B^{-1}$ が存在する。この状態を正則であると言い、この行列を正則行列と言う。
これでは分かりにくいので具体例を見せていこう。連立一次方程式
$$\begin{cases}
\hspace{58px}3x_2+3x_3-2x_4=-4\\
\hspace{10px}x_1+\hspace{10px}x_2+2x_3+3x_4=2\\
\hspace{10px}x_1+2x_2+3x_3+2x_4=1\\
\hspace{10px}x_1+3x_2+4x_3+2x_4=-1
\end{cases}\tag{3}$$
を考える。この連立方程式において拡大係数行列 $\tilde{A}$ を
$$\begin{pmatrix}
0 && 3 && 3 && -2 && -4\\
1 && 1 && 2&& 3 && 2\\
1 && 2 && 3 && 2 && 1\\
1 && 3 && 4 && 2 && -1
\end{pmatrix}$$
と置き、これを簡約化することで連立方程式を解くことができる。簡約化した拡大係数行列は
$$\begin{pmatrix}
1 && 0 && 0 && 1 && 7\\
0 && 1 && 0 && 1 && -2\\
0 && 0 && 1 && 0 && -1\\
0 && 0 && 0 && 0 && 0\\
\end{pmatrix}$$
となる。簡約化された拡大係数行列 $\tilde{B}$ を見て分かる通り、この連立方程式は $3$ 階の行列である。よって連立方程式(3)式の解は
$$\begin{pmatrix}
1 && 0 && 0 && 1 \\
0 && 1 && 0 && 1 \\
0 && 0 && 1 && 0 \\
0 && 0 && 0 && 0 \\
\end{pmatrix}
\begin{pmatrix}x_1\\x_2\\x_4\\x_3\end{pmatrix}=
\begin{pmatrix}7\\-2\\-1\\0\end{pmatrix}
$$
を解くことで求められる。$x_3$ と $x_4$ が入れ替わっているのは、簡約化された拡大係数行列 $\tilde{B}$ を求めるのに第3行と第4行を入れ替えるからである。詳しくは行基本変形を勉強すれば分かるので、気になる読者は勉強しよう。
よって求める解は $x_3=α(任意定数)$ となることに注意して
$$\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}=
\begin{pmatrix}7\\-2\\0\\-1\end{pmatrix}+α
\begin{pmatrix}-1\\-1\\1\\0\end{pmatrix}\tag{4}$$
となる。今回 $x_3=α(任意定数)$ と置いたのは、 $b_{44}=0$ かつ $d_4=0$ より、第4行目が $0=0$ の恒等式となるからである。当然ながら $d_4≠0$ となる場合には常に $0=1$ となってしまい、これを満たす解 $x_3$ は存在しない。よって簡約な拡大係数行列 $\tilde{B}$ (2)式
$$\tilde{B}=
\begin{pmatrix}
1 && 0 && \cdots && 0 && b_{1,r+1} && \cdots && \cdots && b_{1,n} && d_1\\
0 && 1 && \ddots && \vdots && \vdots && b_{2,r+2} && && \vdots && d_2\\
\vdots && \ddots && \ddots && 0 && \vdots && && \ddots && \vdots && \vdots\\
\vdots && && \ddots && 1 && b_{r,r+1} && \cdots && \cdots && b_{r,n} && d_r\\
0 && \cdots && \cdots && 0 && 0 && \cdots && \cdots && 0 && d_{r+1}\\
\vdots && \ddots && && \vdots && \vdots && \ddots && && \vdots && \vdots\\
\vdots && && \ddots && \vdots && \vdots && && \ddots && \vdots && \vdots\\
0 && \cdots && \cdots && 0 && 0 && \cdots && \cdots && 0 && d_n\\
\end{pmatrix}\tag{2}$$
の $(r+1,r+1)$ 以降について、解 $x_i$ は $d_{i}=0$ のときに任意定数 $α_i$ となり、 $d_{i}≠0$ のときには解無しとなる。
デカルト座標系における連立方程式の解の描画
連立方程式(3)式の解(4)は
$$\boldsymbol{v}=\begin{pmatrix}-1\\ 1\\ 1\\ 0\end{pmatrix},
\boldsymbol{P}=\begin{pmatrix}7\\ -2\\ 0\\ -1\end{pmatrix}$$
と置くことで、4次元デカルト座標系 $(x_1,x_2,x_3,x_4)$ において点 $\boldsymbol{v}$ を方向ベクトルとする点 $\boldsymbol{P}$ を通る直線 $\boldsymbol{l}$
$$\boldsymbol{l}=\boldsymbol{P}+α\boldsymbol{v}$$
となる。今回は解の1つが $x_3=α(任意定数)$ であったが、これが例えば解の2つが $α,β(任意定数)$ となるときには連立方程式の解はデカルト座標系において
$$\boldsymbol{l}=\boldsymbol{P}+α\boldsymbol{s}+β\boldsymbol{t}$$
のように平面を表現する。逆に解の内いずれも任意定数となるものが無い場合には連立方程式の解はデカルト座標系において
$$\boldsymbol{l}=\boldsymbol{P}$$
のように定点を表現する。
以上の考察から、連立1元方程式において任意定数の解の個数 $n-r$ は自由度 $n-r$ を表現していて、デカルト座標系においては $n-r$ 次元の図形を描画するのだ。
ちょっと休憩
本記事では連立方程式の解がデカルト座標系においてどのように描画されるのか紹介した。次回では連立方程式から射影幾何学の束の考え方を紹介していく。
次回



コメント