輻射ゲージによる電磁波の解析

本記事はシリーズ「マクスウェル方程式で解析する電磁気学」の第4部となります。第4部では前回解説した電磁ポテンシャルを用いたマクスウェル方程式から、自由空間における波動方程式について解説していきます。

初めに

マクスウェル方程式は電場と磁場の時間変化と空間的な変化を表す偏微分方程式であり、電磁波の振る舞いを記述する基本的な法則です。これにより電場と磁場の相互作用により電磁波が発生し伝搬することがわかります。

特にマクスウェル方程式を解くことにより電磁波がどのように伝搬するかを詳細に解析することができます。また電磁波がどのように反射や屈折するか回折現象が起こる原理など、光学の基礎となる現象を理解するためにもマクスウェル方程式は非常に重要な役割を果たしています。

具体的に磁波、電波はそれぞれ磁束密度 $\boldsymbol{B}$ ,電場 $\boldsymbol{E}$ を用いて

$$\begin{cases} \Delta\boldsymbol{B}-\dfrac{1}{c^2}\dfrac{∂^2\boldsymbol{B}}{∂t^2}=\boldsymbol{0}\\ \Delta\boldsymbol{E}-\dfrac{1}{c^2}\dfrac{∂^2\boldsymbol{E}}{∂t^2}=\boldsymbol{0} \end{cases}$$

と表されます。これらはベクトル場による波動方程式と呼ばれ、解は波の形となります（正確には $\nabla$ により3次元平面波を成す）。

本記事では電磁波の性質を簡単に知るために自由空間における電磁波を調べてみましょう。そのために本記事では電磁ポテンシャルで表現されたマクスウェル方程式に対して輻射ゲージというゲージ変換を施します。これによりクーロンゲージとローレンツゲージを同時に満たすことができ、電磁ポテンシャルの偏微分方程式が単純な波動方程式

$$\dfrac{1}{c^2}\dfrac{∂^2}{∂t^2}\boldsymbol{A}-\Delta\boldsymbol{A}=\boldsymbol{0} \tag{24}$$

に変換されます。ローレンツゲージは次回の特殊相対性理論に関する記事で解説することになりますが、この条件によれば任意の慣性系からの相対的な観測によっても電磁波の伝播速度が一定であることを示しています。クーロンゲージは静電磁場を要請するゲージ変換なので、これら2つのゲージ変換を合わせた輻射ゲージを施すことは、単純に電磁波の性質を知るためには妥当と言えましょう。

マクスウェル方程式から電磁波を解析する

ホイヘンスは1690年に自身の著書『光についての論考』内で回折など光に関する波動としての性質を論じ、それらの性質をホイヘンスの原理と呼ばれる1つの原理に纏め上げた。19世紀後期にはマクスウェル方程式やレンツが行った実験により光が電磁波の一種であり、光は波動であるという見方が強まった。

しかし、それら電磁波についての

1. 波であるとするならば、その媒質は何であるのか
2. マクスウェル方程式からはその速さは一定であるということになるが、互いに運動している観測者の間では相対的にどういうことになるのか

という疑問は後のアインシュタインが発表した特殊相対性理論に関する論文『運動物体の電気力学について』が登場するまでは様々な議論がされていた。これによれば光速はいかなる相対運動をしている観測者からも不変であるということになる。

特殊相対性理論が登場するまでは、宇宙空間にはエーテルと呼ばれる微細な物質が敷き詰められていて、光とはその振動によって伝わるものだと考えられていた。この考え方はローレンツが提唱し、エーテルを基準とした絶対座標系である。これに対しアインシュタインが提唱した特殊相対性理論はその名の通り相対座標系を基準に考えている。そのためアインシュタインは先述の論文でエーテルを含めた絶対座標系による基準を完全に否定することになったのである。またアインシュタインは、真空であっても重力場や電磁場が存在することからこのような空間をエーテルと呼ぶことを提唱した。1つだけ注意されたいことは、アインシュタインによってエーテルの実在性が否定されたのではなく、アインシュタインは長さや時間についての絶対的な基準としてのエーテルを否定したのである。現代ではローレンツかアインシュタインが正しいのかはよく分からずもう宗教上の問題と言えよう。

自由空間における電磁波を調べる

電磁気学における自由空間とは、まあ簡単に言えば真空のようなものである。つまり $ρ,j=0$ とする場合である。このときの電磁場の性質を調べたい。そこで前回導出した電磁ポテンシャルを用いたマクスウェル方程式(19)式,(19′)式

$$\begin{cases} \left(\dfrac{1}{c^2}\dfrac{∂^2}{∂t^2}-\Delta\right)\phi=\dfrac{ρ}{ε_0}\\ \left(\dfrac{1}{c^2}\dfrac{∂^2}{∂t^2}-\Delta\right)\boldsymbol{A}=μ_0\boldsymbol{j} \end{cases} \tag{19}$$

$$\begin{cases} \Box\phi=\dfrac{ρ}{ε_0}\\ \Box\boldsymbol{A}=μ_0\boldsymbol{j} \end{cases} \tag{19′}$$

から、更に以下のようなゲージ変換を施す。

$$\begin{cases} \phi=0\\ \nabla\cdot\boldsymbol{A}=0 \end{cases}$$

このゲージ変換を輻射（又は放射）ゲージと言い、これらの条件を同時に満たすということは、電磁ポテンシャルは

$$\Box\boldsymbol{A}=0 \tag{23}$$

という条件を満たす。つまり輻射ゲージとはクーロンゲージとローレンツゲージを同時に満たすのだ。(23)式は

$$\dfrac{1}{c^2}\dfrac{∂^2}{∂t^2}\boldsymbol{A}-\Delta\boldsymbol{A}=\boldsymbol{0} \tag{24}$$

となり、ベクトルポテンシャル $\boldsymbol{A}$ を求めるにはこの偏微分方程式を解けば良い。この微分方程式の解を $A_{(\boldsymbol{r},t)}=\Theta_{(t)}\Phi_{(\boldsymbol{r})}$ 等と置いて変数分離したりすることで解

$$\boldsymbol{A}_{(\boldsymbol{r},t)}=\boldsymbol{A}_0e^{i(\boldsymbol{k}\cdot\boldsymbol{r}-\omega t)} \tag{25}$$

が得られる。これを見てもよく分からないと思うので一つ一つ説明していく。

波動方程式を解く

まず(24)式を単純化した微分方程式

$$\dfrac{1}{c^2}\dfrac{∂^2}{∂t^2}\boldsymbol{A}-\dfrac{∂^2}{∂x^2}\boldsymbol{A}=\boldsymbol{0} \tag{24亜}$$

について考える。なお(24)、(24亜)式はベクトル $\boldsymbol{A}$ で形成されるベクトル場による微分方程式である。そこで取り敢えずスカラー場であると見做みなしてこの方程式の解を$A_{(x,t)}=\Theta_{(t)}\Phi_{(x)}$ と置いて変数分離によって変数ごとの微分として等式を結ぶと、

$$\dfrac{1}{c^2\Theta_{(t)}}\dfrac{∂^2}{∂t^2}\Theta_{(t)}=\dfrac{1}{\Phi_{(x)}}\dfrac{∂^2}{∂x^2}\Phi_{(x)}=-k^2 \tag{26}$$

のようにある定数 $-k^2　(<0)$ で置くことができる（ $k$ は正負どちらも取りうる）。最右辺を負の定数としたのは天下り的にはなるが、正の定数の場合には波にはならないからである（興味がある読者は調べて見ると良い）。よって(24)式は単純な2つの2階線型斉次微分方程式となり、これらを解くと

$$\begin{align*}&\begin{cases} \Theta_{(t)}=A_t\cos(ckt+τ)\\ \Phi_{(x)}=A_x\cos(kx+α) \end{cases}\\ ∴ &\begin{cases} \Theta_{(t)}=A_t\Re\left[e^{i(ckt+τ)}\right]\\ \Phi_{(x)}=A_x\Re\left[e^{i(kx+α)}\right] \end{cases} \end{align*}$$

となる。ただし $A_t,A_x$ は任意定数としこれは振幅を表す。また $τ,α$ も任意定数としこれは初期位相を表す。上の式の表現は三角関数による表現で、下の式は指数関数による表現である。よって(24亜)式の解は

$$A_{(x,t)}=A_tA_x\Re\left[e^{i(τ+α)}e^{i(kx+ckt)}\right]$$

となる。これにより(24)式の解は3成分 $(x,y,z)$ の波動の重ね合わせであるから

$$\begin{align*} A_{(x,y,z,t)}&=A_t(A_xA_yA_z)\Re\left[e^{i(τ+α+β+γ)}e^{i(k_xx+k_yy+k_zz+ckt)}\right]\\ ∴ A_{(\boldsymbol{r},t)}&=A_tA_\boldsymbol{r}\Re\left[e^{i\phi}e^{i(\boldsymbol{k}\cdot\boldsymbol{r}-\omega t)}\right] \end{align*}$$

のようになる。ただし $i\phi=i(τ+α+β+γ)$ を位相とし $\omega=-ck$ と置き直した。この $\omega$ の置き直しによって $k$ の取りうる値に負号が掛けられる。

ただまあこのままではスカラー場のままであるから、実部虚部関係なく解を複素ベクトルと見なして

$$\begin{align*} \boldsymbol{A}_{(\boldsymbol{r},t)}&=A_tA_\boldsymbol{r}e^{i\phi}e^{i(\boldsymbol{k}\cdot\boldsymbol{r}-\omega t)}\\ &=\boldsymbol{A}_0e^{i(\boldsymbol{k}\cdot\boldsymbol{r}-\omega t)} \tag{25} \end{align*}$$

のように表現すればベクトル場 $\boldsymbol{A}$ の解が得られる。ただし $\boldsymbol{A}_0$ は任意ベクトルとする。得られた解は $\boldsymbol{k}$ を波数ベクトルとする3次元平面波となる。

よって得られた解を

$$\begin{cases} \nabla\cdot\boldsymbol{A}=0\\ \Box\boldsymbol{A}=0 \end{cases}$$

に代入すると、それぞれ

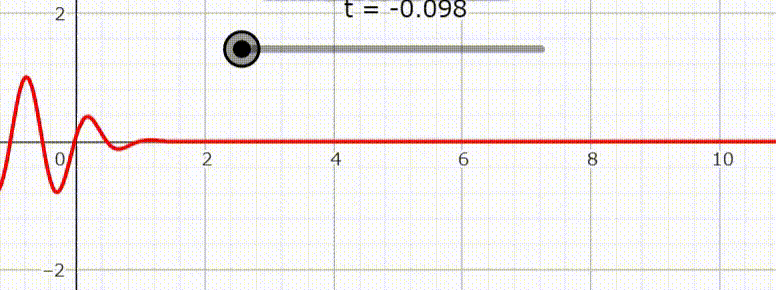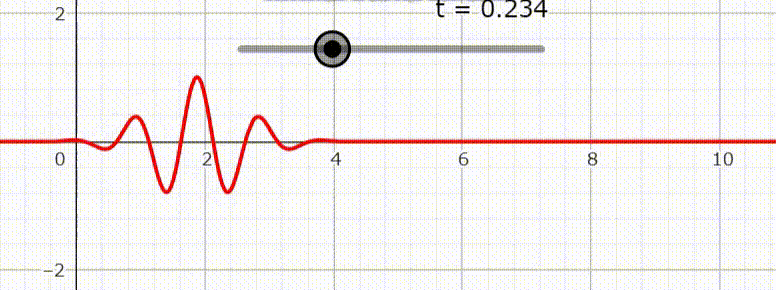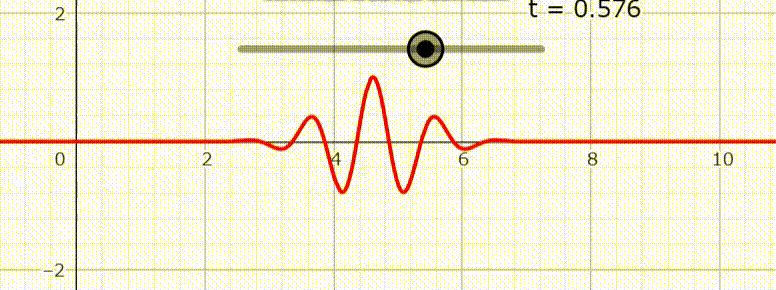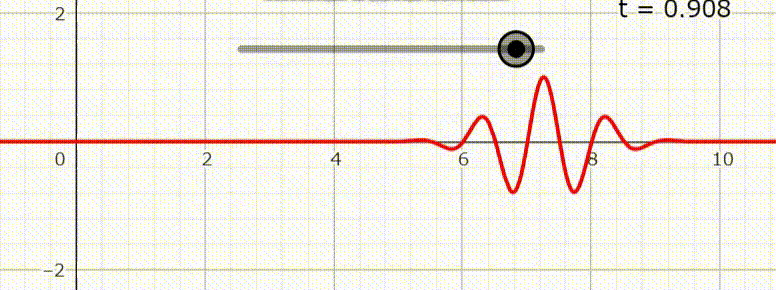
しかしこの結果だけでは $\boldsymbol{A}$ の解としては不十分である。というのも $\boldsymbol{A}$ は実ベクトルであり、また電磁場では一般解は重ね合わせで表現される。

ここで波数ベクトル $\boldsymbol{k}$ に垂直な単位ベクトル $ε_{\boldsymbol{k}σ}　(σ=1,2)$ を

$$ε_{\boldsymbol{k}σ}\cdot ε_{\boldsymbol{k}σ}=δ_{\boldsymbol{k}σ,\boldsymbol{k}σ}$$

と定義する。これを偏光ベクトルと言う。

よってベクトルポテンシャル $\boldsymbol{A}$ の一般解は

$$\boldsymbol{A}_{(\boldsymbol{r},t)}=\sum_{kσ}\left(A_{\boldsymbol{k}σ}ε_{\boldsymbol{k}σ}e^{i(\boldsymbol{k}\cdot\boldsymbol{r}-\omega t)}+A^*_{\boldsymbol{k}σ}ε_{\boldsymbol{k}σ}e^{-i(\boldsymbol{k}\cdot\boldsymbol{r}-\omega t)}\right)$$

となる。ただし $A_{\boldsymbol{k}σ}$ は複素振幅であり、ベクトルポテンシャル $\boldsymbol{A}$ は実ベクトルであるから複素共役を足している。考えるベクトルポテンシャル $\boldsymbol{A}$ が実ベクトルではない場合には第2項は無視される。そこはまあ臨機応変に対応されたい。ベクトルポテンシャル $\boldsymbol{A}$ を求められれば後は

$$\begin{cases} \boldsymbol{E}_{(\boldsymbol{r},t)}=-\dfrac{∂}{∂t}\boldsymbol{A}_{(\boldsymbol{r},t)}\\ \boldsymbol{B}_{(\boldsymbol{r},t)}=\nabla\times\boldsymbol{A}_{(\boldsymbol{r},t)} \end{cases}$$

により電場 $\boldsymbol{E}$ 磁束密度 $\boldsymbol{B}$ を求めることができる。

ちょっと休憩

本記事では自由空間における電磁波の性質を電磁ポテンシャルを用いて簡単に解明してみた。次回では自然な形で相対論的電磁気学の考え方を誘導しよう。