極座標系と極方程式が分からないという声は多く耳にします。しかしそれらの殆どはそもそもベクトルや座標系を理解していないから起こるのです。この問題は高校数学でベクトルの内積がきちんと教えられないところに起因しましょう。内積については以下の記事を参考にしてください。
極座標系とは
極座標系はデカルト座標系と同様に規格化直交系である。
一応確認として任意の単位ベクトル $\boldsymbol{e}_{i}$ によって表現される規格化直交系とは
$$\langle\boldsymbol{e}_{i},\boldsymbol{e}_{j}\rangle=δ_{ij} \tag{1}$$
を満たす( $δ_{ij}$ はクロネッカーのデルタで、 $i=j$ のときには $δ_{ij}=1$ となり、 $i\neq j$ のときには $δ_{ij}=0$ となる)座標系のことを言う。つまり任意の単位ベクトル $\boldsymbol{e}_{i}$ は基底となり、 異なる基底が $i$ 個存在するなら $i$ 次元空間をなす。
さて一般に極座標系における $n$ 次元ベクトルとは1個の動径 $r$ と $n-1$ 個の偏角 $θ_{1},θ_{2},\cdots,θ_{n-1}$ からなる座標系のことである。特に2次元では円座標系、3次元では球座標系となる。3次元の場合には円筒座標系があるが、ここでは特別に指定が無い限りは考えない。
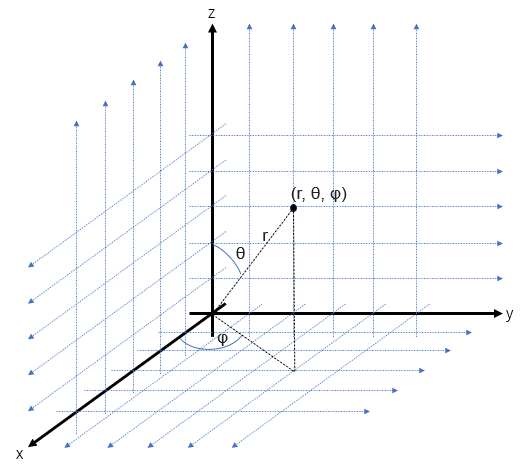
球座標系による座標表示
ところでデカルト座標系においてn次元ベクトル $\vec{x}$ は
$$\vec{x}=\sum_{i=1}^{n} x_{i}\boldsymbol{e}_{i} \tag{2}$$
のように一意的に置かれる(線型独立なベクトルによる線形結合は一意的に定まる)。しかし極座標系では動径 $r$ のn次元ベクトル $\vec{x}$ は
$$\vec{x}=x_{r}\boldsymbol{e}_{x_{r} (θ_1,θ_2,\cdots,θ_{n-1})}+\sum_{j=1}^{n-1} θ_{j}\boldsymbol{e}_{θ_{j} (θ_1,θ_2,\cdots,θ_{n-1})} \tag{3}$$
と表されるだけではなく、その空間対称性から1つの基底を用いて
$$\vec{x}=r\boldsymbol{e}_{r(θ_1,θ_2,\cdots,θ_{n-1})} \tag{4}$$
のように表すことができる。
ここで気を付けたいのは、極座標系の基底は(n-1)個の偏角 $θ_1,θ_2,\cdots,θ_{n-1}$ による依存性が存在することである。その理由は後述で明らかになる。そのため各点における $θ_i$ は当然それぞれ違う。
一般的な極座標系について論じるのはあまりにも抽象的で高校数学内容からかけ離れているので、この記事では2次元極座標系(円座標系)、3次元極座標系(球座標系)を主に書いていく。
円座標系
ここからは円座標系について簡単に解説していく。高校数学で習う極座標系と言えばこれである。円座標系は2次元の極座標系であるから原点からの距離 $r$ の任意の点の位置ベクトルを
$$\boldsymbol{r}=r \boldsymbol{e}_{r(θ)} \tag{5}$$
のように表すことができる。これを高校数学の教科書によくあるような座標として表現すると
$$(r,θ)$$
となる。勿論この点を何か別の偏角 $θ’$ によって
$$\boldsymbol{r}=x_{r}\boldsymbol{e}_{r(θ’)}+x_{θ’}\boldsymbol{e}_{θ'(θ’)} \tag{6}$$
のように2つの基底で表現することも可能である。ただしこの場合の動径 $r$ の大きさは
$$\begin{align*}
r^2=|\boldsymbol{r}|^2=(\boldsymbol{r},\boldsymbol{r})&=x_{r}^2(\boldsymbol{e}{r(θ’)}\cdot\boldsymbol{e}{r(θ’)})+x_{r}x_{θ’}(\boldsymbol{e}{r(θ’)}\cdot\boldsymbol{e}{θ'(θ’)})+x_{θ’}^2(\boldsymbol{e}{θ'(θ’)}\cdot\boldsymbol{e}{θ'(θ’)})\\
&=x_{r}^2+x_{θ’}^2
\end{align*} \tag{7}$$
を満たす。途中の基底同士の積は円座標系が規格化直交系であることから(1)式を満たすことによる。当然のように三平方の定理を使っているわけではないことを知ってほしい。
では具体的に原点からの距離 $r$ の位置ベクトル $\boldsymbol{r}$ について考える。
先の通り円座標系においてベクトルは
$$\boldsymbol{r}=r \boldsymbol{e}_{r(θ)} \tag{8}$$
と表され、一方でデカルト座標系では
$$\boldsymbol{r}=x\boldsymbol{e}_{x}+y\boldsymbol{e}_{y} \tag{9}$$
と表される。
この原点からの距離 $r$ は当然デカルト座標系においても変わらない大きさとなることから、
$$r^2=x^2+y^2 \tag{10}$$
となる。これは正しく円の方程式である。この記事を読んでくれている読者ならお気付きだと思うが(10)式から $x,y$ を $θ$ を用いて
$$\begin{cases}
x=r\cosθ\\
y=r\sinθ
\end{cases} \tag{11}$$
と表される。よって(11)式を(9)式に代入すると
$$\begin{align*}
\boldsymbol{r}=r\cosθ\boldsymbol{e}_{x}+r\sinθ\boldsymbol{e}_{y}&=r(\cosθ\boldsymbol{e}_{x}+\sinθ\boldsymbol{e}_{y})\\
&=r
\begin{pmatrix}
\cosθ & \sinθ
\end{pmatrix} \begin{pmatrix}
\boldsymbol{e}_{x}\\ \boldsymbol{e}_{y}
\end{pmatrix}
\end{align*} \tag{12}$$
となり、これが(8)式と一致することから基底 $\boldsymbol{e}_{r}$ は
$$\boldsymbol{e}_{r_{(θ)}}=
\begin{pmatrix}
\cosθ & \sinθ
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}
\end{pmatrix} \tag{13}$$
となる。よって基底 $\boldsymbol{e}_{θ}$ はこれを $π/2$ だけ回転移動させればよいから
$$\begin{align*}
\boldsymbol{e}_{θ_{(θ)}}&=
\begin{pmatrix}
\cos(θ+π/2) & \sin(θ+π/2)
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}
\end{pmatrix}\\
&=
\begin{pmatrix} -\sinθ & \cosθ
\end{pmatrix}
\begin{pmatrix} \boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}
\end{pmatrix}
\end{align*} \tag{14}$$
となる。従って円座標系の基底 $\langle\boldsymbol{e}_{r_{(θ)}},\boldsymbol{e}_{θ_{(θ)}}\rangle$ は
$$\begin{pmatrix}
\boldsymbol{e}_{r_{(θ)}}\\
\boldsymbol{e}_{θ_{(θ)}}
\end{pmatrix}=
\begin{pmatrix} \cosθ & \sinθ\\
-\sinθ & \cosθ\\
\end{pmatrix} \begin{pmatrix}
\boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}
\end{pmatrix} \tag{15}$$
となる。ただし各基底円座標系の基底 $\langle\boldsymbol{e}_{r_{(θ)}},\boldsymbol{e}_{θ_{(θ)}}\rangle$ が $θ$ (区間 $[0,2π]$)に依存していることに注意されたい。つまり当たり前のことではあるが、同一円周上の点であっても偏角 $θ$ が異なれば基底 $\langle\boldsymbol{e}_{r_{(θ)}},\boldsymbol{e}_{θ_{(θ)}}\rangle$ は異なる。基底 $\boldsymbol{e}_{θ}$ を求めるために基底 $\boldsymbol{e}_{r}$ を $π/2$ だけ回転移動させたが、反対に $-π/2$ でも良いのではと思われる人がいるかもしれない。しかし $π/2$ だけ回転移動させた場合にはデカルト座標系でもよくあるような右手系になるので、特に断りが無ければ $π/2$ だけ回転移動させるのが一般的である。
球座標系
円座標系と同様に3次元位置ベクトル $\boldsymbol{r}$ を
$$\boldsymbol{r}=r \boldsymbol{e}_{r(θ,φ)} \tag{16}$$
と置いたものとデカルト座標系における表示
$$\boldsymbol{r}=x\boldsymbol{e}_{x}+y\boldsymbol{e}_{y}+z\boldsymbol{e}_{z} \tag{17}$$
を比較すれば良い。同じようにこれらの大きさ $r$ を比較すると、
$$r^2=x^2+y^2+z^2 \tag{18}$$
となる。これは球の方程式である。よって $x,y,z$ は $r,θ,φ$ を用いると
$$\begin{cases}
x=r\sinθ\cosφ\\
y=r\sinθ\sinφ\\
z=r\cosθ
\end{cases} \tag{19}$$
と表される。

球座標系による座標表示
よって(17)式、(19)式より
$$\begin{align*}
\boldsymbol{r}&=r\sinθ\cosφ\boldsymbol{e}_{x}+r\sinθ\sinφ\boldsymbol{e}_{y}+r\cosθ\boldsymbol{e}_{z}\\
&=r(\sinθ\cosφ\boldsymbol{e}_{x}+\sinθ\sinφ\boldsymbol{e}_{y}+\cosθ\boldsymbol{e}_{z})\\
&=r
\begin{pmatrix}
\sinθ\cosφ & \sinθ\sinφ & \cosθ
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}\\
\boldsymbol{e}_{z}
\end{pmatrix}
\end{align*} \tag{20}$$
となるから基底 $\boldsymbol{e}_{r_{(θ,φ)}}$ は
$$\boldsymbol{e}_{r_{(θ,φ)}}=
\begin{pmatrix}
\sinθ\cosφ & \sinθ\sinφ & \cosθ
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}\\
\boldsymbol{e}_{z}
\end{pmatrix} \tag{21}$$
となる。よって基底 $\boldsymbol{e}_{θ}$ は基底 $\boldsymbol{e}_{r_{(θ,φ)}}$ から $θ$ 方向に $π/2$ だけ回転移動させれば得られる。
$$\boldsymbol{e}_{θ}=
\boldsymbol{e}_{r_{(θ+π/2,φ)}}=
\begin{pmatrix}
\cosθ\cosφ & \cosθ\sinφ & -\sinθ
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}\\
\boldsymbol{e}_{z}
\end{pmatrix} $$
しかし $φ$ 方向の単位ベクトルについては、求めるのに単に $φ$ 方向に $π/2$ だけ回転移動させるわけにはいかない。(19)式や図1を参考にすれば $φ$ 方向が $xy$平面上の円の回りの向きである(つまり基底 $\boldsymbol{e}_{φ}$ はθに依存しない)ことから、基底 $\boldsymbol{e}_{r_{(θ,φ)}}$ において $θ=π/2$ であることが分かる。
よって基底 $\boldsymbol{e}_{φ}$ は $\boldsymbol{e}_{r_{(θ,φ)}}$ から $φ$ 方向に $π/2$ だけ回転移動させかつ $θ=π/2$ であれば良い。
$$\boldsymbol{e}_{φ}=
\boldsymbol{e}_{r_{(π/2,φ+π/2)}}=
\begin{pmatrix}
\sinφ & \cosφ & 0
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}\\
\boldsymbol{e}_{z}
\end{pmatrix} $$
従って球座標系における各基底 $\langle\boldsymbol{e}_{r_{(θ,φ)}},\boldsymbol{e}_{θ_{(θ,φ)}},\boldsymbol{e}_{φ_{(φ)}}\rangle$ は
$$\begin{pmatrix}
\boldsymbol{e}_{r_{(θ,φ)}}\\
\boldsymbol{e}_{θ_{(θ,φ)}}\\
\boldsymbol{e}_{φ_{(φ)}}
\end{pmatrix}=
\begin{pmatrix} \sinθ\cosφ & \sinθ\sinφ & \cosθ\\
\cosθ\cosφ & \cosθ\sinφ & -\sinθ\\
-\sinφ & \cosφ & 0
\end{pmatrix} \begin{pmatrix}
\boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}\\
\boldsymbol{e}_{z}
\end{pmatrix} \tag{22}$$
となる。
極方程式
方程式とは幾つかの未知数を変数に持つ式のことであり、関数とはある変数(複数あっても良い)が定まるともう一方の変数がただ1つに定まる関係を言う。関数について詳しく知りたい人は写像等で調べられたい。
デカルト座標系で表現されるn変数関数と言えば
$$\begin{cases}
f(x_1,x_2,\cdots,x_n)=0\\
x_n=f(x_1,x_2,\cdots,x_{n-1})
\end{cases} \tag{23}$$
のような形で表され、 $x_1,x_2,\cdots,x_{n-1}$ が全て定まれば、 $x_n$ が一意に定まるものを言う。
一方で極座標系で表現されるn変数関数と言えば
$$\begin{cases}
f(r,θ_1,\cdots,x_{n-1})=0\\
r=f(θ_1,θ_2,\cdots,θ_{n-1})
\end{cases} \tag{24}$$
のような形で表され、 $θ_1,θ_2,\cdots,θ_{n-1}$ が全て定まれば、 $r$ が一意に定まるものを言う。一般的に特に指定が無い限りは $r$ はベクトル $\boldsymbol{r}$ の大きさ $|\boldsymbol{r}|$ を表し $r≥0$ である。
実はここが高校数学の教科書ではあまり語られない内容で生徒を困らせるのだ。高校ではベクトルの存在を一切見せずただ、
一般に極座標 $(r,θ)$ の $r$ は0以上の値であるが、極方程式を考える場合には、 $θ$ の値によっては、 $r$ が負の値をとることもある。このとき、 $(r,θ)$ は極座標 $(│r│,θ+π)$ の点を表すものとする。
高校数学 数学Ⅲ(数研出版)
とあるだけである。この記事で今までやってきたようにベクトル表記 $\boldsymbol{r}$ で書けば、教科書の書かれた内容の意味するところは、単に
$$\begin{align*}
\boldsymbol{r}=r\boldsymbol{e}_{r_{(θ+π)}}&=
r\begin{pmatrix}
\cos(θ+π) & \sin(θ+π)
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}
\end{pmatrix}\\
&=-r\begin{pmatrix}
\cosθ & \sinθ
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{x}\\
\boldsymbol{e}_{y}
\end{pmatrix}\\
&=r\boldsymbol{e}_{r_{(θ)}}\end{align*}
\tag{25}$$
となるということである。
高校数学ではただの計算問題に終わってしまいがちな極方程式だが、当然デカルト座標系と同様に微分・積分等の計算が可能なので、物理学ではしょっちゅう使われる。
終わりに
今回は極座標系と極方程式について少し詳しく解説してみた。高校数学では計算ばかりやらせてそのありがたみはあまり感じられていないと思う。しかし極座標系は動径 $r$ と偏角 $θ$ で表示できることから、物理学では惑星の軌道半径や粒子の軌道半径を計算するのに役に立つ。またデカルト座標系と同様の計算が可能なため、例えば重積分を用いて円の面積や球の体積・表面積をを導出することができるなど球が絡む問題には特に重宝される。



コメント