高校数学では1つの変数による積分をしてきました。その積分する軸を曲線にしてみたというのが線積分です。本記事ではベクトル空間における直線のユークリッド距離から曲線の線積分を考えていこうと思います。
以下の記事でベクトル解析学の三積分(線積分、面積分、体積分)の内の面積分について解説しました。
今回は三積分のうちの線積分を解説していきます。
線積分とは何か
高校数学で登場する定積分とは1変数
$$\int_a^bdx \tag{1}$$
の積分に被積分関数 $f(x)$ を挿入することで実現されるものだった。この積分をデカルト座標系で表現するのなら $x$ 軸に沿った積分となる。(1)式自体は区間 $[a,b]$ における $x$ 軸の距離を表す。当然ながら変数 $y$ の定積分の積分に被積分関数 $f(y)$ を挿入するのなら $y$ 軸に沿った積分となる。では変数 $s$ の定積分の積分に被積分関数 $f(s)$ を挿入するのなら……、そう線 $s$ に沿った積分となるのだ。
つまり(1)式の変数を $x$ から $s$ に変えた
$$l=\int_Cds \tag{2}$$
とは線 $s$ 上の区間 $C$ の距離 $l$ となる。よって $ds$ は線 $s$ の距離を形成する微小な線素である。これを線による積分という意味合いから線積分と名付けよう。
出典:Wiki
では線素がベクトル $d\boldsymbol{s}$ となる場合には、この単位ベクトルはどうなるのだろうか。
まあそう悩むことではなかろう。線 $s$ に沿って積分するのだから、挿入する被積分ベクトルは線 $s$ にどれだけ従属かによるはずだ。よって線素は線 $s$ の単位ベクトル $\boldsymbol{e}_s$ を用いて
$$d\boldsymbol{s}=\boldsymbol{e}_sds$$
と表されるのである。これと被積分ベクトルとの内積を取れば良い。
といってもこれでは $ds$ がよく分からないのであまり使い勝手が良くない。そこで線が $s=r(t)$ のように変数 $t$ で表現されているものとしてみよう。ベクトルの場合には $\boldsymbol{s}=s\boldsymbol{e}_s=\boldsymbol{r}(t)$ である。このとき $d\boldsymbol{s}$ は全微分により
$$d\boldsymbol{s}=\frac{∂\boldsymbol{r}}{∂t}dt$$
と表される。よって(2)式は
$$(2)=\int_C\frac{∂\boldsymbol{r}}{∂t}dt \tag{3}$$
となる。よって線積分は
$$\int_Cf_{(\boldsymbol{r}_{(t)})}\left|\frac{∂\boldsymbol{r}}{∂t}\right|dt \tag{4}$$
のように1変数 $t$ で表される関数 $f(\boldsymbol{r}_{(t)})$ を挿入することで実現する。また被積分関数がベクトルの場合には(4)式は
$$\int_C\boldsymbol{A}_{(\boldsymbol{r}_{(t)})}\cdot\frac{∂\boldsymbol{r}}{∂t}dt \tag{5}$$
となる。
ベクトル空間における線積分
とはいえ(4)、(5)式のままではまだ実用的とは言えないので、より具体的にベクトル空間における線積分を考えてみる。
曲線の長さはどうなるのか
直線の距離
$n$ 次元ベクトル空間の任意の点 $\boldsymbol{r}$ は、 $n$ 個の基底の線型結合によって
$$\boldsymbol{r}=\sum_{k=1}^nx_k\boldsymbol{e}_k$$
のように表される。よって2点 $\boldsymbol{r}_a,\boldsymbol{r}_b$ を結ぶ線分 $\boldsymbol{r}_{ab}$ は
$$\boldsymbol{r}_{ab}=\boldsymbol{r}_b-\boldsymbol{r}_a=\sum_{k=1}^n(x_{bk}-x_{ak})\boldsymbol{e}_k \tag{6}$$
となる。ここで線分 $\boldsymbol{r}_{ab}$ は点$\boldsymbol{r}_a$ による点 $\boldsymbol{r}_b$ 方向への単位ベクトル $\boldsymbol{e}_{\boldsymbol{r}_{ab}}$ の線型結合 $r\boldsymbol{e}_{\boldsymbol{r}_{ab}}$ で表される。つまり(6)式は
$$\boldsymbol{r}_{ab}=\boldsymbol{r}_{ab}\boldsymbol{e}_{\boldsymbol{r}_{ab}}=r\dfrac{\boldsymbol{r}_{ab}}{r}$$
と書き替えられるのである。よって線素 $d\boldsymbol{s}$ は $d\boldsymbol{s}=\boldsymbol{e}_{\boldsymbol{r}_{ab}}ds$ となり、線分 $\boldsymbol{r}$ と同一の単位ベクトルの線型結合で表される(図形的には平行)。このとき $r$ とは線分 $\boldsymbol{r}$ の大きさ $|\boldsymbol{r}|$ となる。
ところで $r$ は
$$\begin{align*}r^2=|\boldsymbol{r}|^2&=\boldsymbol{r}^*\cdot\boldsymbol{r}\\
&=\sum_{k=1}^n|x_{bk}-x_{ak}|^2
\end{align*}$$
より
$$r=\sqrt{\sum_{k=1}^n|x_{bk}-x_{ak}|^2} \tag{7}$$
となる。よってベクトル空間における直線の距離(ユークリッド距離)は
$$\begin{align*}
\boldsymbol{s}=s\boldsymbol{e}_{\boldsymbol{r}_{ab}}&=\sqrt{\sum_{k=1}^n|x_{bk}-x_{ak}|^2}\boldsymbol{e}_{\boldsymbol{r}_{ab}}\\
&=\sum_{k=1}^n(x_{bk}-x_{ak})\boldsymbol{e}_k
\end{align*} \tag{8}$$
となる。右辺上式は1つの基底で表現しているため線素がスカラーの場合に役に立ち、下式は基底 $\boldsymbol{e}_k$ が変数に依存しないため、変数 $t$ の変化量を調べるのに各成分ごとに考えることができる。
曲線の線積分
(8)式が微小に変化する場合には $d(x_{bk}-x_{ak})=dx_k$ と置いて
$$d\boldsymbol{s}=\sum_{k=1}^ndx_k\boldsymbol{e}_k \tag{9}$$
となる。これが無限に並べられれば線を形成する。しかし単に
$$\int_{x_a}^{x_b}d\boldsymbol{s}=\int_{x_a}^{x_b}\sum_{k=1}^ndx_k\boldsymbol{e}_k \tag{10}$$
と積分して終わらせてしまうのは、結局元の直線となってしまいそれでは面白くなかろう。そこで各成分の係数 $x_k$ が1つの変数 $t$ で媒介されているとしよう。このとき(9)式は全微分により
$$d\boldsymbol{s}=dt\sum_{k=1}^n\frac{dx_k}{dt}\boldsymbol{e}_k \tag{9}$$
と書き替えられる。これを無限に並べれば曲線を形成することができよう。よって曲線 $\boldsymbol{s}$ の線素 $d\boldsymbol{s}$ は
$$d\boldsymbol{s}=dt\sum_{k=1}^n\frac{dx_k}{dt}\boldsymbol{e}_k \tag{9}$$
であり、これを無限に並べたもの
$$\int_{x_a}^{x_b}d\boldsymbol{s}=\int_{x_a}^{x_b}dt\sum_{k=1}^n\frac{dx_k}{dt}\boldsymbol{e}_k \tag{11}$$
は曲線 $\boldsymbol{s}$ の区間 $[x_a,x_b]$ における長さ $\boldsymbol{l}$ (ベクトル)を表す。長さ $l$ (大きさ)を求める場合には(11)式を変形しても良いが、(8)式の右辺上式
$$\sqrt{\sum_{k=1}^n|x_{bk}-x_{ak}|^2}\boldsymbol{e}_{\boldsymbol{r}_{ab}}$$
を利用して
$$\int_{x_a}^{x_b}ds=\int_{x_a}^{x_b}dt\sqrt{\sum_{k=1}^n\left|\frac{dx_k}{dt}\right|^2} \tag{12}$$
となる。線積分をする場合には(11)、(12)式にそれぞれ被積分ベクトル、被積分関数を挿入することで実現する。
複素数平面による線積分
今までの議論は実・複素を指定せずにベクトル空間における直線の距離から曲線の長さを考えてきた。特に実ベクトル空間においては高校生にも馴染みのあるユークリッド空間における議論となる。具体的に3次元 $(n=3)$ のときにはデカルト座標系で点が $(x,y,z)$ と表され、2次元 $(n=2)$ のときにはデカルト座標系で点が $(x,y)$ と表される。そこでより具体的に複素1次元ベクトル空間における線積分を考えてみたい。なぜこんなにも具体的に考えるのかといえば、複素1次元ベクトル空間における議論がそのまま複素数平面において視覚的に理解することができるからである。よって複素数平面における線積分(複素線積分)を解析的に解釈することができるのである。
とは言え別に難しいことを話しているわけではない。ここでは複素数平面の線積分における主定理であるコーシーの積分定理を例に挙げて複素数平面の線積分を解析的に見ていこうと思う。この定理は簡単に言えば、
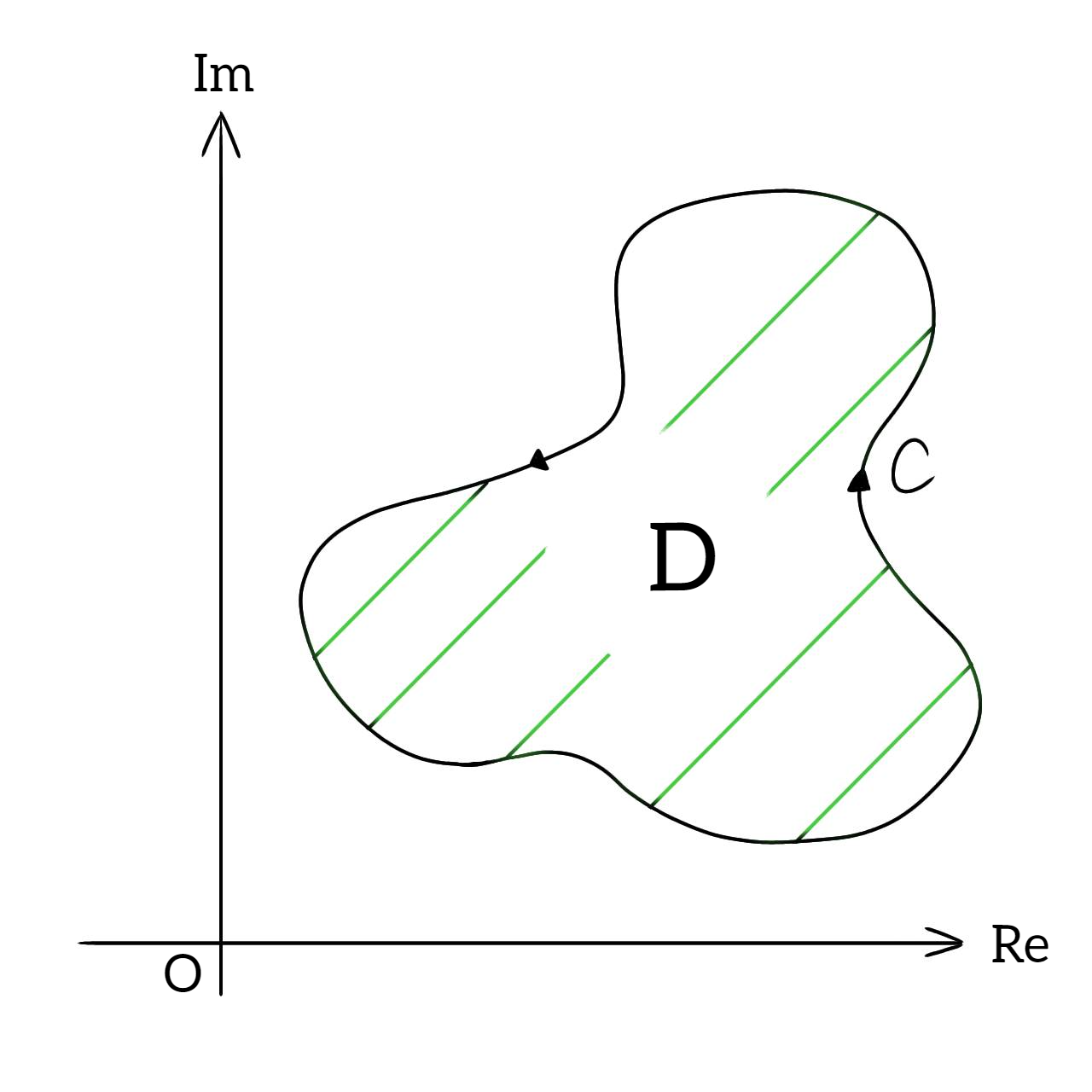
コーシーの積分定理交差しない閉曲線 $C$ によって1つの領域 $D$ だけを包み込み、複素関数 $f(z)$ がこの領域 $D$ 上で常に微分可能であるとする。このときこの閉路 $C$ における複素線積分は
$$\oint_Cf(z)dz=0$$
となる。
複素数平面における線積分の閉路 $C$ と、その内部にある領域 $D$
というものである。複素数平面で考えると不思議な感じがするかもしれないが、実は単純な話で、私達は既にその性質を知っているのである。
そこで実空間における実関数 $f(x)$ の $x$ による積分
$$\int f(x)dx$$
を考えてみる。この積分が積分区間 $[a,a]$ の定積分で表されるのなら、
$$\begin{align*}
\oint_a^af(x)dx&=\int_a^bf(x)dx+\int_b^af(x)dx\\
&=\int_a^{a_1}f(x)dx+\int_{a_1}^{a_2}f(x)dx+\cdots+\int_{a_2}^{a_1}f(x)dx+\int_{a_1}^af(x)dx\\
&=0\end{align*}$$
となり、実数直線においては積分経路が折り返した直線のみになってしまう。しかし複素数平面であれば積分経路は自由に閉路を描くことができる。どちらも1次元のベクトル空間(数)ではあるが、複素ベクトルの場合には複素数を実部、虚部を分離して係数が実数であるような平面 $(\mathbb{R}^2)$ で考えることができるのである。

つまり複素線積分は複素関数 $f(z)$ を実変数 $t$ を用いて
$$f_{(z)}=u_{(t)}+iv_{(t)}$$
のように実部と虚部とで分離することができるのである。このときの経路 $C$ における複素積分は
$$\begin{align*}
\int_Cf_{(z)}dz&=\int_Cf_{(z_{(t)})}\frac{dz}{dt}dt\\
&=\int_C(u_{(t)}+iv_{(t)})\frac{dz}{dt}dt\\
&=\int_Cu_{(t)}\frac{dz}{dt}dt+i\int_Cv_{(t)}\frac{dz}{dt}dt
\end{align*}$$
となり、実部と虚部共に同一の実変数 $t$ の積分で書き表されるのだ。
最後に
本記事ではベクトル空間における線積分を紹介した。最後の方は複素線積分も紹介している。線積分は面積分と同様にベクトル解析学において学生が躓く分野である。線積分は1つの変数で積分するため面積分ほどの煩雑さは無いが、しかしそれでも体積分といった単純な重積分と比較すると難しいと感じてしまうことだろう。ベクトル三積分(線積分、面積分、体積分)は数学以外にも統計学や他の自然科学の分野にも応用されるので、理解しておきたい分野である。



コメント