本記事はシリーズ「ルジャンドル変換の多面的な理解」の第1部になります。第1部では、ルジャンドル変換 $f^*(p)$ の定義に自然と繋げるために接線の方程式を線座標系で表現してみます。
次回
前書き
本記事では、ルジャンドル変換という数学的な手法について説明しています。ルジャンドル変換とはある関数に対して、その傾きを変数とした別の関数を定義することです。この変換は最適化問題や熱力学などの分野で応用されるのですが、初学者にとってはこの変換を理解するのに苦労することだと思います。本記事ではまずルジャンドル変換の定義に導くために、接線の方程式を線座標系で表現する方法を紹介します。
接線の方程式からルジャンドル変換へ
変数 $x,y$ がある関数 $F(x,y)=0$ によって制約を受けているとし、この関数は考える定義域内で凸関数で点 $\boldsymbol{r}$ 付近では滑らかであるとする。このとき関数 $F(x,y)=0$ 上の点 $\boldsymbol{r}=(x_0,y_0)$ を接点とするように接平面 $α$ を取る。この点 $\boldsymbol{r}$ と接平面 $α$ 上の $\boldsymbol{r}$ を除く任意の点 $\boldsymbol{a}=(x,y)$ とを結ぶベクトル $\boldsymbol{a}-\boldsymbol{r}$ は、デカルト座標系($xy$ 平面)において曲線 $F(x,y)=0$ 上の点 $\boldsymbol{r}$ における接ベクトルとなる。よって点 $\boldsymbol{r}$ における接線の方程式 $l$ は
$$\begin{align*}
l:\nabla F(\boldsymbol{r}) \cdot (\boldsymbol{a}-\boldsymbol{r})=0\\
∴\dfrac{∂F(\boldsymbol{r})}{∂x} (x-x_0)+\dfrac{∂F(\boldsymbol{r})}{∂y} (y-y_0)=0\end{align*}$$
$$\begin{align*}
∴y-y_0&=-\dfrac{∂F(\boldsymbol{r})}{∂x}\dfrac{∂y}{∂F(\boldsymbol{r})} (x-x_0)\\
&=-\dfrac{dy(x_0)}{dx} (x-x_0)\\
∴{}y&=-\dfrac{dy(x_0)}{dx} x+\left(\dfrac{dy(x_0)}{dx} x_0+y_0\right)\\
&=-\dfrac{dy(x_0)}{dx} x+\left(\dfrac{dy(x_0)}{dx} x_0+y_0\right)\tag{1}
\end{align*}$$
となる。
最初の $\nabla f$ は法線ベクトルを求めている。なぜか疑問に思った読者はこちら
を参考にされたい。
得られた直線の方程式(1)は単に陰関数 $F(x,y)=0$ を式変形したものである。見慣れた直線の方程式にするには、ここで陽関数 $y=f(x)$ が $F(x,y)=f(x)-y=0$ と陰関数表示されることを利用する。よって変数 $y$ について $\dfrac{dy}{dx}→-\dfrac{dy}{dx}$ と置き、微分係数を $\dfrac{dy(x_0)}{dx}→f'(x_0)$ と置くことで、陽関数における接線の方程式
$$l:y=f'(x_0)x-\left(f'(x_0)x_0-f(x_0)\right)\tag{2}$$
を得る。
ここで右辺第2項以下について $p=f'(x_0)$ として
$$\begin{align*}
f^*&=f'(x_0)x_0-f(x_0)\\
∴f^*(p)&=px_0-f(x_0)
\end{align*}\tag{3}$$
と置いてみる。この関数(のような) $f^*(p)$ を(2)式に代入して
$$l:y=px-f^*(p)\tag{4}$$
のように表現すると、直線 $l$ は $p$ を傾きとし、 $-f^*(p)$ を $y$ 切片とする直線と言える。
ここで接線 $l$ を陽関数における線座標系 $(傾き,y切片)$ で表現してみると、接線 $l$ は
$$l:(p,-f^*(p)) \tag{5}$$
と表わされる。この表現は直線 $l$ の傾きを変数として $y$ 切片を記述するというものだ。
線座標についてはこちら
そこで $y$ 切片で使用される
$$f^*(p)=px_0-f(x_0) \tag{3}$$
について、直線 $l$ が関数 $y=f(x)$ 上の点 $\boldsymbol{r}=(x_0,y_0)$ における接線であれば $p=f'(x_0)$ となる。
また関数 $y=f(x)$ が滑らかな凸関数であるから、 $p≶f'(x)$ のときに直線 $l$ は周辺で2個共有点を持つ。つまり直線 $l$ が関数 $y=f(x)$ における接線である場合には
$$\begin{align*}&f^*(p)=px-f(x)\\ &\quad at\ x\ such\ that\ f'(x-0)≤p≤f'(x+0)\end{align*}\tag{6}$$
を満たすように傾き $p$ を定めるということになる。ここで $x$ とは滑らかな凸関数 $y=f(x)$ の点の $x$ 座標のことである。この式が意味するところは変数 $x$ が接点の $x$ 座標になるように傾き $p$ を定めるということである。
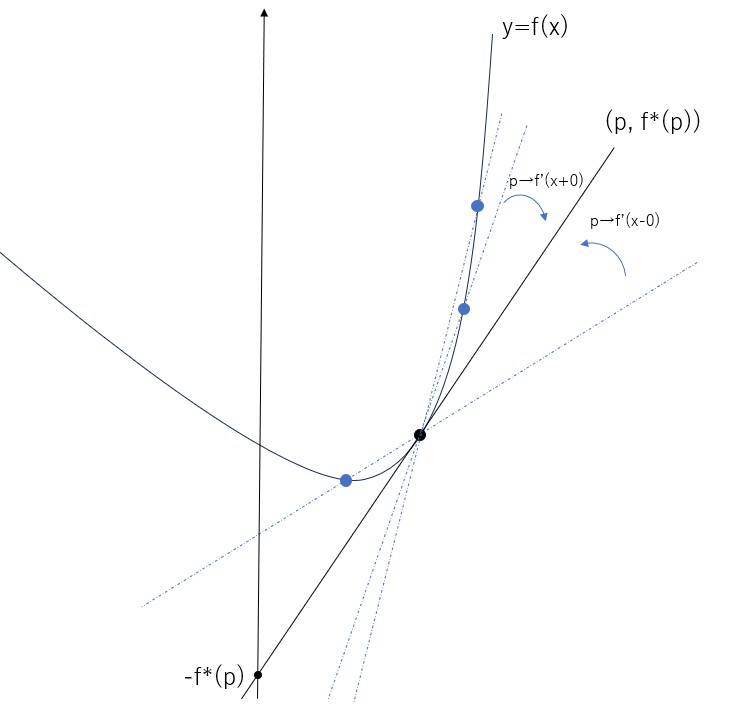
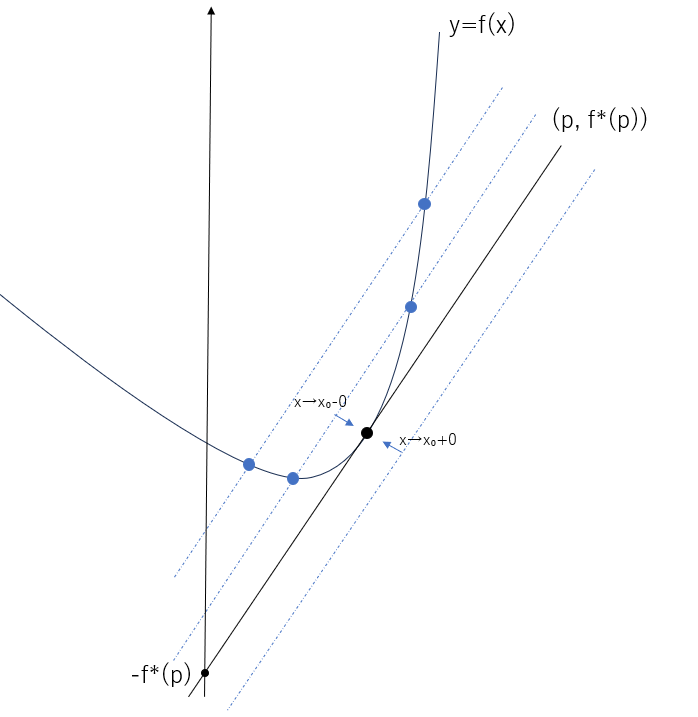
これとは対照的に $x$ に着目した表現をするのなら
$$f^*(p)=\max_x(px-f(x))\tag{7}$$
となる。 $px-f(x)$ が大きくなると(5)式の線座標系で表現している $y$ 切片 $-f^*(p)$ が小さくなる。このとき2つの共有点の距離は小さくなりやがて接する。つまり(7)式で用いられる $f(x)$ 上の点 $x$ とは $p$ が傾きとなる接線の接点となるのだ。
ちょっと休憩
本記事ではルジャンドル変換という言葉を出さずに暗にルジャンドル変換の定義へ誘導している。初学者にとってルジャンドル変換は慣れない概念の1つである。次回ではルジャンドル変換の定義に入るが本記事を読んでくれた読者ならすんなりと受け入れられるはずだろう。
次回


コメント