初めに
高校数学で習ったように階乗とは自然数 $n$ に対して、$n!=n(n−1)(n−2)⋯2⋅1$ と表されるものです。しかしこの定義では非自然数の場合には使えません。そこで非自然数の階乗を定義するために、ガンマ関数が用いられます。
ガンマ関数とは以下の性質
$$Γ(n+1)=nΓ(n)$$
を持っています。この性質を用いると、正の整数 $n$ に対して、
$$\begin{align*}
Γ(n+1)
&=nΓ(n)=n(n-1)Γ(n-1)\\
&=n(n-1)(n-2)\cdot\cdots\cdot k\cdot Γ(k)\\
&=n!
\end{align*}$$
となります(ただし $0<k≤1$ )。つまりこのように正の整数 $n$ に対して階乗と一致するような関数がガンマ関数として定義されているのです(本来は対数的に凸だとかいう条件が必要なのですが、ここでは厳密さよりも直感的に理解しやすく書きます)。殆どのサイトではこの $n$ が正の整数以外にも成り立つように定義が可能である理由が書かれていません。そこで本記事ではガンマ関数の性質を満たす幾つかの定義を自然な形で導出していきます。
階乗 $n!$ の定義の拡張
自然数における階乗 $n!$ の別の定義
自然数を $n$ と置くと、 $n$ の階乗とは
$$n!:=n(n-1)(n-2)\cdot\cdots\cdot 2\cdot 1$$
と表されるのだった。例えば $4!=4\cdot 3\cdot 2\cdot 1=24$ となる。
まずはこの階乗を何か関数で表してみよう。
理系の学生なら高校時代に何度も計算させられたことだろう
$$f(x)=\dfrac{1}{x}$$
の $n$ 次導関数 $f(x)^{(n)}$ である。 この関数の$n$ 次導関数 $f(x)^{(n)}$ は
$$f(x)^{(n)}=\dfrac{(-1)^nn!}{x^{n+1}}$$
となる。ここで左辺の微分形式を変更し
$$\begin{align*}
\left(\dfrac{d}{dx}\right)^n\dfrac{1}{x}&=\dfrac{(-1)^nn!}{x^{n+1}}\\
∴ \left(-\dfrac{d}{dx}\right)^n\dfrac{1}{x}&=\dfrac{n!}{x^{n+1}}
\end{align*}$$
とする。これにより階乗 $n!$ は
$$n!:=\left(-\dfrac{d}{dα}\right)^n\left.\dfrac{1}{α}\right|_{α=1} \tag{1}$$
と再定義することができよう。
正の実数における階乗 $x!$ への拡張
しかしこの定義は単に $n$ が自然数のときの階乗を再定義したものであり、これでは非自然数のときには使えないのだ。
そこで $\dfrac{1}{α}$ を $C^∞$ 級関数の何かで表現するために
$$\dfrac{1}{α}=\int_0^{∞}e^{-αt}dt \tag{2}$$
と広義積分を用いて置くことにしよう。ただし $α>0$ としている。ここでなぜ考える関数を $C^∞$ 級関数にしたのかといえば、後に分かるが単純に自然数 $n$ がどんなに大きい値を取っても良いようにするためである。
よって階乗 $n!$ は(1)、(2)式より
$$\begin{align*}
n!
&:=\left(-\dfrac{d}{dα}\right)^n\left.\dfrac{1}{α}\right|_{α=1}\\
&=\left(-\dfrac{d}{dα}\right)^n\left.\int_0^{∞}e^{-αt}dt\right|_{α=1}
\end{align*} \tag{3}$$
となる。更に $e^{-at}$ は $C^∞$ 級関数であるから微分と積分の順序を交換することができ
$$\begin{align*}
n!
&=\left(-\dfrac{d}{dα}\right)^n\left.\int_0^{∞}e^{-αt}dt\right|_{α=1}\\
&=\left.\int_0^{∞}\left(-\dfrac{∂}{∂α}\right)^ne^{-αt}\right|_{α=1}dt\\
&=\left.\int_0^{∞}t^ne^{-αt}\right|_{α=1}dt\\
&=\int_0^{∞}t^ne^{-t}dt
\end{align*} \tag{4}$$
となる。
この右辺を $Π(n)$ と置くと、開区間 $(-1,∞)$ の範囲で
$$Π(n)=\int_0^{∞}t^ne^{-t}dt$$
は連続である。よってこの区間において非整数となる $n$ の階乗 $n!$ を関数 $Π(n)$ を用いて
$$n!:=Π(n) \tag{5}$$
と定義することができるのだ。この $Π$ 関数は当然ながら任意の正の実数において階乗の基本的な性質
$$\begin{align*}
Π(n)
&=nΠ(n-1)=n(n-1)Π(n-2)\\
&=n(n-1)(n-2)\cdot\cdots\cdot (k+1)\cdot Π(k)\\
&=n!
\end{align*} \tag{6}$$
を持っている。ただし $0<k≤1$ とした。
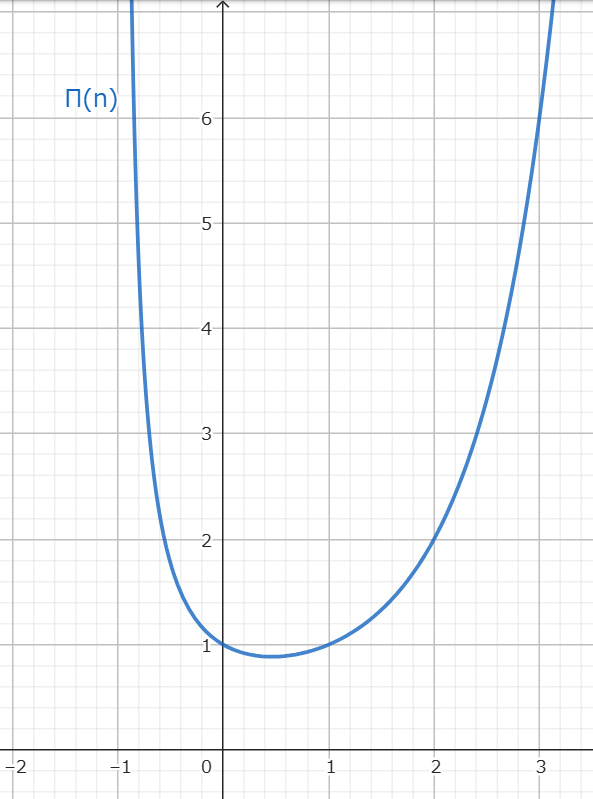
ガウスはこのように $Π$ を用いて表記したが、ルシャンドルは $Γ$ を用いて
$$\begin{align*}
Γ(n+1)
&=nΓ(n)=Π(n)\\
&=\int_0^{∞}t^{n}e^{-t}dt
\end{align*}$$
のように表記した。なおサラっと流したがガンマ関数は $Π$ 関数を $n$ 方向に $1$ だけ平行移動させたものなので、(6)式同様の階乗の基本的な性質
$$\begin{align*}
Γ(n+1)
&=nΓ(n)=n(n-1)Γ(n-1)\\
&=n(n-1)(n-2)\cdot\cdots\cdot k\cdot Γ(k)\\
&=n!
\end{align*} \tag{7}$$
が成り立つ。ただし $0<k≤1$ とした。
ルシャンドルの $Γ$ 表現は $x$ を開区間 $(0,∞)$ に限定する。つまり任意の正の実数における階乗 $x!$ を
$$x!=Γ(x+1)$$
のように表現することで、ガンマ関数 $Γ(x)$ は正の実数 $x$ の範囲にのみ値域を存在させることができるのである。よって数学や物理学の分野ではこのガンマ関数が利用されることが殆どである。
負の実数における階乗 $x!$ への拡張
なおガンマ関数は(7)式を用いて
$$\begin{align*}
Γ(x+n+1)&=x(x+1)(x+2)\cdot\cdots\cdot (x+n)\cdot Γ(x) \tag{7}
\\
Γ(x)&=\dfrac{Γ(x+n+1)}{x(x+1)(x+2)\cdot\cdots\cdot (x+n)}
\end{align*}\tag{8}$$
と表現することができる。(8)式を用いることで $x$ が負の値を取るときにも $x!$ を定義することが可能なのだ。一応ボーア・モレルップの定理
関数 $f(x)$ が以下の1~3をすべて満たすならば, その定義域において $f(x)$ はガンマ関数と一致する。
ボーア・モレルップの定理
- $f(x + 1)=xf(x)$
- $f(x)$ の定義域は $x>0$ を含み、そこでは対数的凸である
- $f(1)=1$
を用いることでガンマ関数を別の方法で定義することもできる。こちらの定義で導出するガンマ関数は負の数にも拡張されるので、簡単に導出してみる。
まず条件2.の対数的凸であるということは以下の不等式が成り立つ。
$$\dfrac{\log f(−1+n)−\log f(n)}{(−1+n)−n}
≤\dfrac{\log f(x+n)−\log f(n)}{(x+n)−n}
≤\dfrac{\log f(1+n)−\log f(n)}{(1+n)−n} \tag{9}$$
ただし $n$ を $n≥2$ の整数とし、 $x$ を $0<x≤1$ とする。よって(9)式は条件1.より
$$\begin{cases}
f(-1+n)=(n-2)!\\
f(n)=(n-1)!\\
f(1+n)=n!\\
Γ(x+n)=x(x+1)(x+2)\cdot\cdots\cdot (x+n-1)\cdot Γ(x) \tag{7}
\end{cases}$$
を代入すると、
$$\begin{align*}
\log(n−1)≤\dfrac{\log f(x+n)−\log(n−1)!}{x}≤\log n\\
∴\log{(n−1)^x(n−1)!}≤\log f(x+n)≤\log{n^x(n − 1)!}
\end{align*}\tag{10}$$
ここで
$$\begin{cases}
(n-1)^x>0\\
(n-1)!>0\\
n>0
\end{cases}$$
であるから(10)式の各辺の $\log$ を取って
$$\begin{align*}
(n−1)^x(n−1)!&≤f(x+n)≤n^x(n − 1)!\\
∴ \dfrac{(n−1)^x(n−1)!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n-1)}&≤f(x)≤\dfrac{n^x(n − 1)!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n-1)}
\end{align*}\tag{11}$$
となる。ここで $n→∞$ の極限を取ると(11)式の両側は
$$\begin{align*}
&\lim_{n→∞}\dfrac{(n−1)^x(n−1)!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n-1)}\\
=&\lim_{n→∞}\dfrac{n^xn!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n)}\\
\end{align*}$$
$$\begin{align*}
&\lim_{n→∞}\dfrac{n^x(n−1)!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n-1)}\\
=&\lim_{n→∞}\dfrac{n^xn!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n)}
\end{align*}$$
となる。よって(11)式は
$$\begin{align*}
\lim_{n→∞}\dfrac{n^xn!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n)}&≤f(x)≤\lim_{n→∞}\dfrac{n^x(n − 1)!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n-1)}
\end{align*}\tag{12}$$
となる。(12)式は両側を同じ極限で挟んでいるので、挟み撃ちの原理から
$$f(x)=\lim_{n→∞}\dfrac{n^xn!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n)}\tag{13}$$
となる。また(12)式は $x<0$ についても成り立つので、(13)式はボーア・モレルップの定理から、任意の実数において極限値が存在するのである。ただしここで条件1. $f(x + 1)=xf(x)$ $f(x)$ より $0$ を含む負の整数以外では極限値が存在しないことに注意されたい。
そこで
$$Γ_n(x)=\dfrac{n^xn!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n)}$$
と置くと
$$\begin{align*}
Γ_n(x + 1)
&=xΓ_n(x)\dfrac{n}{x+n+1}\\
Γ_n(x)
&=\dfrac{1}{x}\dfrac{x+n+1}{n}
Γ_n(x + 1)
\end{align*}\tag{14}$$
が成り立つ。
(14)式によると $\displaystyle\lim_{n→∞}Γ_n(x)$ が収束すると $\displaystyle\lim_{n→∞}Γ_n(x+1)$ が収束し、 $\displaystyle\lim_{n→∞}Γ_n(x)$ が収束すると $\displaystyle\lim_{n→∞}Γ_n(x)$ は収束するのだ。よって $0<x≤1$ の範囲では $Γ(x)=\displaystyle\lim_{n→∞}Γ_n(x)$ が存在することは既に示されているので $0$ を除く任意の正の値の範囲で $Γ(x)$ の極限は収束する。更に言えば負の値の範囲については非整数のみ $Γ(x)$ の極限は収束するのだ。
よって $0$ と負の整数を除く任意の実数の範囲で $Γ(x)$ は収束することが言え、先の条件1. $f(x + 1)=xf(x)$ により $Γ(x)$ を任意の実数の範囲で定義することができるのである。
よって一般に $x$ を任意の実数に拡張した場合には
$$Γ(x)=\lim_{n→∞}\dfrac{n^xn!}{x(x+1)(x+2)\cdot\cdots\cdot (x+n)}\tag{15}$$
となる。
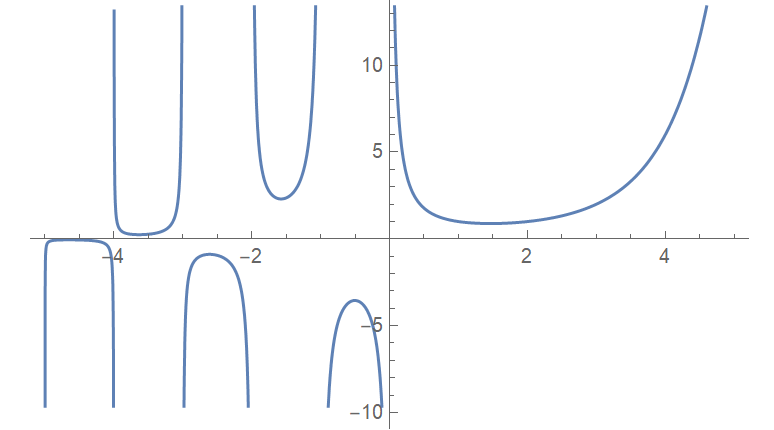
$x$ が負の整数、0の場合には発散する
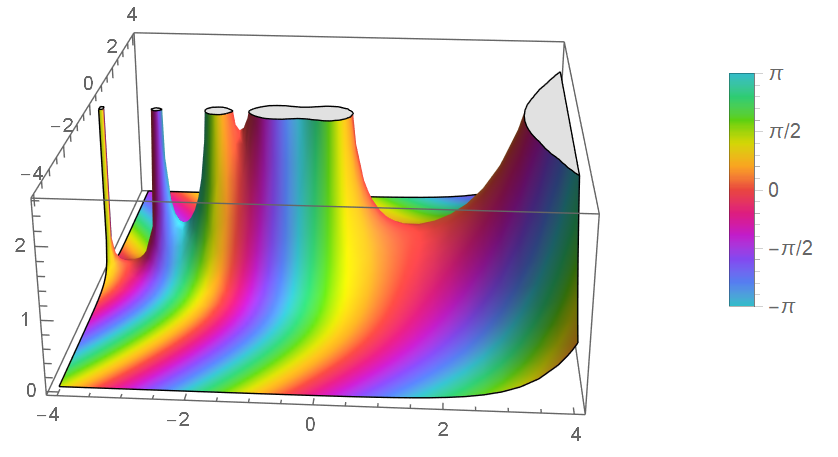
図はガンマ関数 $\Gamma(z)$ の絶対値となる
ガンマ関数の実用例
ここではガンマ関数を用いることで考え方に幅を広げられる例を挙げていこう。
非整数階の微分
$n$ 次の整数の多項式で表される関数
$$\begin{align*}
f(x)
&=a_0+a_1x^1+\cdots +a_nx^n\\
&=\sum_{j=0}^na_jx^j
\end{align*}$$
を $k(≤n)$ 回微分すると
$$\begin{align*}
f(x)^{(k)}
&=a_k\binom{k}{k}k!+a_{k+1}\binom{k+1}{k}k!x^1+\cdots +a_n\binom{n}{k}k!x^{n-k}\\
&=a_kk!+a_{k+1}\dfrac{(k+1)!k!}{k!1!}x^1+\cdots +a_n\dfrac{n!k!}{k!(n-k)!}x^{n-k}\\
&=a_kk!+a_{k+1}\dfrac{(k+1)!}{1!}x+\cdots +a_n\dfrac{n!}{(n-k)!}x^{n-k}\\
&=\sum_{j=k}^{n}a_j\dfrac{j!}{(j-k)!}x^{j-k}
\end{align*}\tag{16}$$
となる。
途中の $\displaystyle\binom{n}{r}$ は二項係数であり、
$$\binom{n}{r}= {}_n\mathrm{C}_r=\dfrac{n!}{r!(n-r)!}$$
である。よって $n!=Γ(n+1)$ を代入すると(16)式は
$$\begin{align*}
f(x)^{(k)}
&=\sum_{j=k}^{n}a_j\dfrac{Γ(j+1)}{Γ(j-k+1)}x^{j-k}
\end{align*}\tag{17}$$
とガンマ関数を用いて表現される。これにより正の整数以外にも $n$ 階導関数を定義することが可能である。例えば $x^2$ の $\frac{1}{2}$ 階導関数は
$$\begin{align*}
\dfrac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}x^2
&=\dfrac{Γ(2+1)}{Γ(\frac{3}{2}+1)}x^{{\frac{3}{2}}}\\
&=\dfrac{2!}{\dfrac{1}{2}Γ(\frac{1}{2})}x^{{\frac{3}{2}}}\\
&=4x\sqrt{\dfrac{x}{π}}
\end{align*}$$
となる。因みにもう一度 $\frac{1}{2}$ 階導関数を求めると
$$\begin{align*}
\dfrac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}\left(\dfrac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}x^2\right)
&=\dfrac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}\left(\dfrac{Γ(2+1)}{Γ(\frac{3}{2}+1)}x^{{\frac{3}{2}}}\right)\\
&=\dfrac{Γ(2+1)}{Γ(\frac{3}{2}+1)}\dfrac{Γ(\frac{3}{2}+1)}{Γ(1+1)}x^1\\
&=2x
\end{align*}$$
となり $1$ 階導関数と一致する。
非整数乗の展開
二項定理によれば $n$ 次式は
$$(x+y)^n=\sum_{k=0}^n\binom{n}{k}x^{n-k}y^k$$
のように展開することができる。ここで $n$ は自然数とされているが、ガンマ関数を用いれば $n$ を実数に拡張することが可能である。例えば
$$\dfrac{1}{\sqrt{1-x^2}}$$
は
$$\begin{align*}
\dfrac{1}{\sqrt{1-x^2}}
&=\binom{-\frac{1}{2}}{0}+\binom{-\frac{1}{2}}{1}(-x^2)+\binom{-\frac{1}{2}}{2}(-x^2)^2+\cdots\\
&=\dfrac{Γ(-\frac{1}{2}+1)}{Γ(1)Γ(-\frac{1}{2}+1)}+\dfrac{Γ(-\frac{1}{2}+1)}{Γ(1+1)Γ(-\frac{1}{2})}(-x^2)+\dfrac{Γ(-\frac{1}{2}+1)}{Γ(2+1)Γ(-\frac{1}{2}-1)}(-x^2)^2+\cdots\\
&=\dfrac{1}{Γ(1)}+\dfrac{-\frac{1}{2}Γ(-\frac{1}{2})}{Γ(1+1)Γ(-\frac{1}{2})}(-x^2)+\dfrac{-\frac{1}{2}\cdot(-\frac{3}{2})Γ(-\frac{1}{2}-1)}{Γ(2+1)Γ(-\frac{1}{2}-1)}(-x^2)^2+\cdots\\
&=1+\dfrac{1}{2}x^2-\dfrac{1\cdot 3}{2\cdot 2}\dfrac{1}{2!}(x^2)^2+\dfrac{1\cdot 3\cdot 5}{2\cdot 2\cdot 2}\dfrac{1}{3!}(x^2)^3-\cdots\\
&=1+\dfrac{1}{2}x^2+\dfrac{1\cdot 3}{2\cdot 4}x^4+\dfrac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}x^6+\cdots
\end{align*}$$
のように整級数展開することができる。この積分
$$\int_0^x\dfrac{1}{\sqrt{1-x^2}}$$
は各項を積分すれば良く、
$$\begin{align*}
\int_0^x\dfrac{1}{\sqrt{1-x^2}}
&=x+\dfrac{1}{2}\dfrac{x^3}{3}+\dfrac{1\cdot 3}{2\cdot 4}\dfrac{x^5}{5}+\dfrac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\dfrac{x^7}{7}+\cdots
\end{align*}$$
となり、これは逆三角関数 $\text{arcsin}\hspace{1mm}x$ と一致する。
この例ではマクローリン展開を用いて逆三角関数を求めた方が簡単だが、二項定理の方は微分をしないで済む。そのため $x$ が複雑な関数で表される場合には、こちらの方が煩雑な計算を避けることができよう。
逆三角関数についてはこちらの記事を参照されたい。
最後に
本記事ではガンマ関数の定義を高校数学で習った階乗 $n!$ の定義から自然に導出してみた。本記事ではガンマ関数を実数で定義したが実は複素数でも定義できるそうである。しかし本サイトではあまり実用的ではないため実数にのみ限定した。



コメント