初めに
本記事は4部構成のシリーズ「極座標系でも運動方程式を解きたい」の第2部になっています。このシリーズでは周期的な平面運動について紹介していきます。第2部では第1部での動機付けを元に向心力のみが働く運動について解説していきます。向心力のみが働く場合には以下の4つの運動
- 円運動
- 楕円
- 放物線
- 双曲線
のいずれかとなります。これは力学的エネルギーの大きさによって決まります。このように運動を区別するときには一般に有効ポテンシャル $U_{eff}$ を用いられることが多いので、本記事でも簡単に紹介していこうと思います。
初回(前回)
次回
一般に向心力のみが働く場合
エネルギー保存則を解析する
円座標系の運動方程式(7)式
$$m
\begin{pmatrix}
\ddot{r} -r\dot{θ}^2 & 2\dot{r}\dot{θ}+r\ddot{θ}
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{r_{(θ)}}\\
\boldsymbol{e}_{θ_{(θ)}}
\end{pmatrix}=
\begin{pmatrix}
F_r & F_θ
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{r_{(θ)}}\\
\boldsymbol{e}_{θ_{(θ)}}
\end{pmatrix} \tag{7}$$
の法線方向 $\boldsymbol{e}_{θ_{(θ)}}$ をもう少し変形すると
$$2\dot{r}\dot{θ}+r\ddot{θ}=\frac{1}{r} \frac{d}{dt}\left(r^2\dot{θ}\right) \tag{10}$$
となるから、(7)式は(10)式によって
$$\begin{align*}
(7)&=m
\begin{pmatrix}
\ddot{r} -r\dot{θ}^2 & \dfrac{1}{r} \dfrac{d}{dt}\left(r^2\dot{θ}\right)
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{r_{(θ)}}\\
\boldsymbol{e}_{θ_{(θ)}}
\end{pmatrix}\\
&=
\begin{pmatrix}
F_r & F_θ
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{r_{(θ)}}\\
\boldsymbol{e}_{θ_{(θ)}}
\end{pmatrix}
\end{align*} \tag{7亜}$$
と書き表される。(7)式の亜式といったところか。これで準備完了である。
物体に向心力のみが働いている場合とは、言い換えれば法線方向 $\boldsymbol{e}_{θ_{(θ)}}$ の力 $F_θ=0$ となるということである。よって
$$\begin{align*}
\frac{1}{r} \frac{d}{dt}\left(r^2\dot{θ}\right)&=0\\
∴ \dot{θ}&=C\frac{1}{r^2} (Cは任意定数)
\end{align*} \tag{11}$$
また円座標系において速度 $v$ が
$$\boldsymbol{v}=\dot{r}\boldsymbol{e}_{r_{(θ)}}+r\dot{θ}\boldsymbol{e}_{θ_{(θ)}}$$
と表されることから、向心力のみが働くときのエネルギー保存則は
$$\begin{align*}
\frac{1}{2} m|\boldsymbol{v}|^2+U_{(\boldsymbol{r})}&=E_{(\boldsymbol{r})}\\
∴ \frac{1}{2} m(\dot{r}^2+r^2\dot{θ}^2)+\frac{α}{r}&=E_{(r,θ)}
\end{align*} \tag{12}$$
のように表される($E_{(\boldsymbol{r})}$ は力学的エネルギー)。ただし $\frac{α}{r}$ は向心力のポテンシャルとした。運動方程式(7)式の半径方向 $\boldsymbol{e}_{r_{(θ)}}$ からも求められるが、向心力のポテンシャルとエネルギーの関係が分かるエネルギー保存則を利用すると色々と便利である。というのも後で求める解の形を見ればわかるが、有効ポテンシャル
$$U_{eff}=\frac{1}{2}mr^2\dot{θ}^2+\frac{α}{r}$$
という、本来はポテンシャルではないものでもポテンシャルと同等に扱えそうだという期待を秘めて、これらをポテンシャルと見なしたもの、の大きさによって物体の軌道を判定することもできるのだ。
有効ポテンシャル $U_{eff}$ と4つの軌道
右図には有効ポテンシャル $U_{eff}$ のグラフを表した。ここで力学的エネルギー $E_{(\boldsymbol{r})}$ を運動エネルギー $K_{(\boldsymbol{r})}$ と有効ポテンシャル $+U_{eff(\boldsymbol{r})}$ を用いて
$$E_{(\boldsymbol{r})}=K_{(\boldsymbol{r})}+U_{eff(\boldsymbol{r})}$$
と置く。また $\boldsymbol{r}=\boldsymbol{c}$ となるときに速度 $\dot{r}=0$ となるとする。つまり点 $\boldsymbol{c}$ とは速度
$$\boldsymbol{v}=\dot{r}\boldsymbol{e}_{r_{(θ)}}+r\dot{θ}\boldsymbol{e}_{θ_{(θ)}}$$
の半径方向の成分 $\dot{r}\boldsymbol{e}_{r_{(θ)}}$ が無いような点のことである。
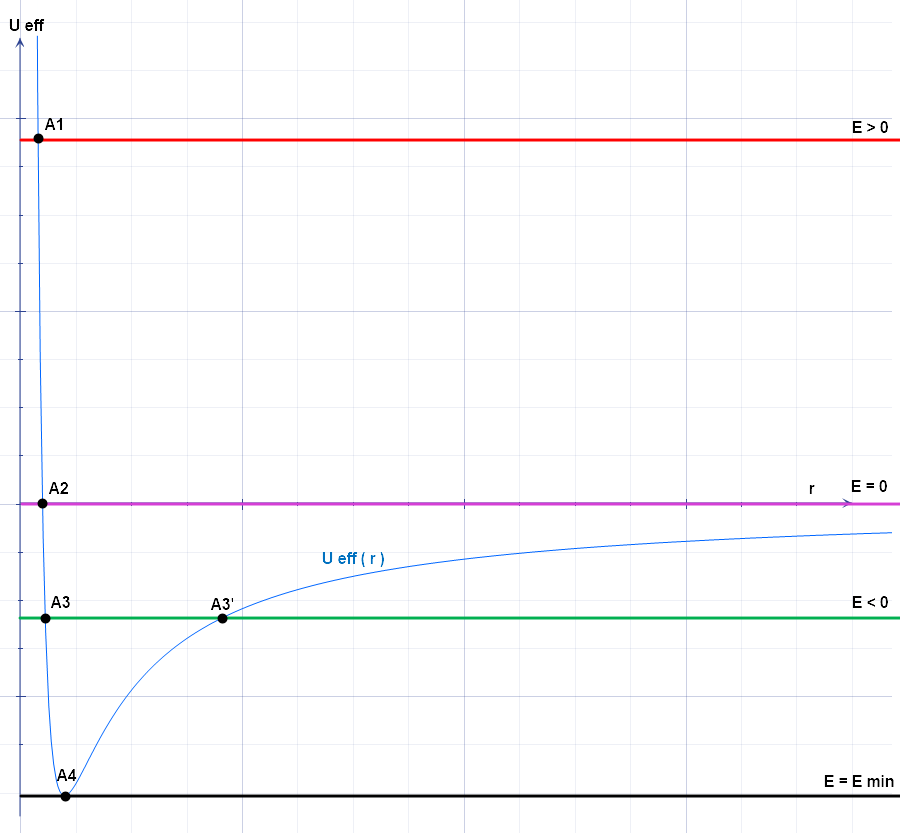
$E>0$; 双曲線軌道
$E=0$; 放物線軌道
$E<0$; 楕円軌道
$E=E_{min}$; 円軌道
出典:Wiki
この点においては運動エネルギー $K_{(\boldsymbol{r})}=0$ であるから、エネルギー保存則は
$$E_{(\boldsymbol{r})}=E_{(\boldsymbol{c})}=U_{eff(\boldsymbol{c})}$$
となる。点 $\boldsymbol{c}$ とは有効ポテンシャルのグラフで言えば力学的エネルギー $E_{(\boldsymbol{r})}$ と有効ポテンシャル $U_{eff(\boldsymbol{r})}$ が交わる点である $A_n$ である。
よって有効ポテンシャルのグラフを見れば分かる通り、 $E_{(\boldsymbol{r})}<0$ となるときには物体は周期運動をし、力学的エネルギーとの交点 $A_n$ においては半径方向の速度成分は0となるのだ。
エネルギー保存則からの解の導出
よって(11)式をエネルギー保存則(12)式に代入すると
$$\frac{1}{2} m(\dot{r}^2+r^2\left(C\frac{1}{r^2}\right)^2)+\frac{α}{r}=E \tag{13}$$
となる。ここで $\dot{r}$ について $θ$ で挟んで合成関数の微分を利用すると
$$\dot{r}=\frac{dr}{dt}=\frac{dθ}{dt} \frac{dr}{dθ}$$
が得られ、再度(11)式を代入して
$$\dot{r}=C\frac{1}{r^2} \frac{dr}{dθ}$$
となる。よって(13)式は
$$\frac{1}{2} m\left(\left(C\frac{1}{r^2} \frac{dr}{dθ}\right)^2+r^2\left(C\frac{1}{r^2}\right)^2\right)+\frac{α}{r}=E \tag{14}$$
となる。しかしこのままではよく分からないので、取り敢えず $\frac{1}{r}$ を上手い具合に消去したい。そこで
$$u=\frac{1}{r}⇒\frac{du}{dr}=-\frac{1}{r^2}$$
と置いてみると、
$$\frac{dr}{dθ}=\frac{du}{dθ}\frac{dr}{du}$$
より(14)式は
$$\begin{align*}
\frac{1}{2} m\left(\left(C\frac{1}{r^2} \frac{du}{dθ} r^2\right)^2+\frac{1}{u^2}\left(Cu^2\right)^2\right)+αu&=E\\
∴ \frac{1}{2} m\left(\left(C\frac{du}{dθ}\right)^2+C^2u^2\right)+αu&=E\\
∴ \left(\frac{du}{dθ}\right)^2+u^2+\frac{2α}{C^2m}u&=\frac{2E}{C^2m}\\
∴ \left(\frac{du}{dθ}\right)^2+\left(u+\frac{α}{C^2m}\right)^2-\left(\frac{α}{C^2m}\right)^2&=\frac{2E}{C^2m}\\
∴ \left(\frac{du}{dθ}\right)^2+\left(u+\frac{α}{C^2m}\right)^2&=\left(\frac{α}{C^2m}\right)^2+\frac{2E}{C^2m}
\end{align*} \tag{15a}$$
となり $r$ の代わりに $u$ を用いることで簡潔に表される 。ここで(15a)式を
$$∴ \left(\frac{du}{dθ}\right)^2+(u+A)^2=B^2 \tag{15b}$$
のように
$$\begin{cases}
A=\dfrac{α}{C^2m}\\
B^2=A^2+\dfrac{2E}{C^2m}
\end{cases}$$
で置いてあげれば、(15a,b)式を満たす $u$ を定めやすくなる。多分読者の方も薄々感じていることだろう。分からない人のためにより分かりやすい例として
$$x^2+y^2=B^2 \tag{16}$$
を考えようと思う。が、(16)式は考えるまでもなく
$$\begin{cases}
x=B\cos(θ+δ)\\
y=B\sin(θ+δ)
\end{cases}$$
であることが分かる( $δ$ は初期位相)。よって一見すると1階非線形非斉次微分方程式である(15b)式は、実は単純に
$$u_{(θ)}=B\cos(θ+δ)-A \tag{17}$$
のように解くことができる( $δ$ は初期位相)。よって求める $r$ は
$$r=\frac{1}{B\cos(θ+δ)-A}=\frac{-\dfrac{1}{A}}{1-\dfrac{B}{A}\cos(θ+δ)}=\frac{λ}{1+e\cos(θ+δ)} \tag{18}$$
となる( $λ=-\frac{1}{A},ε=-\frac{B}{A}$ )。(18)式は正に円座標系における2次曲線の方程式を表す。離心率 $e$ は具体的に
$$e^2=\frac{B^2}{A^2}=1+\frac{2C^2mE}{α^2} \tag{19}$$
となるから、任意定数 $C$ が定まれば(19)式から円、楕円、放物線、双曲線の場合のエネルギー $E$ を推定することができる。ここで求めた離心率 $e$ によって軌道の分類ができるが、この分類は有効ポテンシャル $U_{eff}$ での分類と等しくなる。
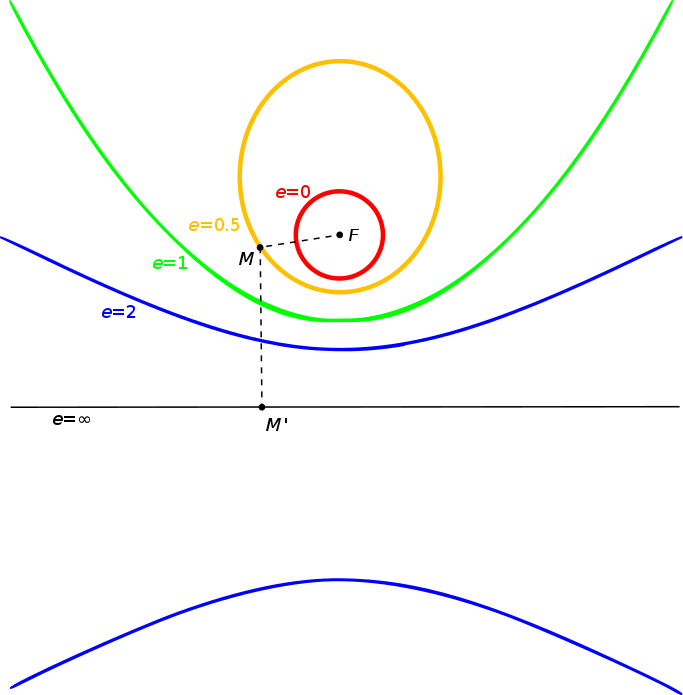
$e=0$; 円(赤)
$0<e<1$; 楕円(橙)
$e=1$; 放物線(緑)
$e>1$; 双曲線(青)
出典:Wiki
殆どのサイトではこの任意定数 $C$ を角運動量
$$\boldsymbol{L}=\boldsymbol{r}×\boldsymbol{p}=\boldsymbol{r}×m\boldsymbol{v}$$
$$∴l\boldsymbol{e}_z=mr^2\dot{θ}(\boldsymbol{e}_x×\boldsymbol{e}_y)=mr^2\dot{θ}\boldsymbol{e}_z$$
が保存することを用いて話を展開しているが、これは結局物体に向心力のみが働く場合の法線方向の解(11)式
$$∴ \dot{θ}=C\frac{1}{r^2} (Cは任意定数) \tag{11}$$
の任意定数 $C$ をわざわざ置き換えてているだけにすぎない。
ちょっと休憩
本記事では円座標系について向心力のみが働くときを解説してきた。次回以降は向心力以外に外力が働く場合や球座標系の運動方程式についても触れるつもりである。本記事では角運動量保存則を用いていないが、代わりに向心力以外が働いていない(つまり接線方向に力が働いていない)ときの運動方程式を利用した。角運動量についてはいずれ紹介するので、それまで我慢させることになってしまうことを許してほしい。
初回(前回)
次回



コメント