初めに
この記事は4部構成のシリーズ「極座標系でも運動方程式を解きたい」の第3部になっています。このシリーズでは周期的な平面運動について紹介していきます。第3部では向心力以外に外力が働く物体の運動を見ていこうと思います。ここでは単振り子の運動の厳密解を調べます。
式番号は引き継ぎ。
初回
前回
次回
円運動の向こう側へ
単振り子
円運動のときには制約条件 $x^2+y^2=r^2=Const.$ が課されるのであった。円運動における微分方程式(8)式をもう一度書く。
$$m
\begin{pmatrix}
-r\dot{θ}^2 & r\ddot{θ}
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{r_{(θ)}}\\
\boldsymbol{e}_{θ_{(θ)}}
\end{pmatrix}=
\begin{pmatrix}
F_r & F_θ
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{r_{(θ)}}\\
\boldsymbol{e}_{θ_{(θ)}}
\end{pmatrix} \tag{8}$$
右図のような単振り子をする物体について考える。右図の物体には半径方向内向きに張力 $\boldsymbol{S}$ が働き、 $x$ 軸正の向き(↓向き)に重力 $\boldsymbol{mg}$ が働く。よって物体に働く力 $\boldsymbol{F}$ を円座標系で表示すると
$$\boldsymbol{F}=-S\boldsymbol{e}_r+mg\boldsymbol{e}_x=-S\boldsymbol{e}_r+mg\cosθ\boldsymbol{e}_r-mg\sinθ\boldsymbol{e}_θ$$
となる。なおサラっと流したが、基底は直交していることから極座標系の基底を $\langle\boldsymbol{e}_{r_{θ}}=(\cosθ,\sinθ),\boldsymbol{e}_{θ_{θ}}=(-\sinθ,\cosθ)\rangle$ として
$$\boldsymbol{e}_y=(\boldsymbol{e}_y\cdot\boldsymbol{e}_r)\boldsymbol{e}_r+(\boldsymbol{e}_y\cdot\boldsymbol{e}_θ)\boldsymbol{e}_θ$$
を満たすことを利用した(勿論図形的に見ても良い)。
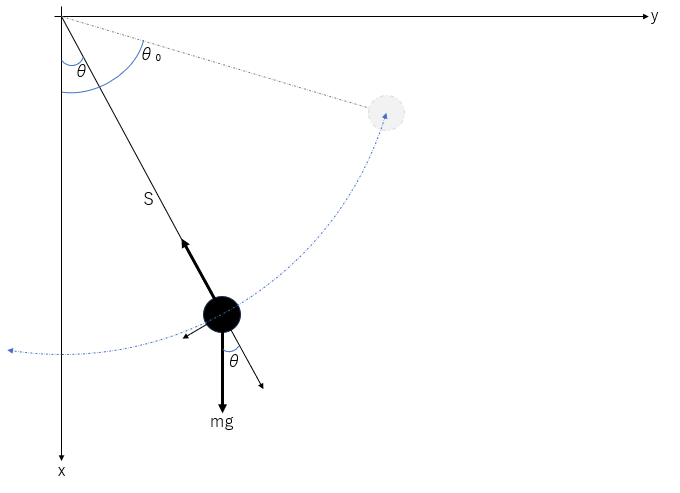
鉛直下向き↓が $x$ 軸正の向き、水平右向き→が $y$ 軸正の向き
よって単振り子の腕の長さを $l$ と置くと運動方程式(8)式は
$$m
\begin{pmatrix}
-l\dot{θ}^2 & l\ddot{θ}
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{r_{(θ)}}\\
\boldsymbol{e}_{θ_{(θ)}}
\end{pmatrix}=
\begin{pmatrix}
S-mg\cosθ & -mg\sinθ
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{e}_{r_{(θ)}}\\
\boldsymbol{e}_{θ_{(θ)}}
\end{pmatrix} \tag{20}$$
となる。よって(20)式を連立微分方程式と見なして $θ,S$ を求めることができそうである。そこでまず接線 $\boldsymbol{e}_θ$ 方向の運動方程式
$$\begin{align*}
ml\ddot{θ}&=-mg\sinθ\\
∴\ddot{θ}&=-\frac{g}{l}\sinθ\\
∴\ddot{θ}&=-ω^2\sinθ
\end{align*} \tag{21}$$
を解いてみようと思う( $ω=\sqrt{\frac{g}{l}}(≥0)$ と置いた)。ここで特別に $\dot{θ}_{(t)}=Φ$ と置き(21)式の左辺を
$$\dot{Φ}=\frac{dθ}{dt}\frac{dΦ}{dθ}=Φ\frac{dΦ}{dθ}$$
のように変形すれば、(21)式は
$$Φ\frac{dΦ}{dθ}=-ω^2\sinθ$$
となる。後はこれの両辺を $θ$ で積分すれば良い。左辺は合成関数の積分で、
$$\begin{align*}
∫Φ\frac{dΦ}{dθ} dθ&=Φ^2-∫\frac{dΦ}{dθ} Φdθ\\
∴ ∫Φ\frac{dΦ}{dθ} dθ&=\frac{1}{2} Φ^2
\end{align*}$$
となるから、
$$\begin{align*}∴ \frac{1}{2} Φ^2&=ω^2\cosθ+A (Aは任意定数)\\
∴Φ_{({θ_{(t)}})}=\dot{θ}_{(t)}&=±\sqrt{2(ω^2\cosθ+A)}
\end{align*} \tag{22}$$
となり、更にこれを $t$ で積分すれば(左辺は $θ$ で置換)
$$∴ \displaystyle∫\frac{dθ}{\sqrt{2(ω^2\cosθ+A)}}=±∫dt$$
が得られる……🙃。右辺は周期となるが、左辺がよく分からない。そこで三角関数の加法定理 $\cosθ=1-2\sin^2\left(\frac{θ}{2}\right)$ から左辺を
$$\displaystyle∫\frac{dθ}{\sqrt{2(ω^2+A)-4ω^2\sin^2\left(\frac{θ}{2}\right))}}=\displaystyle∫\frac{dθ}{2ω\sqrt{k^2-\sin^2\left(\frac{θ}{2}\right)}} \tag{23}$$
のように変形してみる。ただし $k^2=\frac{1}{ω^2} (ω^2+A)$ と置いた。よって
$$\sin\left(\frac{θ}{2}\right)=kz⇒kdz=\frac{1}{2} \cos\left(\frac{θ}{2}\right)dθ=\frac{1}{2} \sqrt{1-\sin^2\left(\frac{θ}{2}\right)}dθ=\frac{1}{2}\sqrt{1-k^2z^2}dθ$$
と置換する(簡単のため $(0≤θ≤π/2)⇒(kz≥0)$ の範囲で議論している)と(23)式は
$$\begin{align*}
(23)&=\displaystyle∫\frac{kdz}{ω\sqrt{(k^2-k^2z^2)(1-k^2z^2)}}\\
&=\displaystyle∫\frac{dz}{ω\sqrt{(1-z^2)(1-k^2z^2)}}
\end{align*} \tag{24}$$
と変形できる($k≥0$ とした(理由は後述で明らかになる))。更に $z=\sinφ⇒dz=\cosφdφ$ と置くと(24)式は
$$\begin{align*}
(24)&=\displaystyle∫\frac{\cosφdφ}{ω\sqrt{(1-\sin^2φ)(1-k^2\sin^2φ)}}\\
&=\displaystyle∫\frac{dφ}{ω\sqrt{1-k^2\sin^2φ}}
\end{align*} \tag{25}$$
となる。
さて任意定数 $A$ について、(22)式
$$∴Φ=\dot{θ}=±\sqrt{2(ω^2\cosθ+A)} \tag{22}$$
は $Φ_{({θ_{(0)}})}=\dot{θ}_{(0)}=0$ になる(つまり初速が $0$ である)ことから、
$$A=-ω^2\cosθ_{Max}$$
となる($θ_{Max}$ は物体の最高点における角度 $θ$ とした)。よって
$$\begin{align*}
k^2&=\frac{1}{ω^2} (ω^2+A)\\
&=\frac{1}{2ω^2} (ω^2-ω^2\cosθ_{Max})\\
&=\left(\frac{1-\cosθ_{Max}}{2}\right)\\
&=\sin^2\left(\frac{θ_{Max}}{2}\right)\\
∴ k&=\sin\left(\frac{θ_{Max}}{2}\right) (∵\sin\left(\frac{θ_{Max}}{2}\right)≥0)
\end{align*}$$
を得る。よって置換した積分範囲は以下のようになる。
| 変数 | 下端 | 周期 $T/4$ | 上端 |
|---|---|---|---|
| $θ$ | $0$ | $→$ | $θ_{Max}$ |
| $z=\frac{1}{k}\sin\left(\frac{θ}{2}\right)$ | $0$ | $→$ | $1$ |
| $φ=\text{Arcsin}\hspace{1mm} z$ | $0$ | $→$ | $\dfrac{π}{2}$ |
| $k=\sin\left(\frac{θ_{Max}}{2}\right)$ |
よって(22)式を解くためには積分
$$\displaystyle∫_0^{\small{\dfrac{π}{2}}}\frac{dφ}{\sqrt{1-k^2\sin^2φ}}$$
を実行することになる。このとき積分範囲 $[φ:0→\frac{π}{2}]$ は周期 $\frac{T}{4}$ にあたるから、求める周期 $T$ は
$$T=4\displaystyle∫_0^{\small{\dfrac{π}{2}}}\frac{dφ}{ω\sqrt{1-k^2\sin^2φ}} \tag{26}$$
となる。なぜ右辺をこのような形にしたのかといえば
楕円関数の積分(第一種完全楕円積分)
$$\displaystyle∫_0^{\small{\dfrac{π}{2}}}\frac{dθ}{\sqrt{1-k^2\sin^2θ}}$$
を利用したかったからである。よってこの楕円関数の積分を利用すれば周期
$$T=\frac{2π}{ω}\sum_{n=0}^∞\left(\frac{(2n-1)!!}{(2n)!!}\right)^2k^{2n} \tag{27}$$
を得る。特に $n=0$ のときには接線方向の運動方程式(21)式
$$\ddot{θ}=-ω^2\sinθ \tag{21}$$
の $\sinθ$ を $θ≈0$ の下でマクローリン展開により近似した亜式
$$\ddot{θ}=-ω^2θ \tag{21亜}$$
を解いたときの周期 $T=\frac{2π}{ω}$ となる。そのため高校物理などでよくある $θ≈0$ は厳密解(27)式からも妥当であることが伺える。
単振動の運動方程式を解く
先述にチラッと登場した
$$\ddot{θ}=-ω^2θ \tag{21亜}$$
は単振動を表す運動方程式である。これを解くには2階線型斉次微分方程式を解くことになるが、少し知識が必要である。ここでは1階線型斉次微分方程式から順に見ていき解の予測をしてみよう。まず微分方程式
$$\dot{x}=x \tag{28}$$
の解を予測してみる。この式は微分前後で関数が変わらないということを意味する。ということはこの微分方程式の解は $x_{(t)}=e^{t}$ のような形になりそうである。実際に与えられた微分方程式(28)式を変数分離して解いた結果からは $x_{(t)}=Ce^{t} (Cは任意定数)$ が得られる。次に微分方程式
$$\ddot{x}=x \tag{29}$$
の解を予測してみる。これは先程の考察から $x_{(t)}=Ce^{t} (Cは任意定数)$ を解に持ちそうだということがわかる。1回微分して同じならば2回微分しても同じだろうという考えだ。それともう1つ2回微分して初めて同じになるような関数は $x_{(t)}=C’e^{-t} (C’は任意定数)$ である。ここで $Ce^{t},C’e^{-t}$ は2回微分する際に互いに干渉し合わない。つまり独立なものとして考えることができる。よって与えられた微分方程式(29)式の解は
$$x_{(t)}=Ce^{t}+C’e^{-t} (C,C’は任意定数)\tag{30}$$
となる。実は解を求めるために特性方程式を立てて解の性質を調べなければならないが、ここでは雰囲気に触れてもらうのが目的なので大雑把な解説となっている。
ではいよいよ微分方程式
$$\ddot{x}=-x \tag{31}$$
の解を求める。今まで通り2回微分して-1倍になる関数を探すのだが、これまでの計算から分かると思うが2乗して $-1$ になるような数が指数関数の中に入りそうである。よって今までの計算から求める解は虚数単位を $i$ として
$$x_{(t)}=C_1e^{it}+C_2e^{-it} (C_1,C_2は任意定数) \tag{32}$$
と表されるのだろう。実際に(32)式を与えられた微分方程式(31)式に代入すれば成り立つことが分かる。しかしこれでは物理現象が見えにくいので、かの有名なオイラーの公式を使って
$$(32)=(C_1+C_2)\cos x+(C_1-C_2)i\sin x=A\cos (t+δ) (A,δは任意定数)$$
$$\begin{cases}
A^2=|x|^2=x^*x=(C_1+C_2)^2+(C_1-C_2)^2\\
δ=\text{Arctan}\hspace{1mm} \left(\dfrac{C_1-C_2}{C_1+C_2}i\right)
\end{cases}$$
と表される。一応確認だが最後は三角関数の合成をした。これは正しく単振動である。
よって今までの考察から(21亜)式
$$\ddot{θ}=-ω^2θ \tag{21亜}$$
の一般解は
$$θ_{(t)}=A\cos (ωt+δ) (A,δは任意定数)$$
となる。 $δ$ は初期位相である。こうしてみると $ω$ は角振動数であると見なせることから、単振り子は振り子の幅 $θ$ が $θ≈0$ のときには接線方向で角振動数 $ω$ の単振動をしていると見なせる。
ちょっと休憩
本記事では単振り子の運動方程式について厳密解と一般に知られている $θ≈0$ による近似解を求めてみた。調べて見たところ検索上位に出てくるようなサイトでは、厳密解を求めるために当然のようにエネルギー保存則から出発している。これは向心力のみが働く場合で角運動量を用いるのと同じように、少しでも物理的解釈を取り入れようとしているのだと思う。そう思いたい。しかしかといって単振り子でエネルギー保存則を利用した議論をしているようには見られない(少なくとも今は必要ない)ので些か謎である。初学者にとっては色々と知識を積み込まれても処理しきれないし、なぜ運動方程式から解かないのか疑問に思うところだろう。
初回
前回
次回



コメント