エネルギー保存則を立てれば簡単に求まるが……
問題
[問題初め]
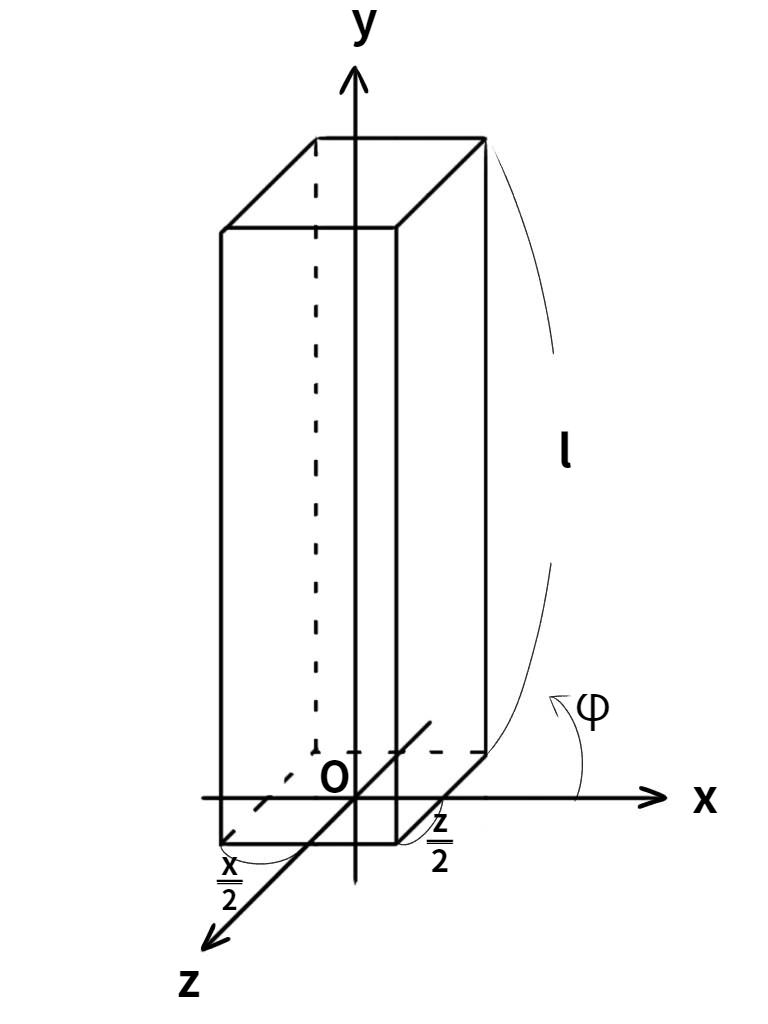
上図のように横 $x(-\frac{x}{2}≤x≤\frac{x}{2}) $ ,縦 $z(-\frac{z}{2}≤z≤\frac{z}{2})$ 、高さ $l(0≤r≤l)$ の四角柱が立てられている。四角柱の質量は $M$ で密度は一様である。高さをなす面に対する $x$ 軸からの偏角を $φ$ とする。この四角柱を静かに倒したところ $z$ 軸周りに回転した。物体には重心から $y$ 軸下向きに重力が働く。
このとき任意の成す角 $φ$ における角速度 $\boldsymbol{\omega}$ を求めよ。
[問題終わり]
前提知識
少し前に単振り子の周期 $T$ の厳密解を求めた。
今回の問題はこれを剛体にしてみたらどうなるのだろうかというものである。角速度 $\boldsymbol{\omega}$ を求められれば、そこから周期 $T$ の値は上の記事の(27)式
$$T=\frac{2π}{ω}\sum_{n=0}^∞\left(\frac{(2n-1)!!}{(2n)!!}\right)^2k^{2n} \tag{27}$$
から求まるのは勿論のこと、回転に関する量が決定されたことで更に計算の幅が広がるのだ。
この問題を解くのによくあるのがエネルギー保存則を用いる方法である。そこで運動エネルギー $\frac{1}{2}mv^2$ を慣性モーメントを用いて表現してみる。
運動エネルギーで用いる $\boldsymbol{v}$ を
の(11)式
$$\boldsymbol{v}=\boldsymbol{\omega}×\boldsymbol{r}+v_r\boldsymbol{e}_v \tag{11}$$
で消去すると
$$\frac{1}{2}mv^2=\frac{1}{2}m(\boldsymbol{\omega}×\boldsymbol{r}+v_r\boldsymbol{e}_r)^2$$
となるが、題意より $z$ 軸周りの回転は $\boldsymbol{\omega}$ は基底 $\boldsymbol{e}_z$ の方向を向くということであるから $\boldsymbol{\omega}×\boldsymbol{r}$ は基底 $\boldsymbol{e}_θ$ の方向を向く。
よって $\boldsymbol{e}_θ\cdot\boldsymbol{e}_r=0$ に注意して
$$∴ \frac{1}{2}mv^2=\frac{1}{2}m(ω^2r^2\sin^2θ+v_r^2)=\frac{1}{2}m(r\sinθ)^2ω^2+\frac{1}{2}mv_r^2 \tag{1}$$
となる。ここで $θ$ とは球座標系 $(r,θ,φ)$ における点 $\boldsymbol{r}$ に対する $z$ 軸からの偏角のことである。つまり $(r\sinθ)^2$ は点 $\boldsymbol{r}$ を $xy$ 平面上で射影した距離に当たる。
よって $z$ 軸周りの慣性モーメントを $I_z$ と置くと、(1)式は
$$\frac{1}{2}mv^2=\frac{1}{2}I_zω^2+\frac{1}{2}mv_r^2 \tag{2}$$
となる。(2)式を見れば明らかであるが、剛体の運動エネルギーとは、回転方向の運動エネルギーと進行方向の運動エネルギーの2つを考える必要があるのだ。このことはこのシリーズの第1部
の円座標系におけるエネルギー保存則(12)式
$$\frac{1}{2}m(\dot{r}^2+r^2\dot{θ}^2)+\frac{α}{r}=E_{(r,θ)} \tag{12}$$
の左辺第2項でも現れた。当記事で有効ポテンシャルの中に $\frac{1}{2}mr^2\dot{θ}^2$ を含有しているのは、ちゃんとこれがエネルギーとしての量を表すことが示されるからである。
本記事の問題設定では円運動をすることから進行方向にエネルギーは関与しない。よって考える運動方程式は回転由来のものだけで良く、(2)式より
$$\frac{1}{2}mv^2=\frac{1}{2}I_zω^2 \tag{3}$$
となる。
よくあるエネルギー保存則を使う解答
[解答初め]
$z$ 軸周りの慣性モーメントは
$$I_z=\frac{M}{xlz}\displaystyle∫_{\small{-\dfrac{x}{2}}}^{\small{\dfrac{x}{2}}}\displaystyle∫_0^l\displaystyle∫_{\small{-\dfrac{z}{2}}}^{\small{\dfrac{z}{2}}}dxdydz\hspace{1mm}(x^2+y^2)$$
$$=\frac{M}{xlz}\frac{1}{3}\left(2\left(\frac{x}{2}\right)^3+l^3\right)\cdot2\left(\frac{z}{2}\right)=\frac{M}{3}\left(\left(\frac{x}{2}\right)^2+l^2\right) \tag{4}$$
となる。よって重力が $M\boldsymbol{g}=-Mg\boldsymbol{e}_y$ であり重心の移動距離が $\displaystyle∫_{φ_0}^φ\frac{l}{2}d\boldsymbol{\varphi}=∫_{φ_0}^φ\frac{l}{2}\boldsymbol{e}_φ\hspace{1mm}dφ$ であることに注意して重心のエネルギー保存則を立てると
$$\frac{1}{2}I_zω^2=-∫_{φ_0}^φ-Mg\boldsymbol{e}_y\cdot \frac{l}{2}d\boldsymbol{\varphi}$$
$$\hspace{300px}=-∫_{φ_0}^φ-Mg\frac{l}{2}\boldsymbol{e}_y\cdot\boldsymbol{e}_φ\hspace{1mm}dφ=-∫_{φ_0}^φMg\frac{l}{2}\cosφ\hspace{1mm}dφ$$
$$\hspace{-100px}∴ Mg\frac{l}{2}\sinφ_0=\frac{1}{2}I_zω^2+Mg\frac{l}{2}\sinφ$$
$$\hspace{90px}∴ Mg\frac{l}{2}=\frac{1}{2}I_zω^2+Mg\frac{l}{2}\sinφ (∵ φ_0=\frac{π}{2}) \tag{5}$$
となる。途中の基底 $\boldsymbol{e}_y,\boldsymbol{e}_φ$ はそれぞれデカルト座標系における $y$ 軸方向の基底 $\boldsymbol{e}_y$ と球座標系における基底 $\boldsymbol{e}_φ=(-\sinφ,\cosφ)$ のことである。よって
$$ω=\sqrt{\frac{Mgl(1-\sinφ)}{I_z}} (∵ ω≥0)$$
$$=\sqrt{\frac{Mgl(1-\sinφ)}{M\dfrac{1}{3}\left(\left(\dfrac{x}{2}\right)^2+l^2\right)}}=\sqrt{\frac{3gl(1-\sinφ)}{\left(\left(\dfrac{x}{2}\right)^2+l^2\right)}} \tag{6}$$
となる。四角柱の厚み $x,z$ を無視するのなら(6)式は
$$ω=\sqrt{\frac{3g(1-\sinφ)}{l}}$$
となる。よって求める角速度 $\boldsymbol{\omega}$ は
$$\boldsymbol{\omega}=
\begin{cases}
\displaystyle\sqrt{\dfrac{3gl(1-\sinφ)}{\left(\left(\dfrac{x}{2}\right)^2+l^2\right)}}\\
\displaystyle\sqrt{\dfrac{3g(1-\sinφ)}{l}} (厚みを無視)\end{cases}\boldsymbol{e}_z \tag{7}$$
となる。
[解答終わり]
ただ重心についてエネルギー保存則を立てて、慣性モーメントの公式に則って計算したものを代入しただけである。実用的にはこちらで良いかもしれないが、これでは古典力学が理解できていなくても公式を暗記するだけで解けてしまい、面白みに欠ける。確りと古典力学の集大成らしく、今までの古典力学・数学の知識をふんだんに使って解答してみようと思う。
オイラーの運動方程式から解く
[解答初め]
剛体の重心に関するオイラーの運動方程式は角運動量を $\boldsymbol{L}$ と置いて、
$$\frac{d\boldsymbol{L}}{dt}=\boldsymbol{N}$$
$$∴ \boldsymbol{I}\dot{\boldsymbol{\omega}}=\boldsymbol{r}×\boldsymbol{F} \tag{8}$$
を解く。 $\boldsymbol{I}$ は慣性モーメントテンソルとした。
さて慣性モーメントテンソルを求める。慣性モーメントテンソルは題意の四角柱の対称性から先のエネルギー保存則で求めた慣性モーメント $I_z$ を活用して
$$\boldsymbol{I}
=\begin{pmatrix}
I_{11} & 0 & 0\\
0 & I_{22} & 0\\
0 & 0 & I_{33}
\end{pmatrix}
=\dfrac{M}{3}\begin{pmatrix}
l^2+\dfrac{z}{2}^2 & 0 & 0\\
0 & \left(\dfrac{z}{2}\right)^2+\dfrac{x}{2}^2 & 0\\
0 & 0 & \left(\dfrac{x}{2}\right)^2+l^2
\end{pmatrix} \tag{9}$$
となる。慣性乗積が全て $0$ なのは、図形的にデカルト座標系のどの基底 $(\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3)$ を回転軸にとっても、題意の図形は回転軸からその重心を通る直線について対称であることからも分かる。下の記事ではこのことを私は回転軸がブレない状態と呼んでいる。
よって角運動量 $\boldsymbol{L}$ は慣性モーメントテンソル $I_{ij}$ を用いて
$$\boldsymbol{L}=\boldsymbol{I}\boldsymbol{\omega}=I_{33}\boldsymbol{e}_3=\dfrac{M}{3}\left(\left(\dfrac{x}{2}\right)^2+l^2\right)ω\boldsymbol{e}_z \tag{10}$$
となる。これは結局 $z$ 軸周りの慣性モーメントとは慣性モーメントテンソル $I_{ij}$ の $i,j=3$ を取っただけであることが分かる。
次に重心に関するオイラーの運動方程式(8)式の右辺
$$\boldsymbol{r}×\boldsymbol{F}$$
について求める。重心の位置ベクトルは円筒座標系 $(r,φ,z)$ において $\boldsymbol{r}=\frac{l}{2}\boldsymbol{e}_r$ であり、重心には重力 $M\boldsymbol{g}=-Mg\boldsymbol{e}_y$ が掛かるから、
$$\boldsymbol{r}×\boldsymbol{F}=\frac{l}{2}\boldsymbol{e}_r×(-Mg\boldsymbol{e}_y)=-Mg\frac{l}{2}\sin\left(\frac{π}{2}-φ\right)\boldsymbol{e}_z=-Mg\frac{l}{2}\cosφ\boldsymbol{e}_z \tag{11}$$
よって(10)式、(11)式より(8)式は $ω=\frac{dφ}{dt}$ の下で
$$\dfrac{M}{3}\left(\left(\dfrac{x}{2}\right)^2+l^2\right)\dot{ω}\boldsymbol{e}_z=-Mg\frac{l}{2}\cosφ\boldsymbol{e}_z$$
$$∴ \dfrac{M}{3}\left(\left(\dfrac{x}{2}\right)^2+l^2\right)ω\frac{dω}{dφ}\boldsymbol{e}_z=-Mg\frac{l}{2}\cosφ\boldsymbol{e}_z$$
となり、この両辺を $φ$ で積分したもの
$$∴∫_{ω_0}^ω\dfrac{M}{3}\left(\left(\dfrac{x}{2}\right)^2+l^2\right)ω\boldsymbol{e}_z\hspace{1mm}dω=∫_{φ_0}^φ-Mg\frac{l}{2}\cosφ\boldsymbol{e}_z\hspace{1mm}dφ$$
は正しくエネルギー保存則に該当する。よって以降は前半の解答に帰着する。
[解答終わり]
終わりに
今回は剛体の運動についての例題を解いてみた。早い話が剛体になるということは、剛体に掛かる力の場所と向きをより厳密に扱う必要があり、更に回転運動を考慮する必要があるというだけのことである。これを理解してしまえば、大抵の質点の問題を剛体の運動に置き換えたものは解けてしまう。運動方程式を立てるのでも良いし、エネルギー保存則を立てるのでも良いのだ。本記事で慣性モーメントの素晴らしさが少しでもわかってもらえれば嬉しい。
いつか摩擦のある斜面を移動する運動を取り上げてみようと思う。これはオイラーの運動方程式とニュートンの運動方程式が i)オイラーの運動方程式のみが釣り合いの式となる場合と、ii)ニュートンの運動方程式のみが釣り合いの式となっている場合とで運動が異なる。i)のときには物体が滑るが、ii)のときには物体は転がる。



コメント