本記事はシリーズ「量子力学を学ぶために必要な基本的な考え方」の第1部となっています。第1部では前期量子論で取り扱われる量子の二重性と、量子力学の根底にあるシュレディンガー方程式を解説していきます。
初回
これ
次回
初めに
量子力学は微小な物体における物理現象を記述するための物理学の一分野です。古典力学では物体の運動を質点として記述し、それが受ける力はニュートンの運動方程式で表されます。しかし原子や分子などの微小な物体に対してはこのような記述は限界があります。量子力学では物質が粒子としての性質と波動としての性質を併せ持つことが認められ、波動関数という概念が導入されます。
波動関数は物質の状態を数学的に表現する関数であり、この関数から物質のあらゆる物理量が求められます。ただし波動関数の形状自体は観測によって決定され、それが古典的な物理量として観測されることになります。
量子力学には複数の重要な原理や法則が存在します。例えば波動関数の時間発展を記述するシュレディンガー方程式があります。また量子力学においては測定を行うことで系の状態が変化することが認められており、この現象は観測者効果と呼ばれます。またエネルギーと時間の不確定性原理や、量子力学的相互作用の強さを表す結合定数なども重要な概念です。
量子力学は原子物理学や素粒子物理学などの分野で重要な役割を果たしています。また量子コンピューターや量子暗号などの応用分野も注目を集めています。
本記事では量子力学を記述する重要な方程式であるシュレディンガー方程式について簡単に紹介しています。
シュレディンガー方程式の大まかな概要
物質の本質はなんだ
マクロな視点では物質はモノとして捉えられる。しかしこれをミクロな視点で観察すると単純なモノとして扱うには奇妙な振る舞いを見せるのだ。
具体的に水を想像してみてほしい。マクロにとらえるのなら、水は川のように流れ、雨のように降らせる。ある一定の温度まで冷やせば氷となって固まり、またある一定の温度まで温めれば蒸気となって宙を自在に動き回る。この水を限りなく小さく取り出したら何が残るのだろうか。
読者の方ならすぐに分かるはずだろう。水は $H_2O$ という水分子で構成されているのである。これよりもミクロに見てみると、分子は原子がくっついたものであることが分かる( $H_2O$ なら3つ)。その周りには電子が一定の間隔で滞在している。
……というのが高校までで勉強してきた常識である。この物質を構成するモノは原子や電子等の粒子であるという認識は尤も自然である。しかしなながら現実はそう単純に解明されるものではなく、20世紀頃までの学者を悩ませる問題であった。
粒子と波動の二重性
光の本質は粒子か波動かという議論はホイヘンスとニュートンにより17世紀頃から長らく3年以上も続いた。19世紀後半以降は光や電子以外にもこの粒子と波動の二重性が認められ、20世紀初頭には二重性を併せ持つ「量子」の存在が仮定され、これについて議論する量子論が提唱された。その後20世紀末期には粒子と波動の二重性の正確な定量もなされ、現代では古典的な粒子説・波動説の欠点を補い、微小系の振る舞いを記述できる。量子論は現代物理学の基礎的な枠組みの一つとなり、宇宙論や素粒子物理学など様々な分野で応用されている。
シュレディンガー方程式の導出みたいなやつ
光には波動の性質を持つ。電磁気学のマクスウェル方程式によれば電磁波の波動方程式を導出できた。特に以下の記事
において自由空間における電磁波の波動方程式
$$\dfrac{1}{c^2}\dfrac{∂^2}{∂t^2}\boldsymbol{A}-\Delta\boldsymbol{A}=\boldsymbol{0}$$
を導出した。このことから量子の波動の性質を示す方程式は
$$\zeta\dfrac{∂^2}{∂t^2}\boldsymbol{\varphi}=\Delta\boldsymbol{\varphi}$$
のように書き表されると推測したいところだが、実際に波動
$$\boldsymbol{\varphi}_{(\boldsymbol{r},t)}=\boldsymbol{\varphi}_0e^{i(\boldsymbol{k}\cdot\boldsymbol{r}-\omega t)}$$
の $t$ の2階偏微分と $r$ の2階偏微分を比較すると
$$\begin{cases}
\dfrac{∂^2\varphi}{∂t^2}=-\omega^2\boldsymbol{\varphi}\\
\Delta\boldsymbol{\varphi}=-k^2\boldsymbol{\varphi}
\end{cases} $$
となる。これが単なる波動なら問題なく波動方程式を満足するのだが、今考えているのは量子であるから波動と粒子の二重性を考慮しなければならない。つまりド・ブロイ波
$$\begin{cases}
E=h\nu=\omega\hbar\\
p=\dfrac{h}{\lambda}=k\hbar
\end{cases} \tag{1}$$
の条件( $p$ は運動量、 $E$ はエネルギー、 $\nu$ は振動数、 $h$ はプランク定数、 $\hbar=\frac{h}{2π}$ はディラック定数)が成り立つ必要がある。このとき波動関数に代入すると
$$E^2=c^2p^2$$
となってしまい、ド・ブロイ波と矛盾する。その代わりに
$$\begin{cases}
i\hbar\dfrac{∂\boldsymbol{\varphi}}{∂t}=E\\
\dfrac{1}{2m}\left(\hbar^2\Delta\right)\boldsymbol{\varphi}=E\boldsymbol{\varphi}
\end{cases}$$
が成り立つことを黙認してほしい( $i$ は虚数単位、 $\varphi$ は波動関数、 $m$ は質量)。この式の意味自体はよく分からないのだが、どうも上手い具合に成り立つのである。
ここでエネルギー $E$ について運動量 $p=mv^2$ を用いて
$$E=\dfrac{1}{2}mv^2=\dfrac{p^2}{2m}$$
と表される。
このとき分散関係は
$$\begin{align*}
E&=\dfrac{p^2}{2m}\\
∴ \hbar\omega&=\dfrac{\hbar^2k^2}{2m}\\
∴ \omega&=\dfrac{\hbar k^2}{2m}
\end{align*}$$
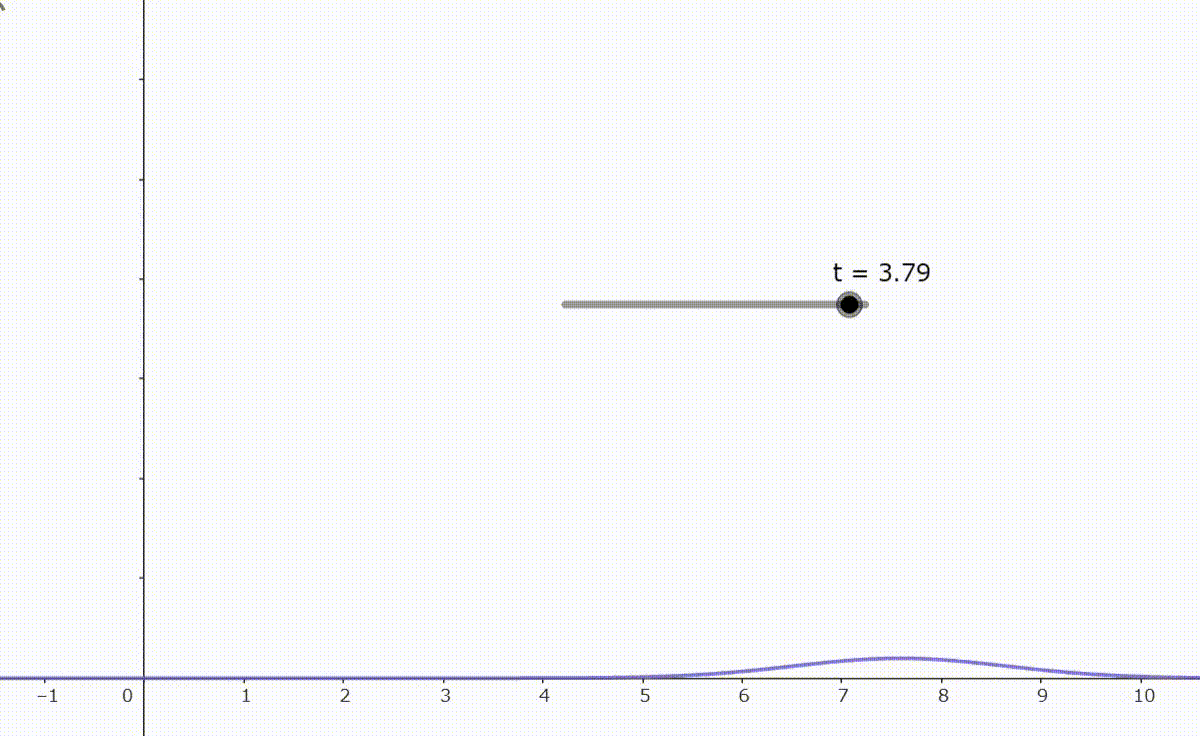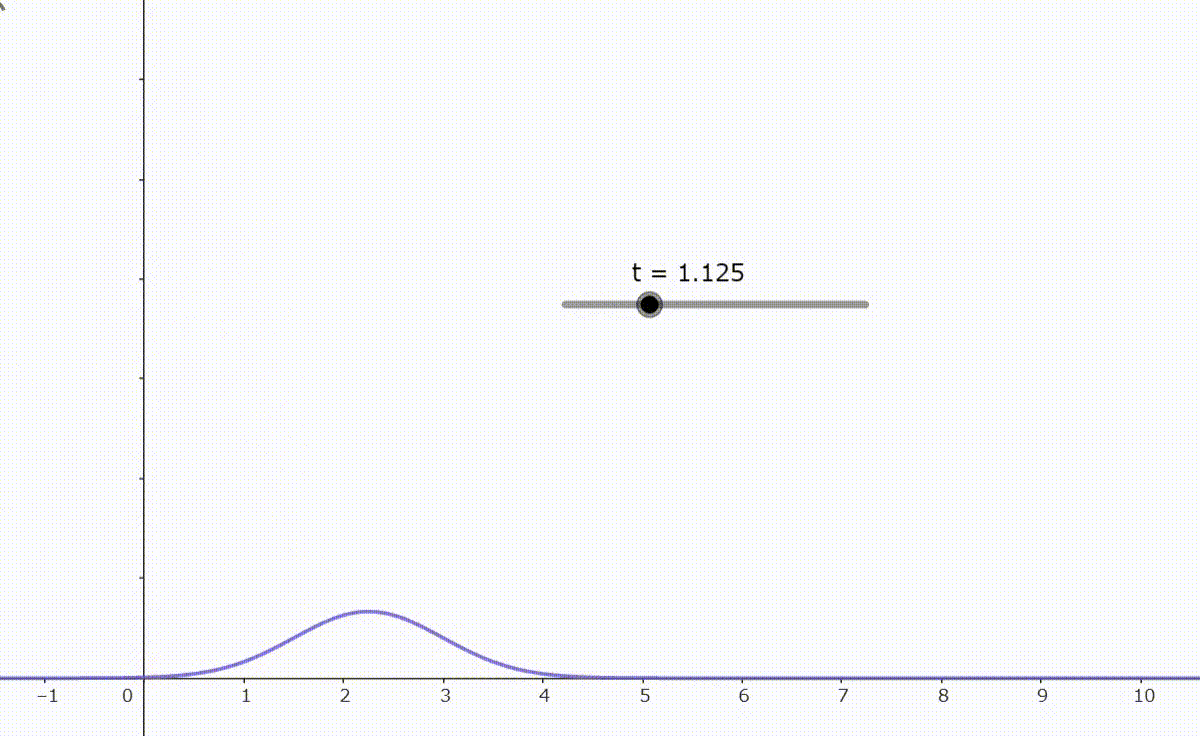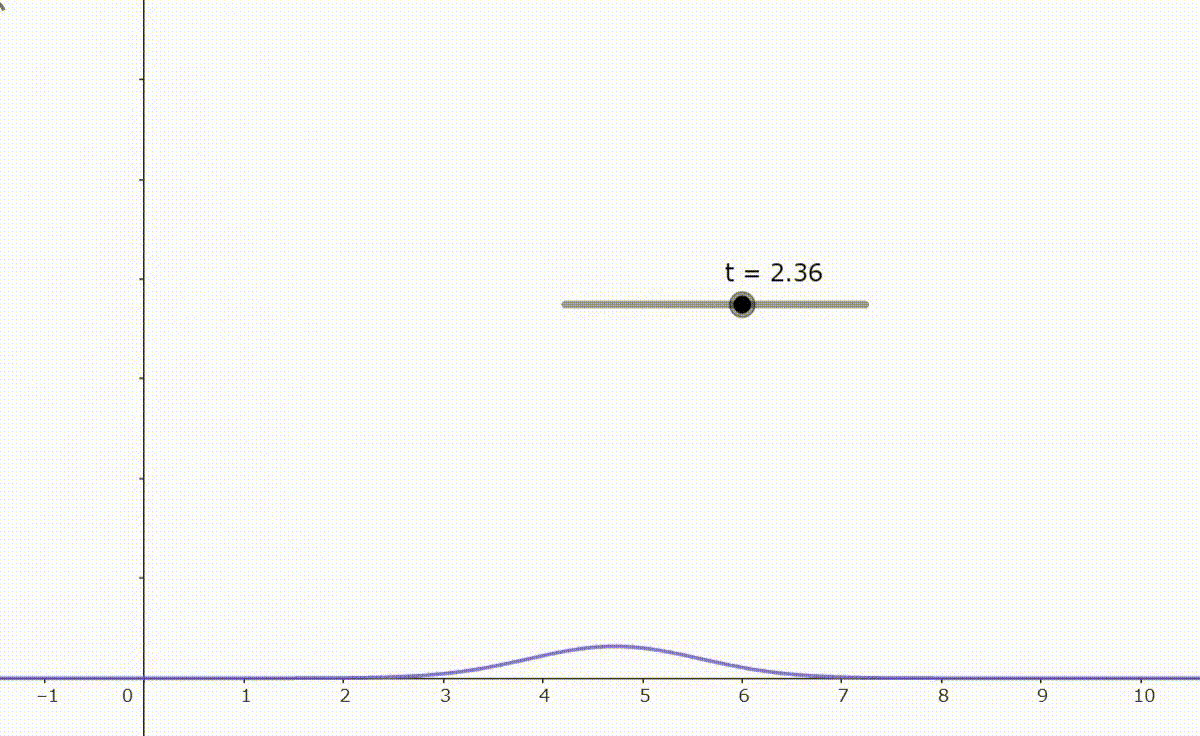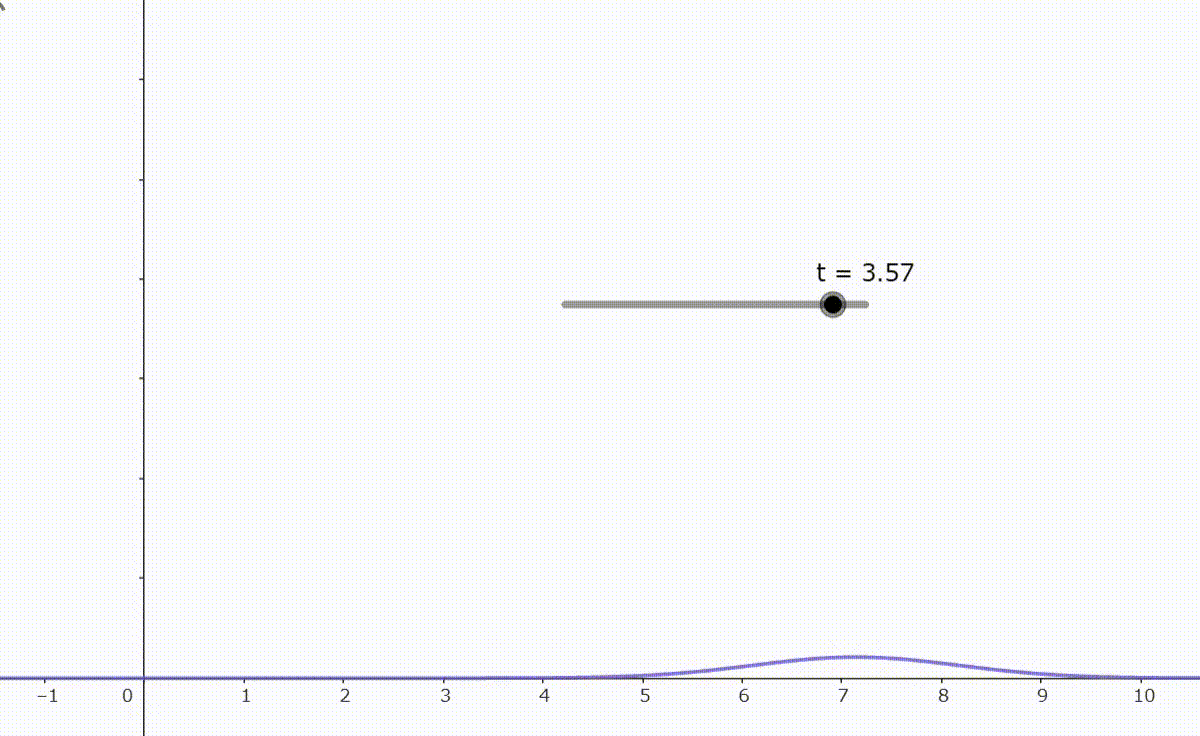
となる。右図は発散がある波束の時間変化を示す。
よって量子論では一般に波動関数 $\boldsymbol{\varphi}$ によって形成される波束は時間変化によって自由空間を広がっていくことが分かる。このことから $t=0$ のときの波束は最小不確定状態となり、コヒーレント状態になる。
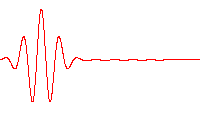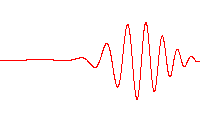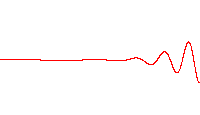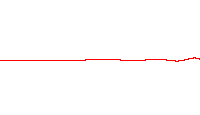
出典:Wiki
この表現方法に見立てて、運動量 $p$ を得るための演算子を $\hat{p}$ と置くと、ポテンシャルの働かない空間におけるエネルギー $E$ は演算子 $\hat{p}$ における固有方程式
$$E|\varphi\rangle=\dfrac{\hat{p}^2}{2m}|\varphi\rangle \tag{2}$$
として表現することができる。つまり固有方程式(2)式で固有値を求めるということは、それぞれの固有関数 $\boldsymbol{\varphi}_k$ におけるエネルギーが定値 $E_k$ として観測されたものであると解釈することができる。ただし $|\varphi\rangle$ はブラ-ケット記法で、詳しくは以下の記事
で解説しているので知らない人は参照するように。こちらのシリーズでは固有方程式の考え方も載せているので興味がある方は一読されたい。
そこで具体的に $\hat{p}$ の示す量を調べるために波動関数 $\boldsymbol{\varphi}$ を $\nabla$ で勾配取ると
$$\begin{align*}
\nabla\boldsymbol{\varphi}&=ik\boldsymbol{\varphi}=i\dfrac{p}{\hbar}\boldsymbol{\varphi}\\
∴ \hat{p}&=-i\hbar\nabla
\end{align*}$$
となる。よって一般にポテンシャル $V_{(\boldsymbol{r})}$ が働く場合には全エネルギー $E$ は
$$\left(\dfrac{\hat{p}^2}{2m}+\hat{V}\right)|\varphi\rangle=E|\varphi\rangle$$
を満たす。 $\hat{V}$ はポテンシャル $V_{(\boldsymbol{r})}$ を与えるポテンシャル演算子とした。ここで左辺をハミルトン演算子
$$\hat{H}:=\dfrac{\hat{p}^2}{2m}+\hat{V} \tag{3}$$
と置くと、波動関数 $|\varphi\rangle$ は固有方程式
$$\hat{H}|\varphi_{(\boldsymbol{r})}\rangle=E|\varphi_{(\boldsymbol{r})}\rangle \tag{4}$$
を満たす。よってシュレディンガー方程式は以下の時間に依存する場合(上式)と依存しない場合(下式)に区別される。
$$\begin{align*}
i\hbar\dfrac{∂}{∂t}|\varphi_{(\boldsymbol{r},t)}\rangle&=\hat{H}|\varphi_{(\boldsymbol{r},t)}\rangle \tag{5.1}\\
\hat{H}|\varphi_{(\boldsymbol{r})}\rangle&=E|\varphi_{(\boldsymbol{r})} \tag{5.2}\rangle
\end{align*} \tag{5}$$
(5)式の上式は時間依存する場合のシュレディンガー方程式で、左辺と右辺とでそれぞれ時間の偏微分と空間の偏微分で分離されている。このとき定数 $E$ とは下式の右辺の固有値 $E$ と一致する。つまりあからさまにハミルトン演算子 $\hat{H}$ が時間に依存しない場合には、シュレディンガー方程式の空間に関して微分方程式(5.2)式だけを取り出すことが可能である。このことから波動関数 $|\varphi\rangle$ の時間変化に関しては、波動関数の各固有状態 $|\varphi_{(E_k)}\rangle$ に対応する固有エネルギー $E_k$ の状態に影響を及ぼさない。
ところでシュレディンガー方程式の解説途中でハミルトン演算子を
$$\hat{H}:=\dfrac{\hat{p}^2}{2m}+\hat{V} \tag{3}$$
と置いた。この演算子を見ても明らかではあるが、ハミルトン演算子とは全エネルギー $E$ を得るための演算子である。ここで解析力学においてはハミルトニアン $\mathcal{H}$ は一般化座標 $q$ と一般化運動量 $p$ において
$$\mathcal{H}_{(q,p;t)}=T+V$$
と定義される( $T$ は運動エネルギー、 $V$ はポテンシャルエネルギー)。ハミルトニアンは物理系における全エネルギーを表していて、解析力学では一般化座標の時間微分 $\dot{q}$ と一般化運動量の時間微分 $\dot{p}$ は正準変換と呼ばれる式
$$\begin{cases}
\dot{q}_i=\dfrac{∂\mathcal{H}}{∂q_i}\\
\dot{p}_i=-\dfrac{∂\mathcal{H}}{∂p_i}\\
\end{cases}$$
等でよく使われる。この式を方程式として正準方程式を解くことで系の時間発展を調べることが可能である。この考え方は系の状態を考えていることから熱力学でも広く使われている。
ちょっと休憩
本記事では量子力学を議論するために要となるシュレディンガー方程式が何を意味しているのか簡単に紹介した。次回ではシュレディンガー方程式で使われるハミルトン演算子 $\hat{H}$ や波動関数 $|\varphi\rangle$ についてもう少し詳しく見ていこうと思う。
初回
これ
次回



コメント