高校数学ではベクトルの計算をさせられたが……
高校数学ではベクトルの計算をさせられた。例えばベクトルの内積とは2つのベクトルの従属度合いによって定まる量であった。このことは以前記事
で書いたので、この人何言っているんだと思う読者は是非一読してほしい。この記事にあるように高校数学で習う内積とは実ベクトルの内積であるのだが、高校数学では扱うベクトルが幾何実ベクトルであることは暈される(超絶どうでも良い話だが暈すという漢字が量にそっくりであるということに感動を覚えた自分に驚いた)し、ベクトル以外に内積の計算があるという事実さえ知らされないことも十分にあり得る。
「いや内積はベクトル方程式で活躍するっしょ?」
などと思われる読者もいるかもしれない。確かに活躍はするのだが、内積を道具として扱えるのがベクトル同氏の成す角を考えるときくらいしかないというだけにすぎないのだ。結局内積を定義した背景は曖昧なままである。
ここではベクトルの計算・行列の計算をする以前にベクトル・行列を写像という立場から考えるに至った経緯を紹介していこうと思う。
写像の定義
少し前の先輩方(1998年度~2007年度)は複素数平面の代わりに数学Cで行列を習った。もう少し前の先輩方(1989年度~1997年度)は数学Cで複素数平面と行列を習った。しかし大学受験数学で扱う行列はなんかよく分からない計算をさせられるだけである。ここではそんな諸計算のことは一旦置いておき、もっと俯瞰して写像という立場から行列を見ていこうと思う。
写像と函数
集合 $X$ の各元に対してそれぞれ集合 $Y$ の元をただひとつずつ指定するような規則 $f$ が与えられているとき、$f$ を「集合 $X$ の各元 $x_i$ から集合 $Y$ の各元 $y_i$ への写像」と言い、一般にこれを
$$f:X→Y , X\xrightarrow{f}Y$$
等と表す。イメージとしては右図のように集合 $X$ の各元 $x_i$ を函 $f$ に入力したら別の集合 $Y$ の各元 $y_i$ へとそれぞれ1つづつ別の値に出力された状態と言えよう。このとき出力される各元 $y_i$ の値は入力される各元 $x_i$ によって必ず異なる値を取らなければいけないわけではない。
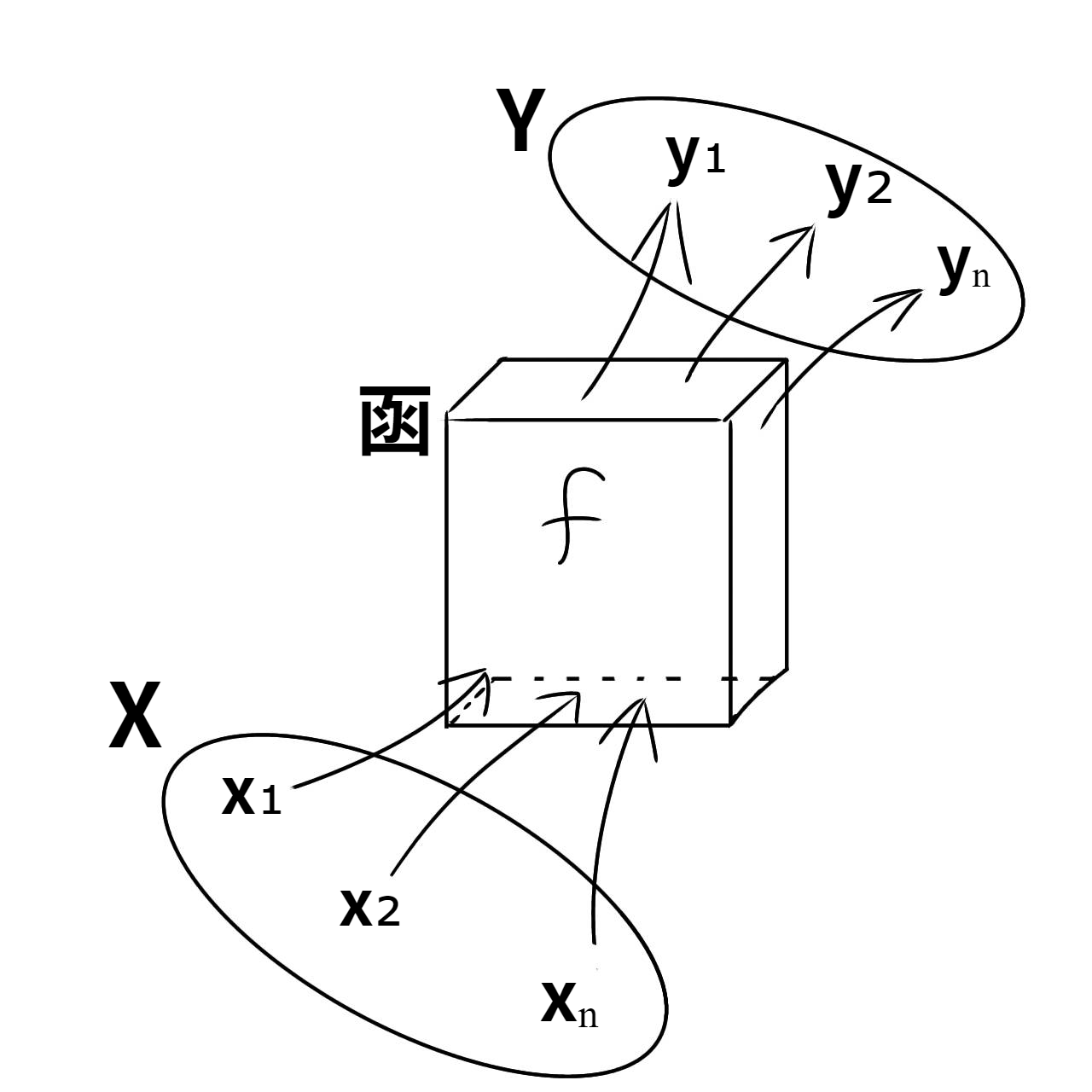
また各元について注目して
$$x_i↦f(x_i)=y_i$$
等と書かれることもある。
そこで写像を大きく全射・単射・全単射の3つに分類することができる。
全射とは「集合 $X$ の全ての元 $x_i$ を写像 $f$ によって集合 $Y$ の各元 $y_i$ のいずれかに変換し、かつ全ての元 $y_i$ が何かしらの元 $x_i$ から変換される」場合のときを指す。
単射とは「集合 $X$ の全ての元 $x_i$ を写像 $f$ によって集合 $Y$ の各元 $y_i$ のいずれかに変換し、かつ元 $x_i$ が異なる場合には元 $y_i$ の取る値はすべて異なる」場合のときを指す。
全単射とは「全射と単射の2つの性質を持つ」場合のときを指す。全単射はよく「集合 $X$ の各元 $x_i$ と集合 $Y$ の各元 $y_i$ は1対1で対応する」等と言われる。
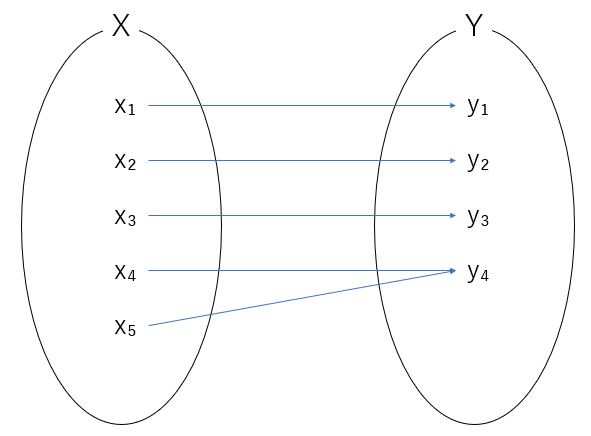
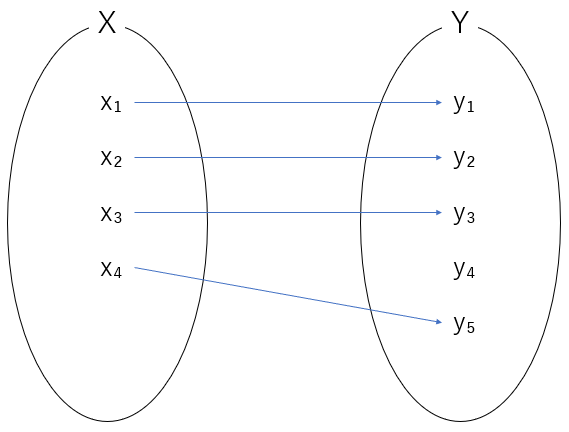
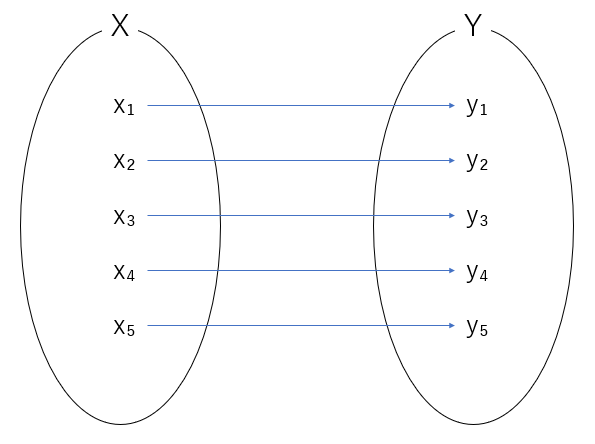
一般的に関数とは各元が数であるものを指すと理解されている。つまり数を函で入出力することが函数なのである。この「函」という漢字は元来中国語から翻訳したときのもので、現在は「関」を当てていることに注意されたい。
線型写像と線型変換
特に考える元をベクトルとし、この集合をベクトル空間 $V$ とする。このとき任意のベクトル $\boldsymbol{x},\boldsymbol{y}∈V$ についてベクトル空間 $V$ からベクトル空間 $W$ への写像 $f$ について、
$$\begin{align*}f(\boldsymbol{x}+\boldsymbol{y})&=f(\boldsymbol{x})+f(\boldsymbol{y}) (加法性)\\
f(c\boldsymbol{x})&=cf(\boldsymbol{x}) (斉次性)\end{align*} \tag{1}$$
を満たすとき、 $f$ を線型写像と言う。この2つの性質を線型性と呼ぶ。特に写像 $f$ が同一のベクトル空間 $V$ で作用している場合には線型変換と言う。
線型写像 $f$ となり得る対象を調べる
$n$ 次ベクトル $\boldsymbol{x}$ で構成される空間を $n$ 次ベクトル空間 $\mathbb{K}^n$ とし、 $m$ 次ベクトル $\boldsymbol{y}=f(\boldsymbol{\boldsymbol{x}})$ で構成される空間を $m$ 次ベクトル空間 $\mathbb{K}^m$ とする。このとき写像 $f$ となり得る対象を調べたい。
そこで $T$ をそれぞれのベクトル空間 $V→W$ についての基底 $\left\{\boldsymbol{e}_1,\boldsymbol{e}’_2,\cdots,\boldsymbol{e}’_n\right\},\left\{\boldsymbol{e}’_1,\boldsymbol{e}’_2,\cdots,\boldsymbol{e}’_m\right\}$ における写像を表現する作用素と名付けることにする。
よって写像 $f$ によって $n$ 次ベクトル $\boldsymbol{x}$ から $m$ 次ベクトル $\boldsymbol{y}$ に変換するということは、作用素 $T$ を用いて
$$\boldsymbol{y}=T\boldsymbol{x} \tag{2}$$
という変換をするということである。このとき当然ながら作用素 $T$ は(1)式の線型性から $f(\boldsymbol{x})$ を $T\boldsymbol{x}$ に書き換えた
$$\begin{align*}
T(\boldsymbol{x}+\boldsymbol{y})&=T\boldsymbol{x}+T\boldsymbol{y} (加法性)\\
T(c\boldsymbol{x})&=cT\boldsymbol{x} (斉次性)
\end{align*} \tag{3}$$
が成り立つことが認められる。
また2つのベクトル $\boldsymbol{x},\boldsymbol{y}$ がそれぞれ有限なベクトル空間 $V,W$ の基底 $\left\{\boldsymbol{e}_1,\boldsymbol{e}’_2,\cdots,\boldsymbol{e}’_n\right\},\left\{\boldsymbol{e}’_1,\boldsymbol{e}’_2,\cdots,\boldsymbol{e}’_m\right\}$ の線型結合で
$$\boldsymbol{x}=\begin{pmatrix}a_1\\a_2\\\vdots\\a_n\end{pmatrix},\hspace{10px}
\boldsymbol{y}=\begin{pmatrix}b_1\\b_2\\\vdots\\b_m\end{pmatrix} \tag{4}$$
のように列ベクトルで表されるものとする。ここで出た $a_i,b_j$ は体 $\mathbb{K}$ 上に属する定数で、2つのベクトル $\boldsymbol{x},\boldsymbol{y}$ 自体がそれぞれ $n,m$ 個の基底による線型変換
$$\boldsymbol{x}=\begin{pmatrix}\boldsymbol{e}_1 & \boldsymbol{e}_2 & \cdots & \boldsymbol{e}_n\end{pmatrix}
\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix},
\hspace{10px}\boldsymbol{y}=\begin{pmatrix}\boldsymbol{e}’_1 & \boldsymbol{e}’_2 & \cdots & \boldsymbol{e}’_m\end{pmatrix}
\begin{pmatrix}b_1 \\ b_2 \\ \vdots \\ b_m\end{pmatrix} \tag{5}$$
となっている。そのためそれぞれのベクトル $\boldsymbol{x},\boldsymbol{y}$ が $n$ 次ベクトル空間 $\mathbb{K}^n$ 、 $m$ 次ベクトル空間 $\mathbb{K}^m$ で構成されるのだ。
なお(4)式と(5)式は2つのベクトル $\boldsymbol{x},\boldsymbol{y}$ について異なる表現をしていることに注意されたい。(4)式はベクトルの基底を無視して単に列ベクトルとして表記しているのに対し、(5)式は基底の線型結合で表記しどんな基底を取っているのか分かるようにしてある。
そこで $V→\mathbb{K}^n$ の変換を線型変換 $φ$ とし、$W→\mathbb{K}^m$ の変換を線型変換 $φ’$ とする(右図)と、ベクトル空間 $\mathbb{K}^n→\mathbb{K}^m$ への作用素は
$$φ’◦T◦φ^{-1}$$
となる。
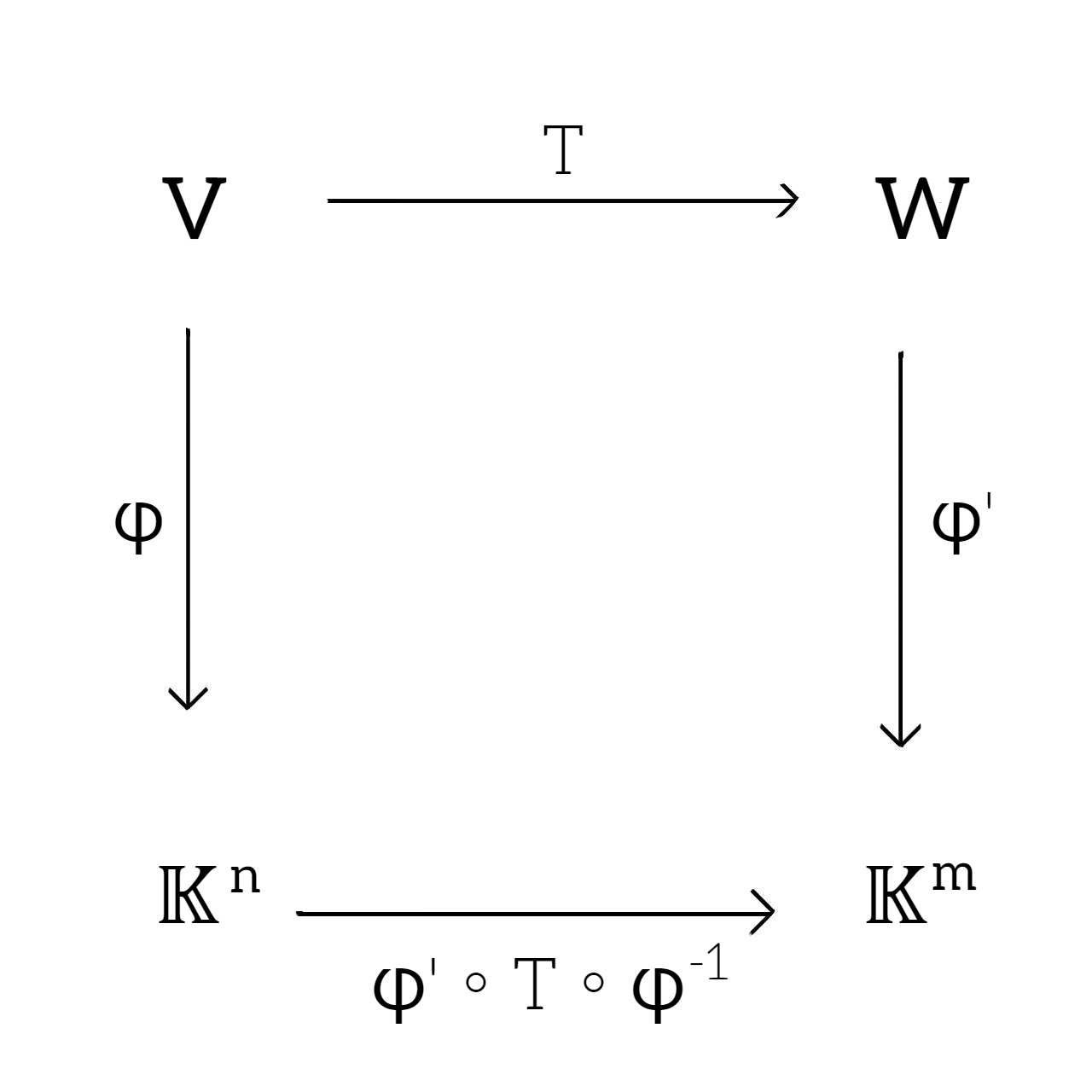
またこのとき(2)式は各基底による線型変換に注意して
$$\begin{align*}
(2):\boldsymbol{y}&=T\boldsymbol{x}\\
∴ φ’\boldsymbol{y}&=φ'(T\boldsymbol{x})\\
&=φ’◦T\boldsymbol{x}\\
&=φ’◦T◦(φ^{-1}◦φ)\boldsymbol{x}\\
&=(φ’◦T◦φ^{-1})(φ\boldsymbol{x})\\
∴ \begin{pmatrix}b_1\\b_2\\\vdots\\b_m\end{pmatrix}
&=(φ’◦T◦φ^{-1})\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}
\end{align*} \tag{6}$$
となる。よって線型写像 $f$ となり得る対象は作用素が
$$φ’◦T◦φ^{-1}$$
であり、これは $(m,n)$ 型の行列
$$\boldsymbol{A}=\begin{pmatrix}
A_{11} & A_{12} & \cdots & A_{1n}\\
A_{21} & A_{22} & \cdots & A_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
A_{m1} & A_{m2} & \cdots & A_{mn}\\
\end{pmatrix} \tag{7}$$
によって表現される。一般にこの行列は表現行列 $\boldsymbol{A}$ と名付けられる。この行列の各要素 $(i,j)\hspace{10px}(i≤m,j≤n)$ を $A_{ij}$ として表記すれば表現行列 $\boldsymbol{A}$ は2階のテンソルとなる。
ここで $\mathbb{K}^n→\mathbb{K}^m$ の写像 $f$ を表す表現行列 $\boldsymbol{A}$ であるが、逆写像 $f^{-1}$ が存在する写像 $f$ は単射であり、特に線型写像において全単射となる写像を同型写像と言う。
つまり $\mathbb{K}^n→\mathbb{K}^n$ のように同じ基底配列のベクトルに変換する写像 $φ=φ’$ の場合には、写像 $f$ は同型写像となり、表現行列 $\boldsymbol{A}$ は $n$ 次正方行列になる。
テンソルの階数を弄ってみる
ここでテンソルの階数を落としたらどうなるのか気になることだろう。このテンソル $A_{ij}$ について恒常的に $i=1$ となるとき、表現行列 $\boldsymbol{A}$ は $(1,n)$ 型の行ベクトル
$$\boldsymbol{A}=\begin{pmatrix}A_1 & A_2 & \cdots & A_n \end{pmatrix}$$
となる。これは1階のテンソル $A_j$ である。よって(6)式で得られる $\boldsymbol{y}$ はベクトル $\boldsymbol{A}$ を実ベクトルとして2つのベクトル $\boldsymbol{A},\boldsymbol{x}$ の内積
$$\boldsymbol{A}\cdot\boldsymbol{x}=\begin{pmatrix}A_1 & A_2 & \cdots & A_n \end{pmatrix}
\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}$$
となる。更にテンソル $A_j$ について恒常的に $j=1$ となるときには、スカラー
$$\boldsymbol{A}=A$$
となる。これは0階のテンソルである。よって(6)式で得られる $\boldsymbol{y}$ はベクトル $\boldsymbol{x}$ と平行なベクトルとなる。
逆に新しく行列 $\boldsymbol{A}$ に階(私はそう呼ぶが)の要素を加えた行列階を定義すれば、これは3階のテンソル $A_{ijk}$ となる $(k≤l)$ 。例えばベクトル $\boldsymbol{x}$ から $(m,l)$ 型の行列 $\boldsymbol{y}$ を求めたいのなら
$$\begin{align*}\begin{pmatrix}
b_{11} & b_{12} & \cdots & b_{1l}\\
b_{21} & b_{22} & \cdots & b_{2l}\\
\vdots & \vdots & \ddots & \vdots\\
b_{m1} & b_{m2} & \cdots & b_{ml}\\
\end{pmatrix}
&=\begin{pmatrix}
A_{11} & A_{12} & \cdots & A_{1n}\\
A_{21} & A_{22} & \cdots & A_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
A_{m1} & A_{m2} & \cdots & A_{mn}\\
\end{pmatrix}_k
\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}\\
∴ y_{jk}&=A_{ijk}x_i\end{align*}$$
となる。最後はテンソルを用いて表現した。最初の添え字 $_k$ は $k$ 階における行列の断面図となっている。そのため行列のように幾何概念を取り入れるのなら、行列階は幾何学的に直方体上に並べられる。そのためいくら頑張っても平面に描くのは困難ではあるが、平面に $k$ 枚刻みの断面図を列ベクトルのように(本当は階行列ベクトルになるが)並べることで、テンソルを用いた表現が遥かに視覚的にも直感的にも理解しやすくなる。
これ以上の階数についても同様に定義してあげれば考えることができる。 $\boldsymbol{A}$ が多次元配列となっても線型写像
$$\boldsymbol{y}=\boldsymbol{A}\boldsymbol{x}$$
のように書けるのである。
線型変換の場合
ベクトル空間 $W$ が $V$ と一致するとき、つまり写像 $f$ が $V$ の線型変換で表されるときには同型写像 $φ,φ’$ は同様に $V→\mathbb{K}^n$ の変換となる。よって線型変換の場合には変換前後で基底を取り換えずに $φ=φ’$ とすることができる。この恩恵は大きく、例えばデカルト座標系においてベクトルの対称移動、回転移動をしたいときには、これに対応した表現行列 $\boldsymbol{A}$ をベクトルに左から添えるだけで良いのだ。
例えば3次元のベクトル $\boldsymbol{x}$ を $z$ 軸周りに $θ$ だけ回転させて、更に $x$ 軸について対称移動させたベクトル $\boldsymbol{y}$ は
$$\boldsymbol{y}=
\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & -1\\
\end{pmatrix}
\begin{pmatrix}
\cosθ & -\sinθ & 0\\
\sinθ & \cosθ & 0\\
0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix}a_1 \\ a_2 \\ a_3\end{pmatrix}$$
となり、行列を用いるとかなりすっきりと書ける。
最後に
この記事では写像という概念を持ち出して線型代数における行列の立ち位置を俯瞰的に見てみた。ベクトルや行列は結局のところテンソルにおいて階数を指定しただけに過ぎないのである。ベクトルや行列はその中でもより図形的に解釈がしやすいので、広く学習がされているのだと推測できる。



コメント