本記事は
に続く。
三角関数と双曲線関数と複素指数関数
三角関数と双曲線関数の定義
まず三角関数を
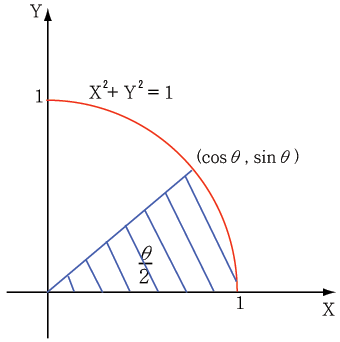
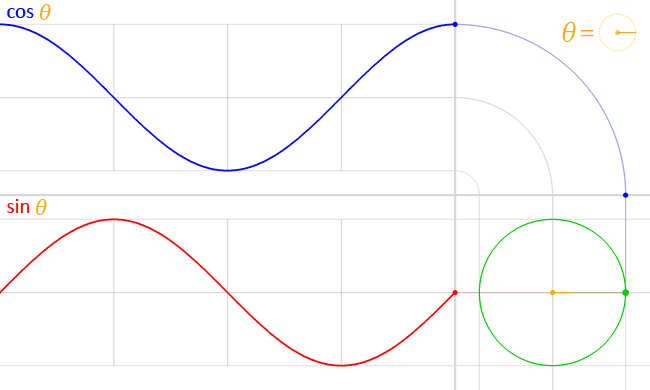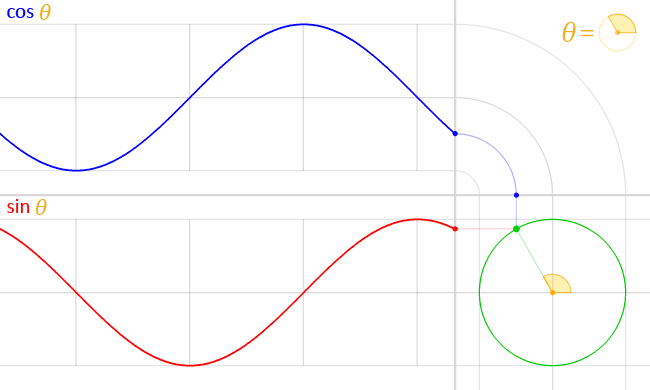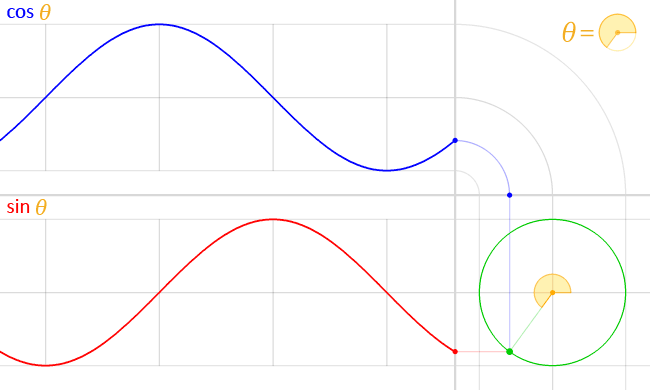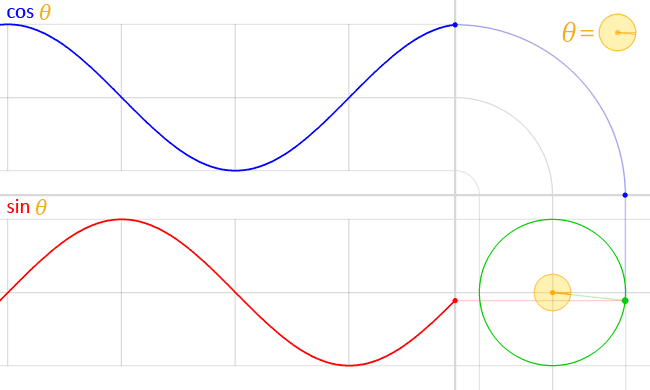
原点を中心とする半径1の円 $x^2+y^2=1$ 周上の点 $(x,y)$ を $(\cosθ,\sinθ)$ と置き、更に
$$\frac{y}{x}=\frac{\sinθ}{\cosθ}=\tanθ$$
と置く。このとき
$$\begin{cases} \cosθ\\ \sinθ\\ \tanθ \end{cases}$$
斜線の領域の面積が θ /2 の時の単位円周上の座標が (cos θ, sin θ)
出典:Wiki正円より得られる cosθ と sinθ
出典:Wikiで表される $θ$ についての関数の総称
と定義する。この定義から三角関数は円関数とも呼ばれる。
これに変えて双曲線関数を
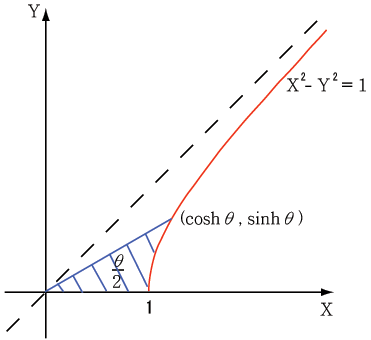
原点を対称とする双曲線 $x^2-y^2=1$ の周上の点 $(x,y)$ を $(\coshθ,\sinhθ)$ と置き、更に
$$\frac{y}{x}=\frac{\sinhθ}{\coshθ}=\tanhθ$$
と置く。このとき
$$\begin{cases} \coshθ\\ \sinhθ\\ \tanhθ \end{cases}$$
で表される $θ$ についての関数の総称
斜線の領域の面積が θ /2 の時の双曲線上の座標が(cosh θ, sinh θ)
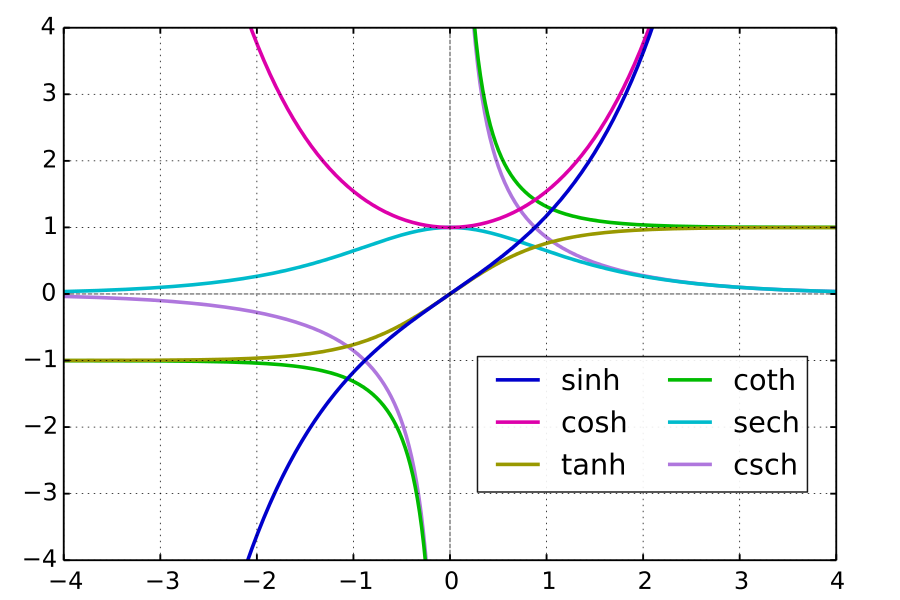
出典:Wiki6つの双曲線関数 (sinh, cosh, tanh, coth, sech, csch) のグラフ
出典:Wiki
と定義する。
関数の冪級数展開による表現
このように三角関数の定義のように自然な形で双曲線関数を定義することができた。しかしこれらの関数のグラフが本当に上図のようになるのか確かめる手段が無い。有名角ならまだ作図して求められることもあるが、例えば $\sin(π/180)$ などは具体的に求めるのは難しい。そこでこれらの関数が
$$\sin x=\sum_{n=0}^∞ a_nx^n$$
のように冪級数展開できると信じてみることにする。冪級数展開できるのならば具体的な値を代入して計算することができる。
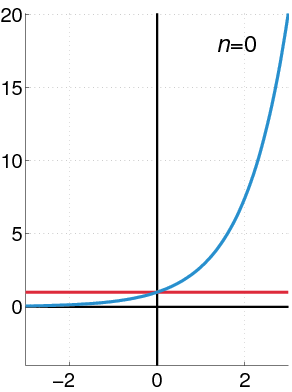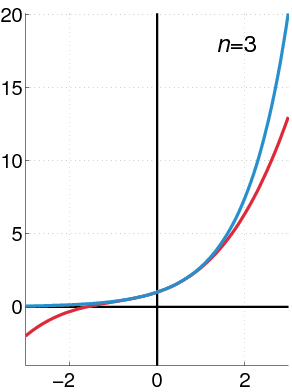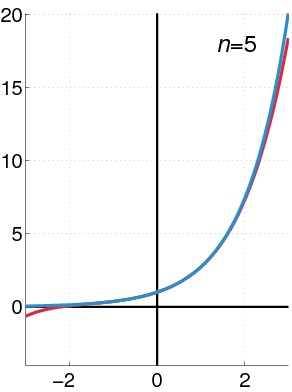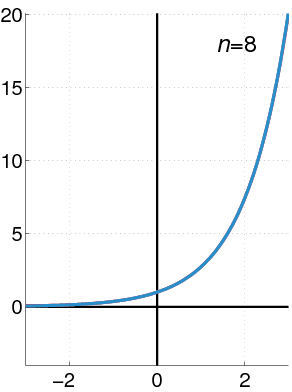
そこでまずは $n=1$ のときの $\sin x$ の冪級数(これを冪級数というのかは疑問であるが)を調べる。つまり多分 $n>>1$ (級数がもっと多い)であろう関数を無理矢理1次式 $x$ で近似してやろうというものだ。これを $n=1,2,3,\cdots$ と増やしていけば、きっと与えられた関数と同等の式が得られるのだろうという思いである。
$n$ 次近似曲線の導出
以下では冪級数展開をするために $n$ 次近似ができないか探している。高校数学で扱われた1次近似以降を導出しようというものだ。さて想起しよう。微分の定義から出発する。
関数 $f(x)$ が実数 $x$ 内の閉区間において極限
$$\lim_{h→0} \frac{f(a+h)-f(a)}{h}$$
を満たすとき関数 $f(x)$ は $x=a$ において微分可能であると言う。このとき上式を $x=a$ における $f(x)$ の微分係数と言い、これを $f'(a)$ と表す。更に上式の $a$ に対して微分係数 $f'(a)$ を対応させる関数
$$\lim_{h→0} \frac{f(x+h)-f(x)}{h}$$
のことを導関数と言い、これを $f'(x)$ と表す。
微分の定義から関数 $f(x)$ の導関数 $f'(x)$ は
$$f'(x)=\lim_{h→0} \frac{f(x+h)-f(x)}{h} \tag{1}$$
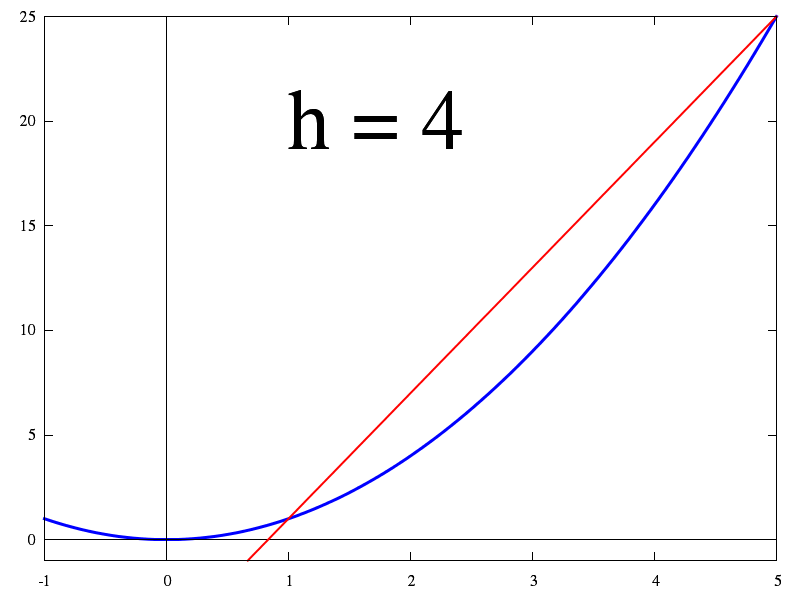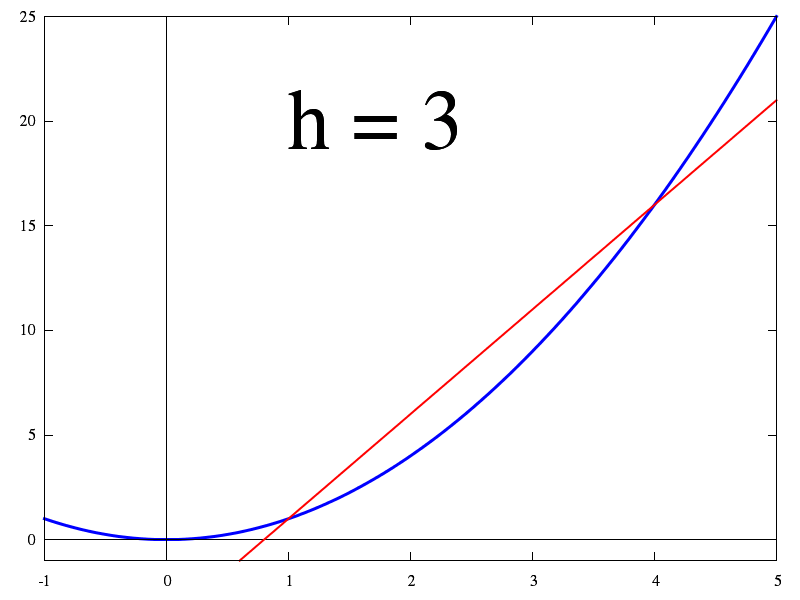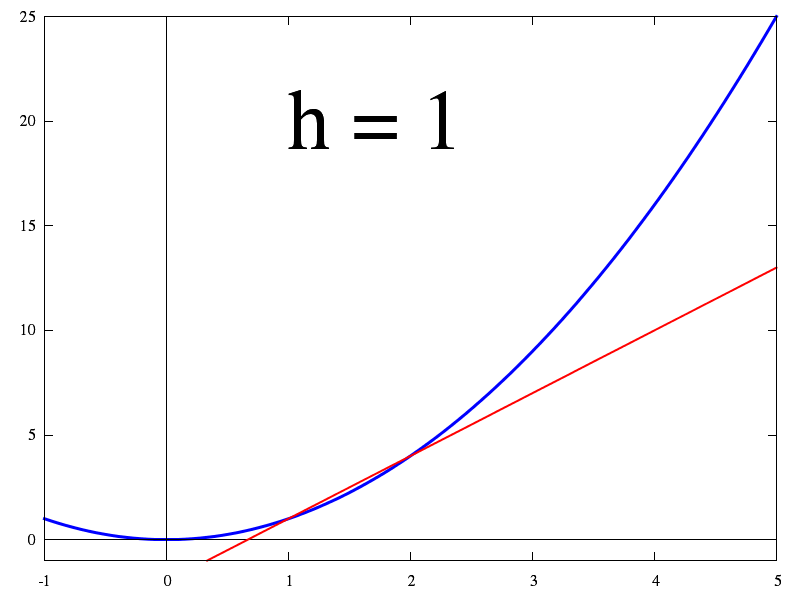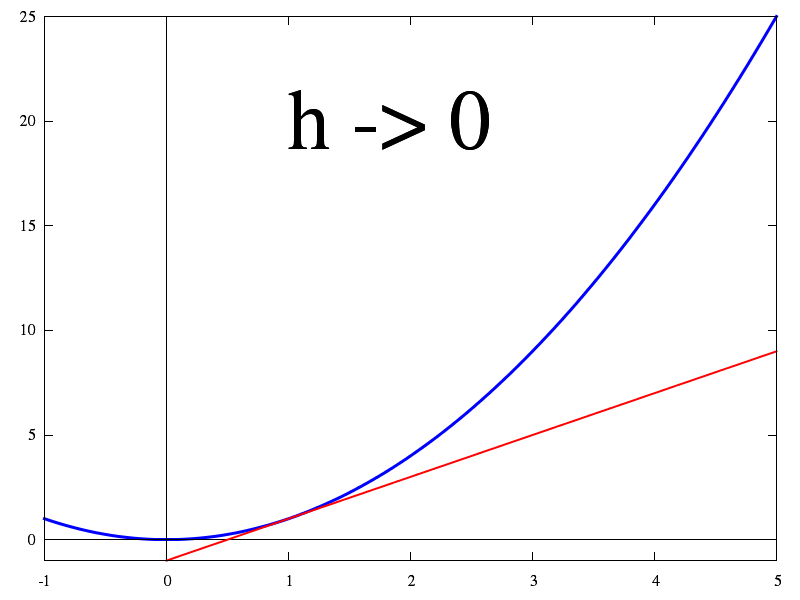
と表されるから、 $h$ が十分に小さいときには
$$f(x+h)-f(x)≈hf'(x)$$
$$∴f(x+h)≈f(x)+hf'(x) \tag{2a}$$
となる。この両辺を $x$ で微分すると
$$∴ f'(x+h)≈\lim_{h→0} \frac{(f(x+h)+hf'(x+h))-(f(x)+hf'(x))}{h}$$
$$∴ f'(x+h)≈\lim_{h→0} \left\{\frac{(f(x+h)-f(x))}{h} +\frac{h(f'(x+h)+f'(x))}{h} \right\}$$
$$∴ f'(x+h)≈f'(x)+hf^{\prime\prime}(x) \tag{3a}$$
以降hを消去するために(2a),(3a)式を
$$f(x)≈f(a)+(x-a)f'(a) \tag{2b}$$
$$f'(x)≈f'(a)+(x-a)f^{\prime\prime}(a) \tag{3b}$$
と置く。
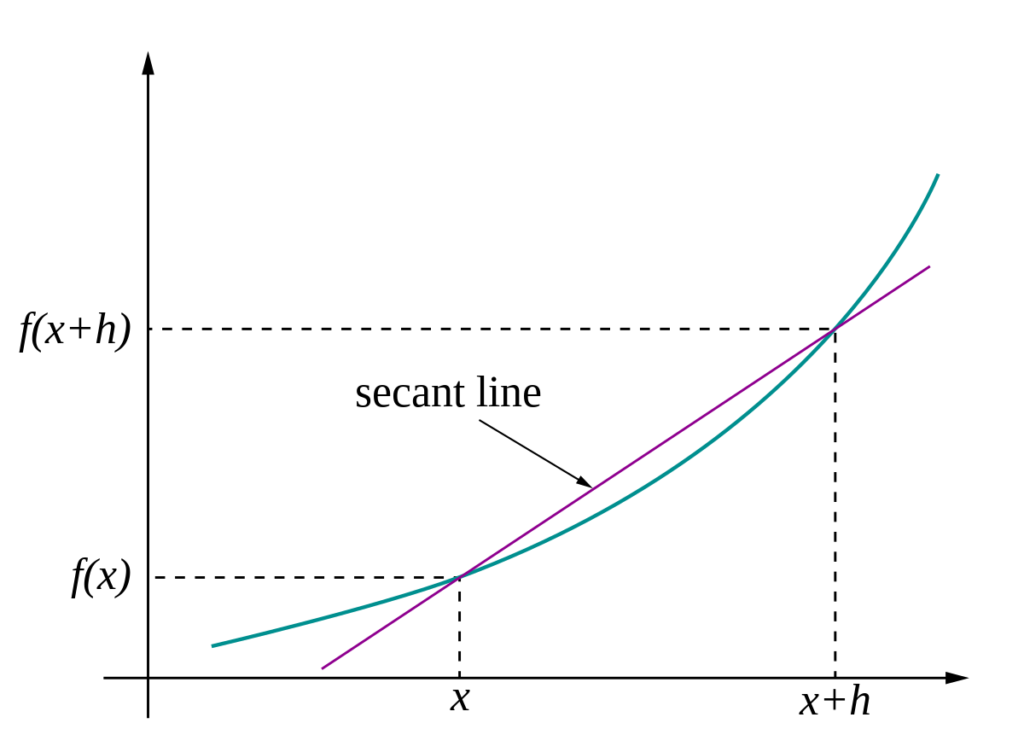
出典:Wiki
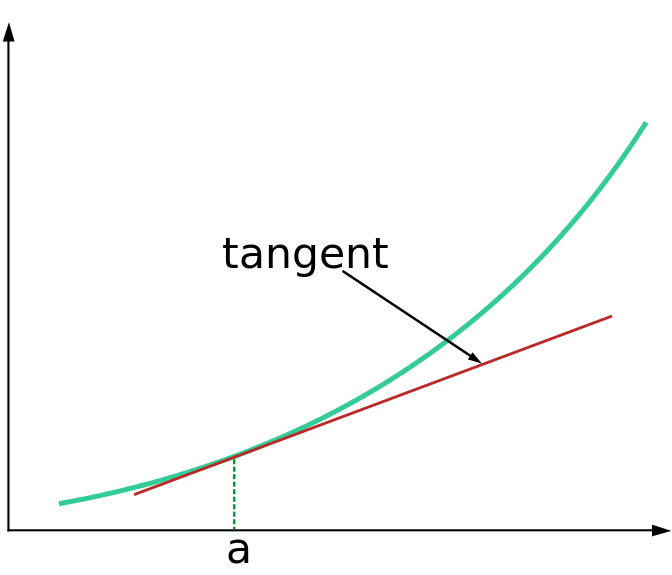
出典:Wiki
出典:Wiki
よって(3b)の両辺を $x$ で積分し、積分定数から適当な定数を指定すると
$$f(x)≈f(a)+(x-a)f'(a)+\frac{1}{2} (x-a)^2f^{\prime\prime}(a) \tag{4}$$
が得られる。もう一度得られた近似式を並べると
$$\begin{cases}
f(x)≈f(a)+(x-a)f'(a) \\
f(x)≈f(a)+(x-a)f'(a)+\frac{1}{2} (x-a)^2f^{\prime\prime}(a)
\end{cases}$$
となり、これまでの計算から $n$ 次近似曲線由来の項は
$$\frac{1}{n!} (x-a)^n\lim_{x-a→0} \left.\frac{f^{(n-1)}(x)-f^{(n-1)}(a)}{x-a} \right|_{x=a}=\frac{1}{n!} f^{(n)}(a)(x-a)^n \tag{5}$$
となる。
よって関数 $f(x)$ を
$$f(x)=\sum_{n=0}^k \frac{1}{n!} f^{(n)}(a)(x-a)^n \tag{6}$$
のように冪級数展開して近似することができる。なおこの近似は区間内の点 $x=a$ 近傍でその妥当性が保証され、 $k$ が大きくなればその近似が妥当であると言える範囲は広がり、やがて微分可能な回数の上限に達するとその近似は与えられた関数 $f(x)$ と一致する。
出典:Wiki
これを拡張したもので三角関数や指数関数等の無限微分可能の場合には関数 $f(x)$ は
$$f(x)=\sum_{n=0}^∞ \frac{1}{n!} f^{(n)}(a)(x-a)^n\tag{7}$$
となる。これをテイラー展開と言い、特に $a=0$ のときにはマクローリン展開と言う。
マクローリン展開を用いた表現
後は各関数をマクローリン展開すると、
$$e^x=1+\frac{x}{1!} +\frac{x^2}{2!} +\cdots=\sum_{n=0}^∞ \frac{x^n}{n!}$$
$$\cos x=1-\frac{x^2}{2!} +\frac{x^4}{4!} -\cdots=\sum_{n=0}^∞ \frac{(-1)^nx^{2n}}{(2n)!}
\sin x=\frac{x}{1!} -\frac{x^3}{3!} +\cdots=\sum_{n=0}^∞ \frac{(-1)^nx^{2n+1}}{(2n+1)!}$$
$$\cosh x=1+\frac{x^2}{2!} +\frac{x^4}{4!} +\cdots=\sum_{n=0}^∞ \frac{x^{2n}}{(2n)!}
\sinh x=\frac{x}{1!} +\frac{x^3}{3!} +\cdots=\sum_{n=0}^∞ \frac{x^{2n+1}}{(2n+1)!}$$
となる。
よって虚数単位を $i$ とすると、その周期性から
$$\begin{align*}
e^{ix}=1+i\frac{x}{1!} -\frac{x^2}{2!} -i\frac{x^3}{3!} +\frac{x^4}{4!} +\cdots&=\sum_{n=0}^∞ \frac{(-1)^nx^{2n}}{(2n)!} +i\sum_{n=0}^∞ \frac{(-1)^nx^{2n+1}}{(2n+1)!}\\
&=\cos x+i\sin x
\end{align*} \tag{8}$$
$$\begin{align*}
e^x=1+\frac{x}{1!} +\frac{x^2}{2!} +\frac{x^3}{3!} +\frac{x^4}{4!} +\cdots&=\sum_{n=0}^∞ \frac{x^{2n}}{(2n)!} +\sum_{n=0}^∞ \frac{x^{2n+1}}{(2n+1)!}\\
&=\cosh x+\sinh x
\end{align*} \tag{9}$$
が得られる。
複素指数関数による三角関数、双曲線関数の表現
先述の通り指数関数は以下
$$e^{iθ} =\cosθ+i\sinθ \tag{8}$$
$$e^{θ} =\coshθ+\sinhθ \tag{9}$$
のようにそれぞれ三角関数と双曲線関数との間に関係式がある。そこで2つの連立方程式
$$\begin{cases} e^{iθ} =\cosθ+i\sinθ\\ e^{-iθ} =\cosθ-i\sinθ \end{cases}$$
$$\begin{cases} e^{θ} =\coshθ+\sinhθ\\ e^{-θ} =\coshθ-\sinhθ \end{cases}$$
を解くことで、三角関数、双曲線関数の指数関数表示が可能になるわけだ。実際にこれらを解くと
$$\begin{cases} \cosθ=\frac{e^{iθ}+e^{-iθ}}{2}\\
\sinθ=\frac{e^{iθ}-e^{-iθ}}{2i}
\end{cases} \tag{10}$$
$$\begin{cases} \cosθ=\frac{e^{θ}+e^{-θ}}{2}\\
\sinθ=\frac{e^{θ}-e^{-θ}}{2} \end{cases} \tag{11}$$
となる。またこれらから三角関数と双曲線関数について以下の関係式
$$\begin{cases}
\cos ix=\cosh x\\
\sin ix=i\sinh x
\end{cases} \tag{12}$$
が導かれる。
ちょっと休憩
本記事では三角関数と双曲線関数を複素指数関数で表現してみた。そのためにテイラー展開の導出や2次近似式の導出もしている。次の記事では逆三角関数と逆双曲線関数について解説しているので意欲のある読者は是非覗いてみてほしい。
逆三角関数、逆双曲線関数はこちら



コメント