本記事はシリーズ「ルジャンドル変換の多角的な理解」の第2部になります。第2部では第1部で考えた接線からルジャンドル変換を解釈していきます。
前回
前書き
本記事ではルジャンドル変換という数学的な概念について解説しています。図形的にはルジャンドル変換とはある滑らかな凸関数の接線の傾きを新たな変数として、その関数を別の関数に変換する操作です。ルジャンドル変換には以下のような性質や応用があります。
- ルジャンドル変換を2回施すと、元の関数に戻る
- ルジャンドル変換は、多変数関数にも適用できる。
この記事では、ルジャンドル変換の定義や求め方、$sup$ と $max$ の違い、微分係数が不連続な場合の扱いなどについて詳しく説明します。なおルジャンドル変換は滑らかな関数でなくても適用されますが、本記事では考える関数は滑らかであるものとします(そうしないとつまらないので)。
ルジャンドル変換の定義と例外
関数 $f(x)$ のルジャンドル変換 $f^*(x)$ の定義は以下のように表される。
凸関数 $f(x)$ についてルジャンドル変換 $f^*(x)$ は以下のように定義される。
$$f^*(p)≡\sup_x(px-f(x))\tag{8}$$
または
$$\begin{align*}&f^*(p)≡px-f(x)\\ &\quad at\ x\ such\ that\ f'(x-0)≤p≤f'(x+0)\end{align*}\tag{6}$$
ルジャンドル変換
(8)式は(7)式と類似しているが違う点は $\max$ か $\sup$ かである。前者は最大値を表現しているが後者は上限を表現している。最大値 $c$ が存在するのなら上限は $c$ となるが、上限が $c$ であるからと言って最大値 $c$ が存在するわけではないことに注意されたい。
参考文献によっては $\inf$ を用いて定義することもあるが、これは直線 $l$ の線座標系を $(p,f^*(p))$ としているだけに過ぎない。
ルジャンドル変換を求める手順
ここでは簡単に滑らかな凸関数 $f(x)$ のルジャンドル変換 $f^*(p)$ を求める手順を紹介し、次ではこれに再度ルジャンドル変換 $f^{**}(x)$ を施してみる。
図形的に考えればルジャンドル変換 $f^*(p)$ となる $x$ の値は関数 $f(x)$ の接点である。つまりルジャンドル変換
$$f^*(p)≡\sup_x(px-f(x))\tag{8}$$
を満たす $x$ の値は $x$ による微分が $0$ になる点であるから
$$\begin{align*}
f^*(p)&=\dfrac{∂}{∂x}((px-f(x))\\
&=p-\dfrac{∂f(x)}{∂x}=0\\
∴{}p&=\dfrac{∂f(x)}{∂x}=f'(x) \tag{9}
\end{align*}$$
を $x$ について解くことによって決まる。
よって(9)式によりルジャンドル変換における $x$ の変換を $x^*(p)$ と置くと
$$x^*(p)=f’^{-1}(p)$$
と表されるから、ルジャンドル変換は
$$\begin{align*}
f^*(p)&≡\sup_x(px-f(x))\tag{8}\\
&=px^*(p)-f(x^*(p))\tag{10}
\end{align*}$$
と書き表される。
$\sup$ は $\max$ よりも都合が良い
例えば関数 $f(x)$ の右側が $l:y=ax+b$ を漸近線に持ち、右側定義域が $,∞)$ となっているものとする。
このとき $x→∞$ のときに関数 $f(x)$ は直線 $l$ に限りなく近づくが、直線 $l$ に交わることはない。よって $a=f'(x)$ となる $x$ は右側定義域 $,∞)$ に存在しないので $ax-f(x)$ を最大値にとる最大の $x$ も存在しない($f(x)$ については極限は存在する)。
しかし関数 $f(x)$ は見ても分かる通り直線 $l$ に限りなく近づくので、傾き $a$ を満たす直線 $ax-f(x)$ は直線 $l$ を上限に持つ(直線 $l$ よりも右側に行くことはない)。
よってルジャンドル変換の定義
$$f^*(p)≡\sup_x(px-f(x))\tag{8}$$
により $f^*(a)$ が存在することが認められた。
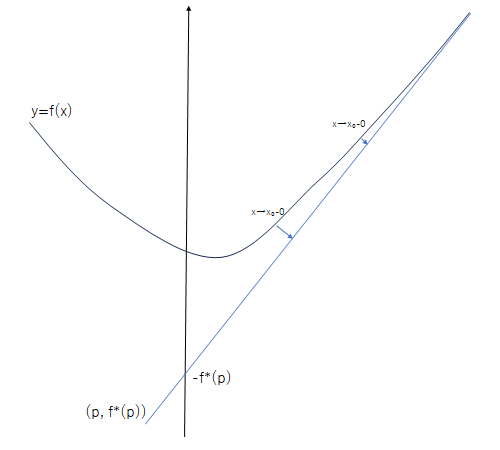
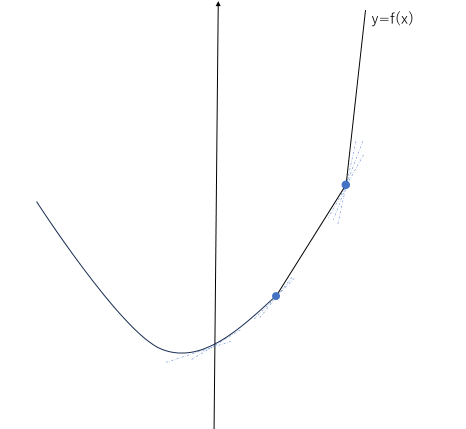
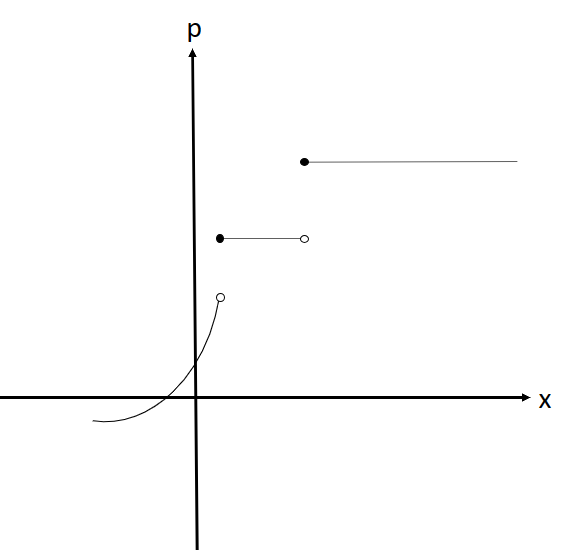
微分係数が不連続である場合
点 $c$ 付近で微分可能である場合(つまり $f'(c-0)=f'(c+0)$)には、傾き $p$ の取る値によって $f^*(p)$ となる $x$ の値は一意に定まらない。逆に微分係数が不連続である場合(つまり $f'(c-0)≠f'(c+0)$)には $x$ の値は微分が不連続な点に複数存在する。
実際に凸関数であれば微分係数 $p$ は $x$ の値が大きくなるにつれ大きくなる。しかし微分係数の左極限と右極限が不連続である場合には、その点 $x$ において右極限に一致するまで潜在的に $p$ の値は増加していると言えよう。
ルジャンドル変換の性質や応用
ルジャンドル変換を2回施すと元の関数に戻る
さてルジャンドル変換を2回施すと
$$\begin{align*}
f^{**}(x)&≡\sup_p(xp-f^*(p))\\
&=xp^*(p)-f^*(p^*(x))\tag{11}
\end{align*}$$
となるので(9)式
$$p=\dfrac{∂f(x)}{∂x}=f'(x) \tag{9}$$
と(10)式
$$f^*(p)=px^*(p)-f(x^*(p))\tag{10}$$
の関係と同様に(9)式と(11)式の関係を比較すると
\begin{cases}
x^*(p)=\left(\dfrac{∂f(x)}{∂x}\right)^{-1}(p)\\
p^*(x)=\left(\dfrac{∂f^*(p)}{∂p}\right)^{-1}(x)
\end{cases}
を得る。(11)式の第2項はルジャンドル変換の形をしているので
$$(11)=xp^*(p)-p^*(x)x^*(p^*(x))-f(x^*(p^*(x)))\tag{12}$$
と変形できる。
ここで
$$\begin{align*}
\dfrac{∂f^*(p)}{∂p}&=x^*(p)+p\dfrac{∂x^*(p)}{∂p}-\dfrac{∂f(x^*(p))}{∂p}\\
&=x^*(p)+p\dfrac{∂x^*(p)}{∂p}-\dfrac{∂x^*(p)}{∂p}\dfrac{∂f(x^*(p))}{∂x^*(p)}\\
&=x^*(p)+p\dfrac{∂x^*(p)}{∂p}-\dfrac{∂x^*(p)}{∂p}p\\
&=x^*(p)
\end{align*}$$
となるから
$$\begin{align*}
p^*(x)=x^{*-1}(p)\\
∴x^*(p^*(x))=x
\end{align*}$$
となり、これを(12)式に代入すれば
$$xp^*(p)-p^*(x)x-f(x)=f(x)$$
となる。よって $f^{**}(x)=f(x)$ が成り立つ。
ルジャンドル変換を2回施すと元の関数に戻ることからルジャンドル変換では元の関数の情報を完全に保っていることが分かる。
多変数関数のルジャンドル変換
今まで1変数 $x$ のルジャンドル変換のみ考えてきたが、当然多変数の場合にも適応することが可能である。例えば $\boldsymbol{r}=(x_0,y_0,z_0),\boldsymbol{a}=(x,y,z)$ として陽関数における接線の方程式
$$l:y=f'(x_0)x-\left(f'(x_0)x_0-f(x_0)\right)\tag{2}$$
を得たときと同じように $\nabla F(\boldsymbol{r}) \cdot (\boldsymbol{a}-\boldsymbol{r})=0$ を計算することで接平面の方程式
$$z=\dfrac{∂f(x_0)}{∂x}x+\dfrac{∂f(y_0)}{∂y}y-\left(\dfrac{∂f(x_0)}{∂x}x_0+\dfrac{∂f(x_0)}{∂x}y_0-f(x_0,y_0)\right)$$
を得る。これによりルジャンドル変換は各変数による偏微分を $p_x.p_y$ と置くことで
$$f^*(p_x,p_y)=p_xx+p_yy-f(x,y)$$
と書き表される。
そこでより一般的な場合でのルジャンドル変換を考えていこう。
まず $n$ 変数関数 $f$ において $r$ 個のルジャンドル変換をする変数 $x^i$ とそれ以外を $a^j$ と置くことにする。つまり変数 $x^i$ の偏微分を $p_i$ と置くきルジャンドル変換 $f→f^*$ によって
$$f^*(p_i,a^j)=x^ip_i-f(x^i,a^j) \tag{13}$$
のように座標変換 $(x^i,a^j)→(p_i,a^j)$ を施すことになるのだ。
ルジャンドル変換 $f^*(p)$ は元の関数 $f(x)$ の接線に関する直線族である
滑らかな凸関数 $f(x)$ において接線の方程式 $l$ はルジャンドル変換 $f^*(p)$ を用いて
$$l:y=px-f^*(p) \tag{4}$$
のように書き表される。この方程式は $p$ の値を変化させることで任意の点 $x$ における接線の方程式となる。このことから(4)式は $p$ を媒介変数とする関数 $f(x)$ の接線に関する直線族となる。
よって(4)式の両辺を媒介変数 $p$ によって偏微分した
$$0=x-\dfrac{∂f^*(p)}{∂p} \tag{14}$$
の $p$ を(4)式に代入することで(4)式の包絡線を得る。この包絡線とは元の関数 $f(x)$ である。
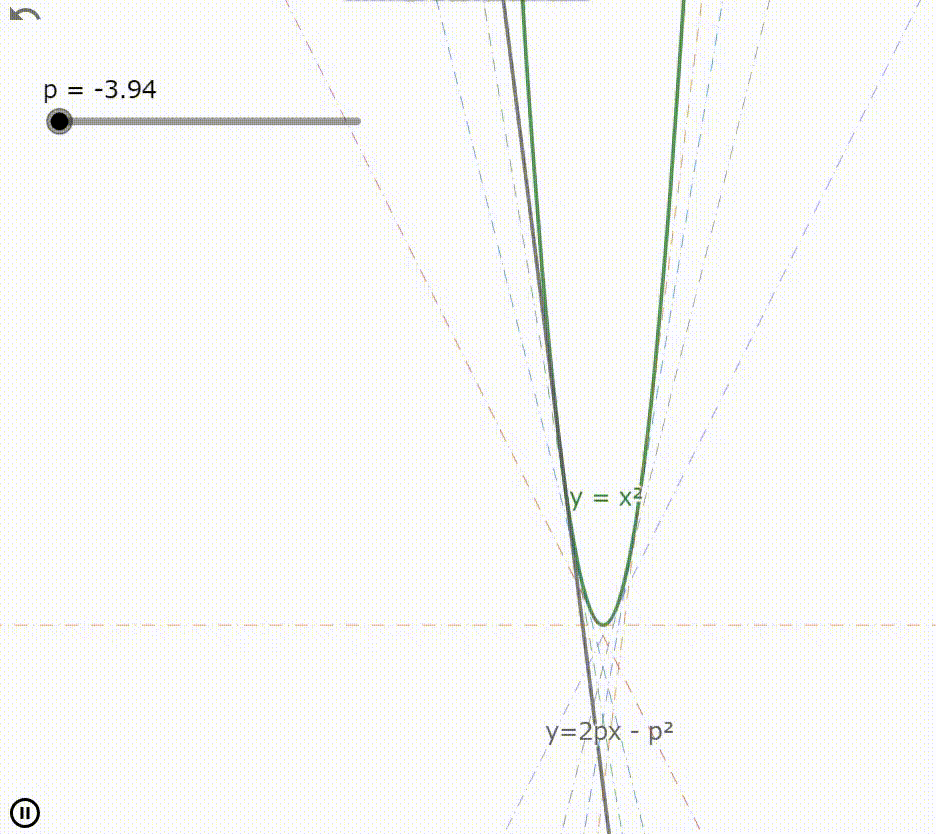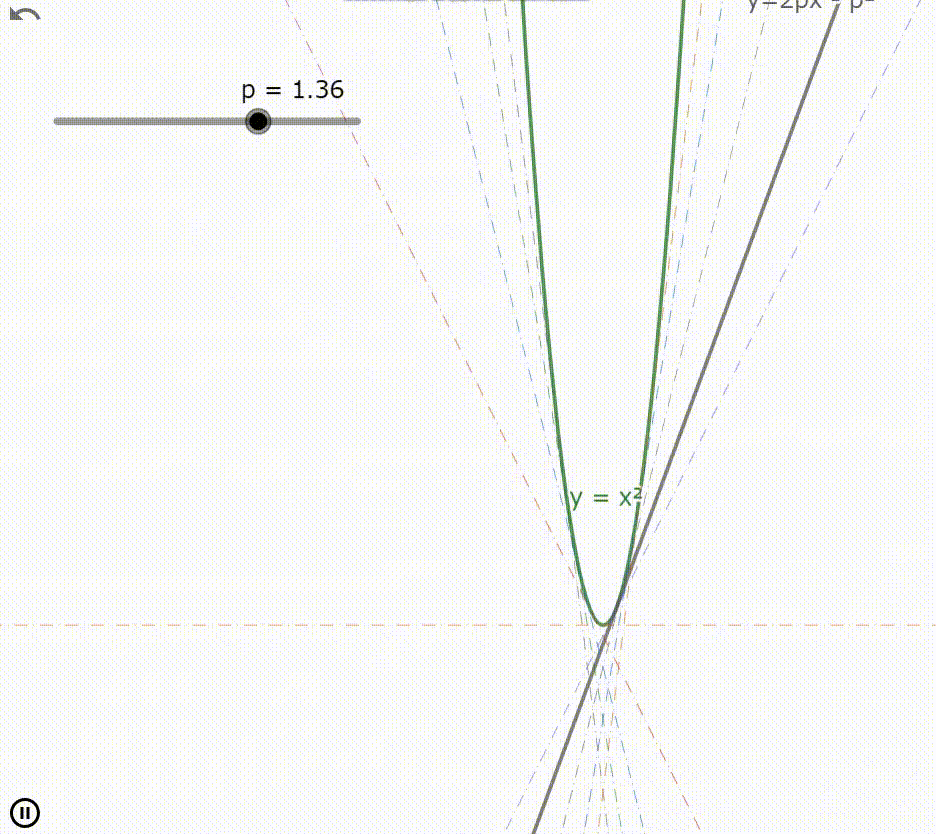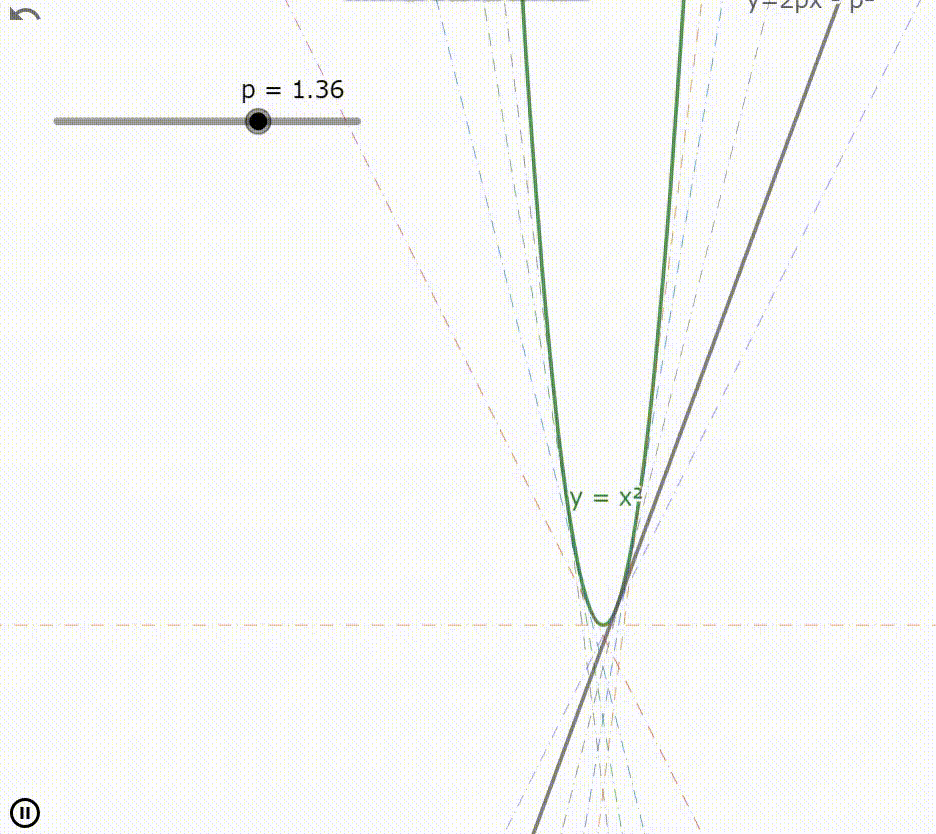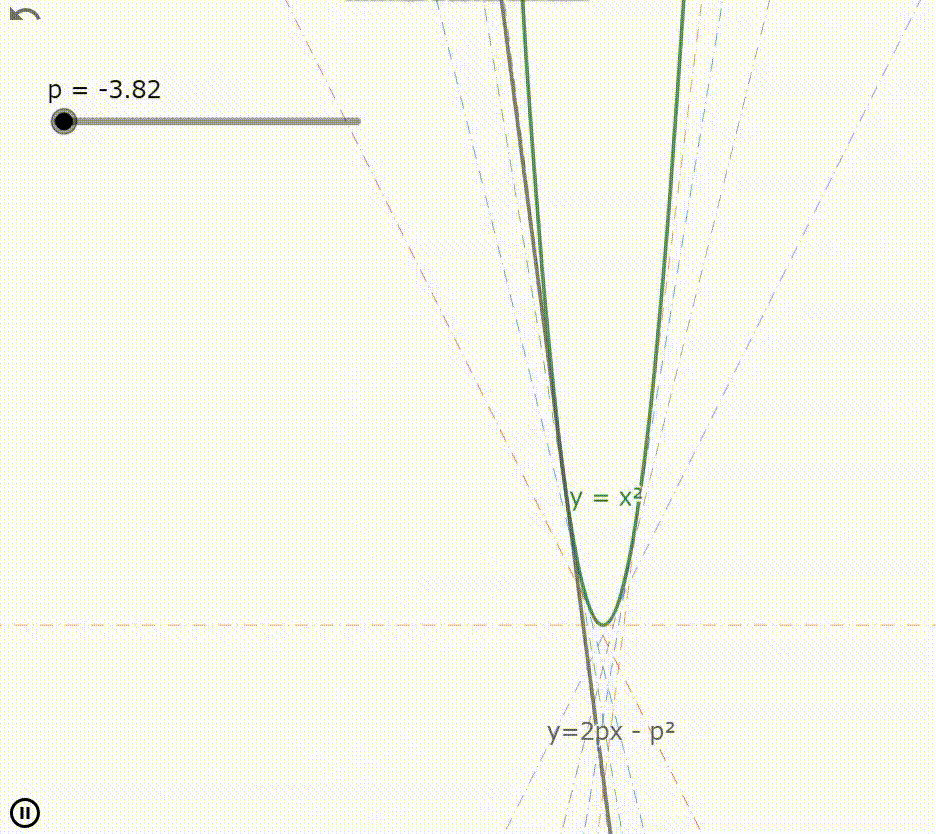
なお今の一連の処理は正しく2回ルジャンドル変換を施したのと本質的には変わらない。
多変数関数の場合には(4)式はルジャンドル変換する数によって接する図形の次元の族になる。例えば2変数にルジャンドル変換を施す場合には接平面の平面族となり、それ以上になればその次元にあった図形になる。
最後に
本記事ではルジャンドル変換を幾何学的に解釈してみた。ルジャンドル変換は物理学でよく見かける手法だが、初学者には敬遠されがちな定義となっている。本記事を読んで色々な応用例に触れてもらえれば幸いである。
前回



コメント