本記事は4部構成のシリーズ「線型演算子 $\hat{A}$ を解析してみた」の第3部となります。
第3部では第1部・第2部で紹介した固有値や射影演算子を用いて、正規演算子の分解をしていきます。
初回
前回
次回
前書き
本記事では線型演算子のスペクトル分解について説明します。スペクトル分解は線型演算子を射影演算子ごとに分解することで、その性質を理解するための重要な手法です。
まず正規演算子のスペクトル分解について考えます。正規演算子はユニタリ演算子によって対角化可能であり、その結果として得られる射影演算子を用いて線型演算子を分解することができます。この分解は直交射影演算子による分解であることから、直交スペクトル分解とも呼ばれます。
次に線型演算子が正規演算子ではない場合、即ち固有空間が非直交である場合のスペクトル分解について考えます。この場合正規直交基底の条件式を満たさないため、線型演算子の分析は少し複雑になります。
スペクトル分解
ここでは線型演算子 $\hat{A}$ を射影演算子 $\hat{P}_i$ ごとに分解することで性質を見ていこう。
正規演算子のスペクトル分解
線型演算子 $\hat{A}$ が正規演算子である場合には、(7)式の通りユニタリ演算子 $\hat{U}$ によって
$$\hat{U}^{*i}_j\hat{A}\hat{U}_i^j=(λ_{ij}δ_{ij})_i^j \tag{7}$$
のように対角化可能である。(7)式の両辺の左から $\hat{U}$ を掛け、右から $\hat{U}^*$ を掛けると、
$$\begin{align*}
\hat{A}&=\hat{U}^{j}_i\hat{U}^{*i}_j\hat{A}\hat{U}_i^j=(λ_{ij}δ_{ij})_i^j\hat{U}^{*j}_{j}\\
&=λ_{ij}\hat{U}_i^j\hat{U}^{*i}_j\\
&=\sum_{i=1}^r\sum_{j=1}^{m_i}λ_{ij}|e_i,j\rangle\langle e_i,j|δ_{ij}\\
&=\sum_{i=1}^rλ_{i}|e_i,m_i\rangle\langle e_i,m_i|\\
&=\sum_{i=1}^rλ_{i}\hat{P}_i ∵(11)
\end{align*}\tag{14}$$
となる。一般に正規演算子 $\hat{A}$を(14)式のように射影演算子 $\hat{P}_i$ ごとに分解することをスペクトル分解と言う。線型演算子 $\hat{A}$ が正規演算子の場合には、部分固有空間 $ν_i$ は直交し、また部分固有空間は基底 $|e_i,m_j\rangle$ による完全正規直交系をとる。このことから直交射影演算子による分解であることを強調して直交スペクトル分解と呼ばれることもある。
実際に線型演算子 $\hat{A}$ に射影演算子 $\hat{P}_i$ を掛けると(14)式は正規直交基底の条件式 $\hat{P}_i\hat{P}_j=\hat{P}_iδ_{ij}$ より
$$\hat{P}_i\hat{A}=λ_i$$
となる。これは他の射影演算子が射影演算子 $\hat{P}_i$ に依存せず、線型演算子 $\hat{A}$ は射影演算子 $\hat{P}_i$ による固有の値 $λ_i$ に依存する。
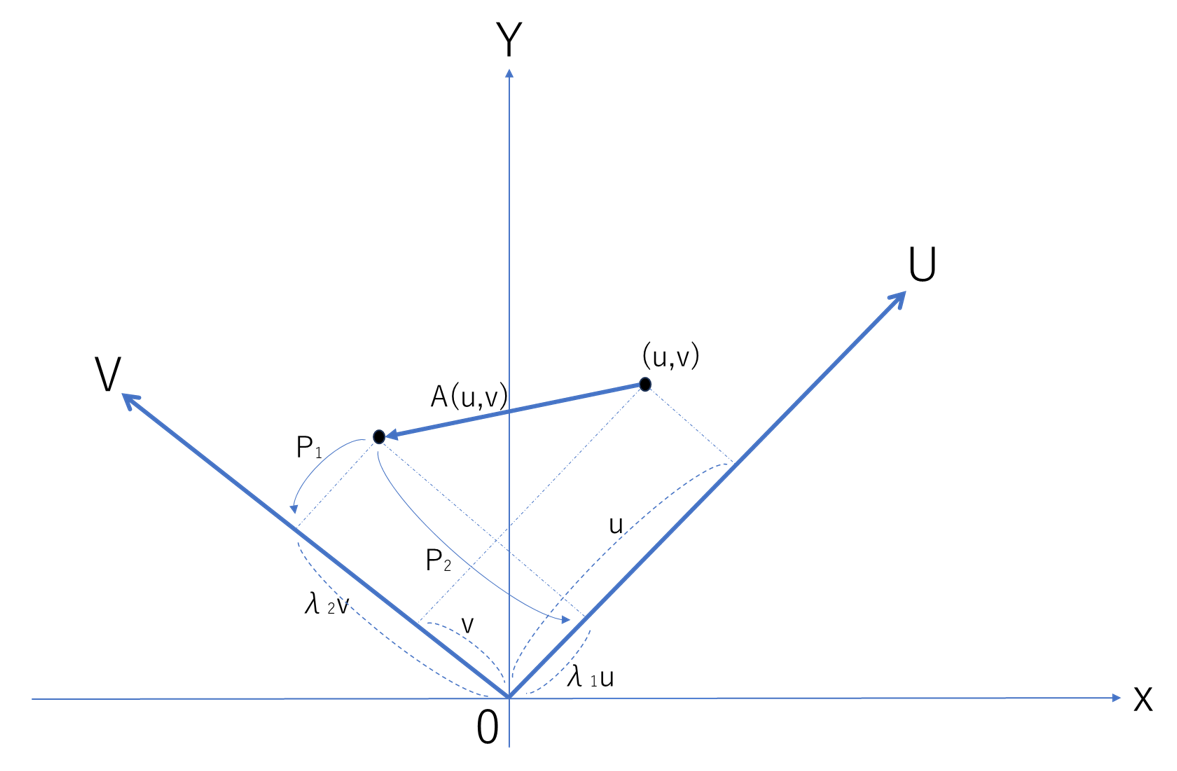
例えば2次正方行列 $A$ を簡単のため2つの射影行列 $P_1,P_2$ によって
$$A=λ_1P_1+λ_2P_2 \tag{15}$$
とスペクトル分解できるとする。ここで射影行列 $P_1,P_2$ がそれぞれベクトル空間 $W$ の部分ベクトル空間 $U,V (W=U\oplus V)$ に属するものとする。このとき(15)式によって各元 $\boldsymbol{u}∈U,\boldsymbol{v}∈V$ としてベクトル $\boldsymbol{x}=\boldsymbol{u}+\boldsymbol{v}$ が線型変換されるとすると、ベクトル $\boldsymbol{x}$ は射影行列 $P_1,P_2$ によって
$$\begin{align*}
A\boldsymbol{x}&=λ_1P_1\boldsymbol{x}+λ_2P_2\boldsymbol{x}\\
&=λ_1\boldsymbol{u}+λ_2\boldsymbol{v}
\end{align*}$$
のように書き表されるのだ。
固有空間が非直交である場合
演算子が正規直交基底でスペクトル分解できるための必要十分条件は、演算子が正規であることである。
このことの証明についてはここでは省くが、今までの解説を読んでもらった読者なら薄々気付いていることだろう。今までは線型演算子 $\hat{A}$ が正規演算子の場合を考えていたが、ここでは正規でない一般の場合について考えていく。
固有空間が非直交である場合には、正規直交基底の条件式
$$\hat{P}_i\hat{P}_j=\hat{P}_iδ_{ij}$$
を満たさない。
よって線型演算子 $\hat{A}$ が
$$\hat{A}=\sum_{i=1}^rλ_{i}\hat{P}_i$$
のように表現されていたと仮定して、ベクトルがベクトル空間 $U_i$ における各元 $\boldsymbol{u}_i∈U_i$ の線型結合 $\displaystyle\boldsymbol{x}=\sum_{i=1}^n\boldsymbol{u}_i$ で書き表されているとする。このとき、このベクトル $\boldsymbol{x}$ が線型演算子 $\hat{A}$ によって線型変換されるとすると、
$$\begin{align*}
\hat{A}\boldsymbol{x}&=\sum_{i=1}^nλ_{i}\hat{P}_i\boldsymbol{x}\\
&=\sum_{i=1}^nλ_{i}\boldsymbol{u}_i
\end{align*}$$
となるが、実際には $\boldsymbol{u}_i$ は一般に直交しなく、つまりベクトル $\boldsymbol{x}$ を元とするベクトル空間 $W$ が各部分ベクトル空間 $U_i$ の直和で表されるとは限らないのだ。
そこで線型演算子 $\hat{A}$ の性質を見ていくために、ベクトル $\boldsymbol{a}_i$ を用いて、線型演算子 $\hat{A}$ の列を
$$\hat{A}=
\begin{pmatrix}
\boldsymbol{a}_1 && \boldsymbol{a}_2 && \cdots &&\boldsymbol{a}_n
\end{pmatrix}$$
のように置く。このとき演算子 $\hat{R}$ と基底 $|e_i\rangle$ の行ベクトル $\hat{Q}$ によって線型演算子を $\hat{A}=\hat{Q}\hat{R}$ の積で表現することで、各基底ごとに性質を測ることができよう。
この行ベクトル $\hat{Q}$ によって演算子 $\hat{R}$ を上三角行列で表現することで、線型演算子 $\hat{A}$ の性質を知ることが可能になるのだ。次の記事では実際に演算子 $\hat{Q},\hat{R}$ の求め方を紹介する。
初回
前回
次回



コメント