じっくりと慣性モーメントの例題を解いてみよう

この記事は4部構成のシリーズ「回転に関する物理量」の第4部になっています。第4部では実際に慣性モーメントを求める問題を解いていきます。勿論変な公式を使わずに丁寧に……。

慣性モーメントと慣性モーメントテンソル

例　原点を中心とする楕円体の慣性モーメント（$z$ 軸周り）

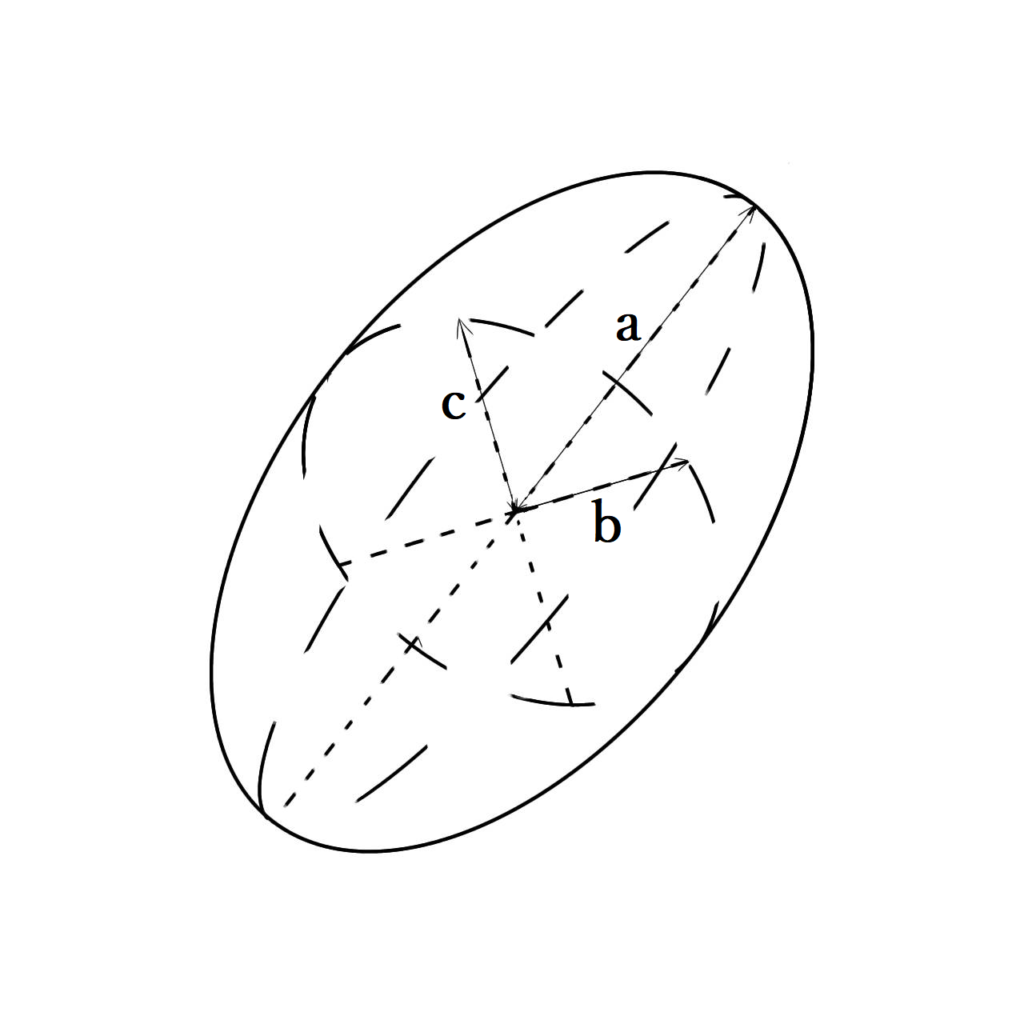
$$\begin{cases}
x=a\sinθ\cosφ\\
y=b\sinθ\sinφ\\
z=c\cosθ
\end{cases}　　(0≤θ≤π,0≤φ≤2π,a,b,c≥0) \tag{23}$$

と表される。これでも良いのだが、より簡素化するために $u=\dfrac{x}{a},v=\dfrac{y}{b},w=\dfrac{z}{c}$ と置くと、(23)式は

$$\begin{cases}
u=r\sinθ\cosφ\\
v=r\sinθ\sinφ\\
w=r\cosθ
\end{cases}　　(0≤θ≤π,0≤φ≤2π,r=1) \tag{24}$$

となり、球座標系 $(r,θ,φ)$ で議論することができる。このとき(22)式は

$$u^2+v^2+w^2=r^2 \tag{25}$$

となる。

さて題意の楕円体の慣性モーメントテンソルを求めたい。そこで単に計算しても良いが、デカルト座標系の基底 $\langle\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3\rangle$ において題意の楕円体は対称であることから、物理学的な観点からもどの座標系の基底を回転軸の向きにとっても回転軸はブレないことが分かる。よって慣性乗積は全て $0$ である。結局求める慣性モーメントテンソルは

$$\boldsymbol{I}=∫_V
ρ(\boldsymbol{r})\begin{pmatrix}
y^2+z^2 & 0 & 0\\
0 & z^2+x^2 & 0\\
0 & 0 & x^2+y^2
\end{pmatrix}d^3r \tag{26}$$

となる。よって題意の楕円体が $z$ 軸を回転軸とする回転をするならば、角運動量 $\boldsymbol{L}$ は

$$\boldsymbol{L}=\boldsymbol{I}ω\boldsymbol{e}_3$$

$$∴ \boldsymbol{L}=∫_Vρ(\boldsymbol{r})(x^2+y^2)\hspace{1mm}d^3r\hspace{1mm}ω\boldsymbol{e}_3 \tag{27}$$

となり、 $z$ 軸周りの慣性モーメント $I$ は

$$I=∫_Vρ(\boldsymbol{r})(x^2+y^2)\hspace{1mm}d^3r \tag{28}$$

を計算すれば良い。ここで題意の楕円体の質量が一様であると仮定すれば、(28)式は

$$(28)=ρ∫_V(x^2+y^2)d^3r=\frac{M}{V}\iiint_V(x^2+y^2)\hspace{1mm}dxdydz \tag{29}$$

となる。ただし題意の楕円体の体積を $V$ と置き、質量を $M$ とした。

次に $x,y,z$ を(23)式

$$\begin{cases}
x=a\sinθ\cosφ\\
y=b\sinθ\sinφ\\
z=c\cosθ
\end{cases} \tag{23}$$

から(24)式

$$\begin{cases}
u=r\sinθ\cosφ\\
v=r\sinθ\sinφ\\
w=r\cosθ
\end{cases} \tag{24}$$

へと置換しよう。なお楕円体の体積は後の計算で明らかになる。このとき微小体要素 $dxdydz$ は

$$dx=adu　dy=bdv　dz=cdw$$

より、

$$dxdydz=abc\hspace{1mm}dudvdw$$

となる。更にこれを $dudvdw$ をヤコビ行列式 $|\boldsymbol{J}|$ を用いて $drdθdφ$ に変換すれば良いのだが、まずはヤコビ行列式 $|\boldsymbol{J}|$ について軽く説明する。

今以下のように

$$\begin{pmatrix}
du\\dv\\dw
\end{pmatrix}=
\begin{pmatrix}
\dfrac{∂x}{∂r} & \dfrac{∂x}{∂θ} & \dfrac{∂x}{∂φ}\\
\dfrac{∂y}{∂r} & \dfrac{∂y}{∂θ} & \dfrac{∂y}{∂φ}\\
\dfrac{∂z}{∂r} & \dfrac{∂z}{∂θ} & \dfrac{∂z}{∂φ}\\
\end{pmatrix}
\begin{pmatrix}
dr\\dθ\\dφ
\end{pmatrix}$$

$$=\begin{pmatrix}
\sinθ\cosφ & r\cosθ\cosφ & -r\sinθ\sinφ\\
\sinθ\sinφ & r\cosθ\sinφ & r\sinθ\cosφ\\
\cosθ & -r\sinθ & 0
\end{pmatrix}
\begin{pmatrix}
dr\\dθ\\dφ
\end{pmatrix} \tag{30}$$

と表される。ここでヤコビ行列 $\boldsymbol{J}$ を

$$\boldsymbol{J}=
\begin{pmatrix}
\sinθ\cosφ & r\cosθ\cosφ & -r\sinθ\sinφ\\
\sinθ\sinφ & r\cosθ\sinφ & r\sinθ\cosφ\\
\cosθ & -r\sinθ & 0
\end{pmatrix}$$

と置くと、(30)式は

$$\begin{pmatrix}
du\\dv\\dw
\end{pmatrix}=
\boldsymbol{J}\begin{pmatrix}
dr\\dθ\\dφ
\end{pmatrix}$$

となるから、

$$\frac{∂(u,v,w)}{∂(r,θ,φ)}=\boldsymbol{J}$$

よって

$$\left|\frac{∂(u,v,w)}{∂(r,θ,φ)}\right|=|\boldsymbol{J}|=r^2\sinθ \tag{31}$$

最後に出てきたこれがヤコビ行列式 $|\boldsymbol{J}|$ である。よって(31)式から

$$dudvdw=r^2\sinθ\hspace{1mm}drdθdφ$$

$$∴ dxdydz=abcr^2\sinθ\hspace{1mm}drdθdφ$$

となり、これで $x,y,z→u,v,w→r,θ,φ$ へ微小体要素の変換ができた。なお途中に全微分、行列式、偏微分の計算を用いたが、今これらを知らない読者はこんな風に変換されるものだと思ってもらうだけで十分である（大学2年生以上の理系なら自分でできて当たり前になる）。

このとき積分範囲は

変数	下端	→	上端
$r$	$0$	→	$1$
$θ$	$0$	→	$π$
$φ$	$0$	→	$2π$

となるから(29)式は

$$\begin{align*}
\frac{M}{V}\iiint_V(x^2+y^2)\hspace{1mm}dxdydz&=\frac{M}{V}∫_{\small{-\dfrac{1}{2}}}^{\small{\dfrac{1}{2}}}du∫_{\small{-\dfrac{1}{2}}}^{\small{-\dfrac{1}{2}}}dv∫_{\small{-\dfrac{1}{2}}}^{\small{-\dfrac{1}{2}}}dw\hspace{1mm}((au)^2+(bv)^2)\hspace{1mm}abc\\
&=\frac{M}{V}∫_0^1dr∫_0^πdθ∫_0^{2π}dφ\hspace{1mm}((ar\sinθ\cosφ)^2+(br\sinθ\sinφ)^2)abcr^2\sinθ\\
&=\frac{M}{V}abc∫_0^1dr∫_0^πdθ∫_0^{2π}dφ\hspace{1mm}r^4\sin^3θ(a^2\cos^2φ+b^2\sin^2φ)
\end{align*}\tag{32}$$

となり、これを積分すれば良い。よって $r,θ,φ$ が独立変数であることに注意して(32)式を計算すると、

$$\begin{align*}
(32)&=\frac{M}{V}abc∫_0^1r^4\hspace{1mm}dr∫_0^π\sin^3θ\hspace{1mm}dθ∫_0^{2π}(a^2\cos^2φ+b^2\sin^2φ)\hspace{1mm}dφ\\
&=\frac{M}{V}abc∫_0^1r^4\hspace{1mm}dr∫_0^π\sinθ(1-\cos^2θ)\hspace{1mm}dθ∫_0^{2π}\frac{1}{2}(a^2(1+\cos(2φ))+b^2(1-\cos(2φ)))\hspace{1mm}dφ\\
&=\frac{M}{V}abc\left[\frac{1}{5}r^5\right]_0^1\left[-\cosθ+\frac{1}{3}\cos^3θ\right]_0^π\left[\frac{1}{2}\left(a^2(φ+\frac{1}{2}\sin(2φ))+b^2(φ-\frac{1}{2}\sin(2φ))\right)\right]_0^{2π}\\
&=\frac{M}{V}abc\frac{1}{5}\left(\frac{2}{3}-\left(-\frac{2}{3}\right)\right)\frac{1}{2}\left(2π(a^2+b^2)\right)\\
&=\frac{1}{5}\frac{M}{V}\frac{4}{3}πabc(a^2+b^2)
\end{align*}\tag{33}$$

となる。ここで楕円体の体積 $V$ とは

$$\begin{align*}
V=∫_Vd^3r=\iiint_Vdxdydz&=\iiint_Vabcr^2\sinθ\hspace{1mm}drdθdφ\\
&=∫_0^1dr∫_0^πdθ∫_0^{2π}dφ\hspace{1mm}abcr^2\sinθ=\frac{4}{3}πabc
\end{align*}$$

であることから $z$ 軸周りの慣性モーメント $I_z$ は

$$I_z=(33)=\frac{1}{5}M(a^2+b^2)$$

となる。よって他の慣性モーメントテンソルの要素はこれの変数を入れ替えれば良く、題意の楕円体における慣性モーメントテンソル $\boldsymbol{I}$ は

$$\boldsymbol{I}=
\begin{pmatrix}
\dfrac{1}{5}M(a^2+c^2) & 0 & 0\\
0 & \dfrac{1}{5}M(c^2+a^2) & 0\\
0 & 0 & \dfrac{1}{5}M(a^2+b^2)
\end{pmatrix} \tag{34}$$

となる。

途中極座標系の3重積分（体積分）を計算したが、今は分からない読者でも大学2年生の理系なら解けるようになっているので安心してほしい。

最後に

このシリーズ「回転に関する物理量」では剛体における慣性モーメントテンソルの導出をした。工学部や建築学科系の授業では慣性モーメントテンソルについて詳しく解説されず、ただよく分からずに慣性モーメントの公式に則って慣性モーメントだけを求めさせられるみたいである。実際に私も慣性モーメントテンソルを理解していれば出てこないような質問を受けたことがあるが、そのときは慣性モーメントテンソルについて話すことにした。問題を解く上では慣性モーメントテンソルまで求めなくても良いが、慣性モーメントテンソルが分かってしまえばどこの軸周りで対称なのか一目瞭然である。また行列からスカラーへテンソルの階数を落とすことで、線型変換におけるテンソルの振舞い方を知ることができる。そのため初学者には特にテンソルまで求めることをお勧めしているのである。

慣性モーメントテンソルは古典力学の集大成ともいえる分野である。それは慣性モーメントテンソルを確りと勉強するには、相応の数学の知識が必要になるだけでなく他分野との融合問題を作りやすいからである。例えば振り子の運動をさせたり、摩擦のある道を紐で引っ張ったりなど。単に慣性モーメントの公式やエネルギー保存則を立てるだけに留まってしまうのはかなり勿体無いのだ。