初めに
本記事はシリーズ「連立方程式の解から束の考え方を導入してみる」の第2部です。本記事では連立方程式を束の観点から見てみると共に、線座標系を定義していこうと思います。中学数学で習った連立方程式は単に計算させるだけで、得られる解はデカルト座標系においては図形の交点を表すことしか伝えられません。本記事では連立方程式から射影幾何学における束という考え方を紹介し、そこから線について新たに線座標系を導入することで解説していきます。
前回
直線束から連立方程式を見てみる
連立一次方程式の解と交点
今までは連立方程式を解くために各方程式を簡潔にしてきた。どんな方法で解いたとしても、結局は各方程式に含まれる変数を消去するという操作を施すことになる。そこで再度連立方程式
{x+y=52x−y=1
を解いてみる。しかしただ解くというわけではなく、連立方程式(1)式を(5)式のように置いて考える。
λ(x+y−5)+μ(2x−y−1)=0
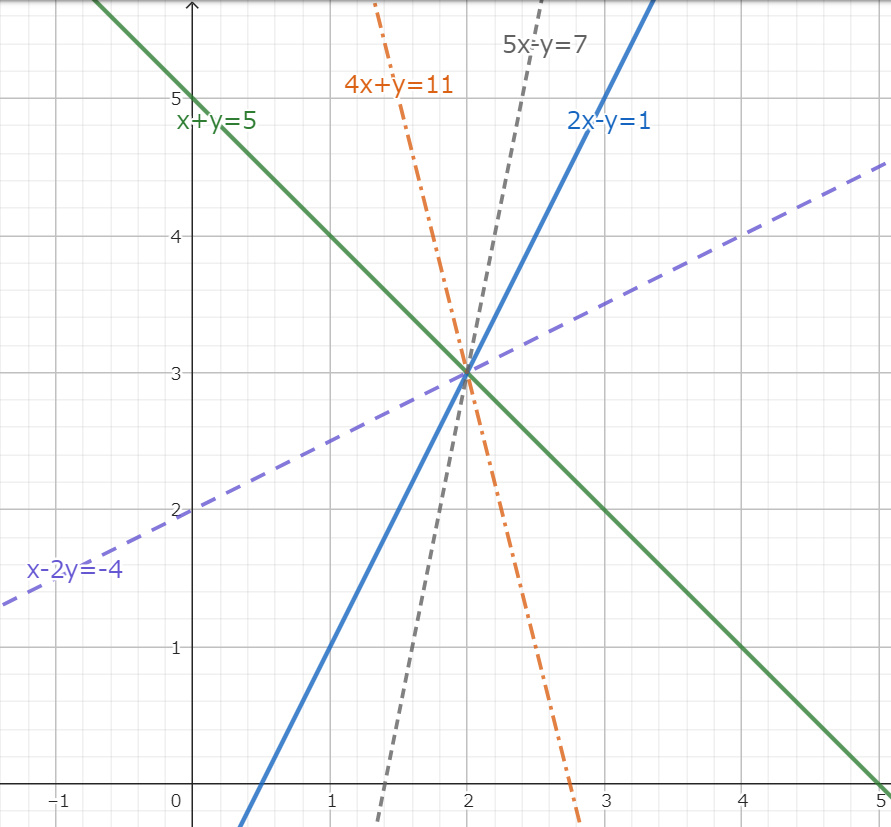
このとき [λ:μ=1:1] のときに解 x=2 が得られ、 [λ:μ=−2:1] のときに解 y=3 が得られるという仕組みである。もう少し詳しく見るために幾つか λ,μ の比を定めてみよう。
[λ:μ=2:1]⇒4x+y=11[λ:μ=−1:1]⇒x−2y=−4[λ:μ=12:1]⇒5x−y=7
右図を見ると(5)式を満たす直線は全て連立方程式(1)式の解 (2,3) を通過することが分かる。
この考え方は多元一次連立方程式の場合にも応用される。例えば連立方程式(3)式
{3x2+3x3−2x4=−4x1+x2+2x3+3x4=2x1+2x2+3x3+2x4=1x1+3x2+4x3+2x4=−1
については
λ1(x2+3x3−2x4+4)+λ2(x1+x2+2x3+3x4−2)+λ3(x1+2x2+3x3+2x4−1)+λ4(x1+3x2+4x3+2x4+1)=0
を満たす [λ1:λ2:λ3:λ4] の組は一意に依らず
(x1x2x3x4)=(7−20−1)+α(−1−110)
を通過する図形となる。
具体的に
[λ1:λ2:λ3:λ4=1:2:3:4]⇒9x+23y+32z+18w=−1[λ1:λ2:λ3:λ4=3:2:1:4]⇒7x+25y+29z+10w=−11[λ1:λ2:λ3:λ4=2:3:4:1]⇒8x+20y+28z+15w=1[λ1:λ2:λ3:λ4=3:4:2:1]⇒7x+20y+15z+12w=−3
のときには4次元デカルト座標系 (x1,x2,x3,x4) において、これら4つの方程式によって得られる解は定点 (7,−2,0,−1) を交点とする。
束という考え方
このように特定の点を通る線を成す族を幾何学的に解釈したものを束と言う。ここでは直線束を考えているが、例えば原点を中心とする半径 2 の円と、点 (1,2) を中心とする半径 3 円の交点を通過する図形は
λ(x2+y2−4)+μ((x−1)2+(y−2)2−9)=0
のように表現できる。ここでも [λ:μ] の比率は無数に存在する。
一般に n 次元座標空間で方程式 C1,C2,⋯,Cn=0(Ciはn変数関数) で表される曲線の共有部分における図形を求めるためには、幾つか式が必要である。連立方程式であれば、連立方程式の解が存在するということは、共通の共有部分を全ての式が満たしているということである。
ここで一般に n 元連立方程式が r 個の方程式 C1,C2,⋯,Cn=0 で表現されていて、かつ全ての方程式が同一の解を含む場合には、 n 次元デカルト座標系においてこれらの方程式で表される共通な共有部分を通過する図形は
λ1C1+λ2C2+⋯+λrCr=0
のように書き表される。ここで r と n の大きさに大小関係を定めていないことに注意されたい。(6)式で表現される束は r 次の束と呼ばれるのだが、次数のように扱われるのはこれらの媒介変数 (λ1,λ2,⋯,λr) が恰も r 次元の座標系のように見做されるからである。
束における媒介変数の正体
線座標系の導入
点の位置を指定するためには座標を用いる。例えば2次元デカルト座標系においては (x,y) と表現したり、円座標系においては (r,θ) と表現したりした。同じように線の位置を指定するために線座標系を導入しよう。
簡単にどういうものかイメージするために例えば直線の方程式について考えてみる。直線の方程式とは
y=ax+b
のように傾き a と y 切片 b によって特徴付けられる。この直線を線座標系で (a,b) と表現することができる。私はこれを陽関数による線座標系(もしくは線座標系の陽表現)と呼んでいる。
動機付けとしてはこれで問題なかろう。しかし一般的には線座標系(3次元の場合)と言えば、
lx+my+n=0
で書き表される線について (l:m:n) とされるものである。こちらは対照的に陰関数による線座標系となっている。例えば各値を (λl:λm:λn) のように λ 倍したところで (右辺)=0 であるから (l:m:n) となる。結局のところ比率が等しい線座標系の場合には同一の直線を表現するのだ。この書き表し方によって (x,y) 平面における任意の線(7)を表現することが可能なのである。また定数項が無いような線、例えば
lx+my+nz=0
の場合には斉次座標系となる。このとき線が原点を通ることから、重心座標系等で議論を円滑に進めるために広く使われる。平行移動という操作をせずに議論を進められるのである。
線座標系を変数とする関数
関数 z=f(x,y) で利用される変数 x,y,z とは3次元デカルト座標系 (x,y,z) において、平面 (x,y) における各点座標を z の値として数値化していると言える。ここでこの z の値を常に 0 となるように定める、即ち z=f(x,y)=0 となるように方程式を立てるとしよう。このとき方程式 f(x,y)=0 で表現される点座標は (x,y,0) となり、 z=0 もしくは xy 平面上の各点 x,y は陰関数表示された曲線 f(x,y)=0 上の点となる。
この考え方をそっくりそのまま線座標系に適応させてみよう。変数 l,m に依存する関数 n=φ(l,m) が3次元線座標系 (l:m:n) に対応しているものとする。ここで n=φ(l,m)=c となるように方程式を立てると、このとき lm 平面上の各線
lx+my=c
は陰関数表示された曲線 φ(l,m)=c 上の線となる。
点座標系の関係式から線座標系の関係式を導く
(8)式について点座標系の変数 x,y の関係式から線座標系の変数 l,m の関係式を導こう。
接線の方程式の場合
関数 f(x,y) の勾配 ∇f(x,y) は法線ベクトルとなる。よってこの関数 f(x,y) 上のある点 (p,q) における法線ベクトルの1つは
\left.\dfrac{∂f}{∂x}\right|_{(p,q)}\boldsymbol{e}_x+\left.\dfrac{∂f}{∂y}\right|_{(p,q)}\boldsymbol{e}_x \tag{9}
である。これにより接線の方程式は
x\left.\dfrac{∂f}{∂x}\right|_{(p,q)}+y\left.\dfrac{∂f}{∂y}\right|_{(p,q)}=c \tag{10}
となる。はあ?なんだそりゃ。と思ったら以下の記事辺りを参照するように。
この式と(8)式の変数 (x,y) をある点 (p,q) としたもの
lp+mq=c\tag{11}
を比較すると
l=\left.\dfrac{∂f}{∂x}\right|_{(p,q)},\hspace{1mm}m=\left.\dfrac{∂f}{∂y}\right|_{(p,q)} \tag{12}
となっていることが分かる。この(12)式を用いて変数 (x,y)→(l:m) の置換をすることで、関数 f 上の接点 (p,q) における線座標系 (l:m) の関係式が導かれるのである。
例えば (x,y) が半長軸が 3(x軸) ,半短軸が 2(y軸) の楕円
\dfrac{x^2}{9}+\dfrac{y^2}{4}=1
を満たすときには
l=2×\dfrac{p}{4},\hspace{1mm}m=2×\dfrac{q}{9}
となる。このとき(11)式は (p,q) を消去して
\dfrac{l^2}{4}+\dfrac{m^2}{9}=c
となり、z=c における xy 射影平面おいて (l:m) が半長軸が 3(y軸) ,半短軸が 2(x軸) の楕円を満たすのだ。
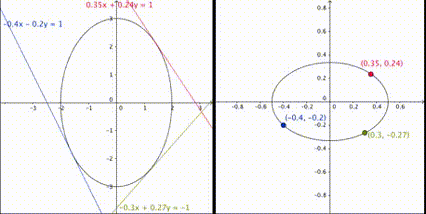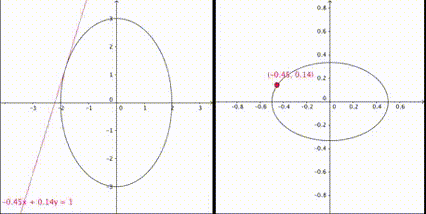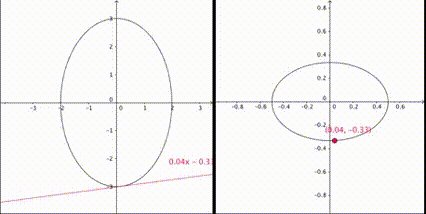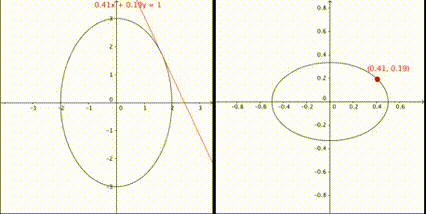
出典:Wiki
2次の接線(曲線)の場合
関数 f_{(x,y)} 上の点 (p,q) における法線ベクトルは
\left.\dfrac{∂f}{∂x}\right|_{(p,q)}\boldsymbol{e}_x+\left.\dfrac{∂f}{∂y}\right|_{(p,q)}\boldsymbol{e}_x \tag{9}
であり、この点 (p,q) による接線の方程式は
x\left.\dfrac{∂f}{∂x}\right|_{(p,q)}+y\left.\dfrac{∂f}{∂y}\right|_{(p,q)}=c \tag{10}
となるのであった。簡単な2次の接線
x^2\left.\dfrac{∂f}{∂x}\right|_{(p,q)}+y^2\left.\dfrac{∂f}{∂y}\right|_{(p,q)}=c \tag{13}
を考えてみよう。2次の接線の場合にも p,q を消去することで線座標系 (l,m) の関係式が導かれる。よってこの式の点 (x,y) を (p,q) としたものと
lp^2+mq^2=c\tag{14}
を比較すれば良い。
具体的に2次曲線
f_{(x,y)}=4x^2+2xy+3y^2-9=0
について、
\begin{align*} \left.\dfrac{∂f}{∂x}\right|_{(p,q)}=8p+2q\\ \left.\dfrac{∂f}{∂y}\right|_{(p,q)}=2p+6q \end{align*}
となり、これと(11)式の係数を比較して
\begin{align*} l=8p+2q\\ m=2p+6q \end{align*}
となる。これを p,q について解いたものを(14)式に代入すると
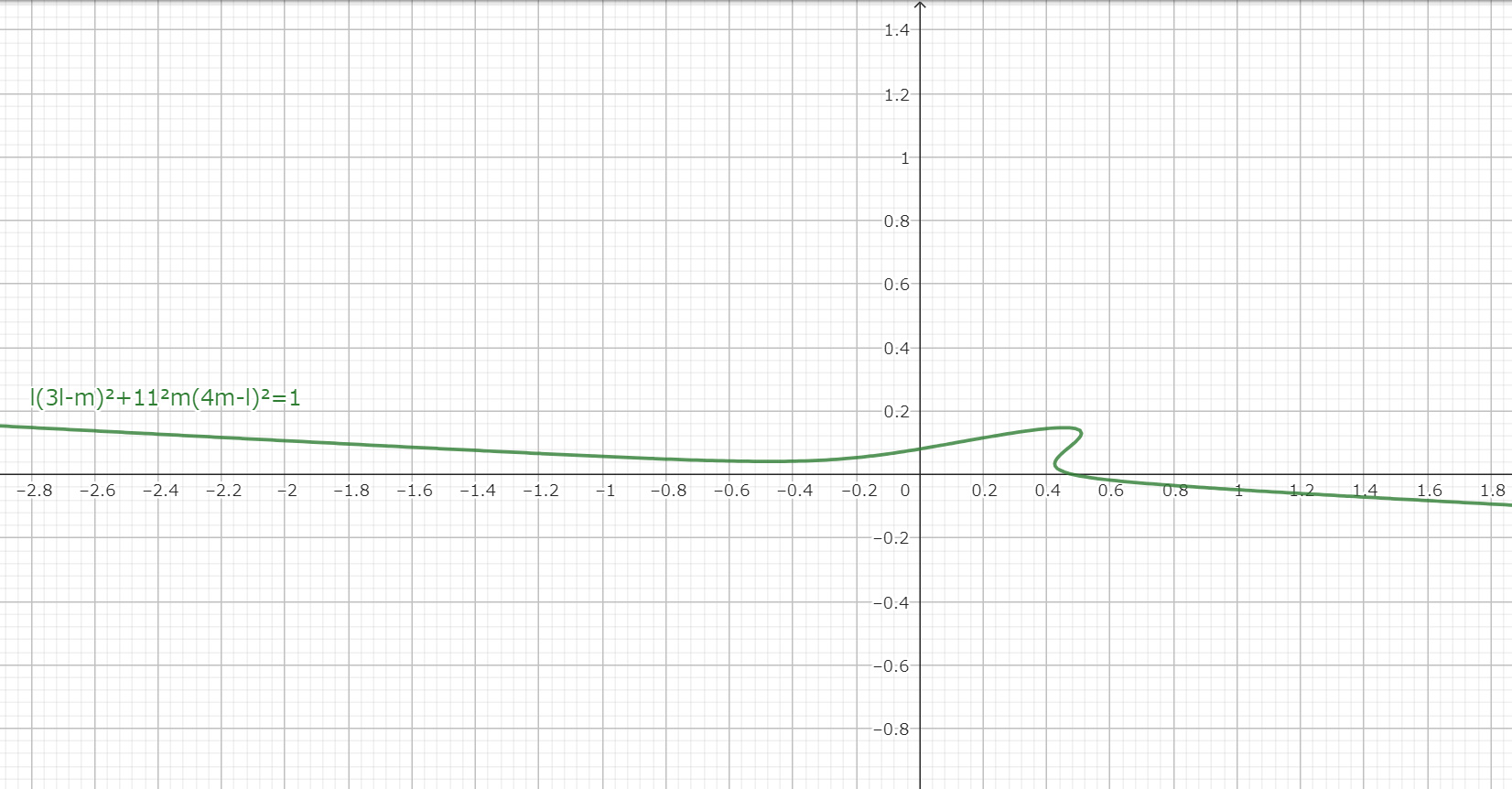
l(3l-m)^2+11^2m(4m-l)^2=22^2c
となる。これが z=22^2c における xy 射影平面において線座標系 (l:m) が満たすべき曲線である。なお一応(11)式の係数を置き換えた
(8p+2p)(x^2-p)+(2p+6q)(y^2-q)=0
について、例えば (p,q)=(1,1) のとき、
10 (x^2-1)+8 (y^2-1)=0
は曲線 4x^2+2xy+3y^2-9=0 上の点 (1,1) で接する2次の接線となる。
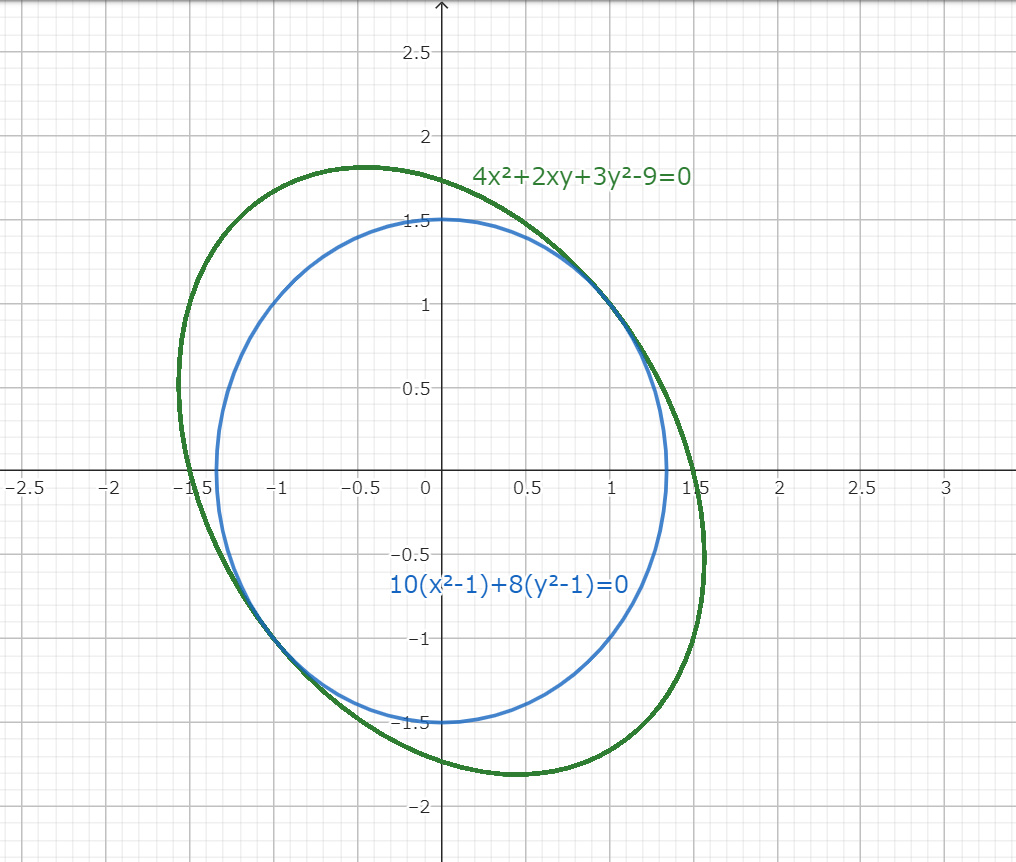
なおここで示した2次の接線は一例にしか過ぎない。偏微分係数 (\left.\dfrac{∂f}{∂x}\right|_{(p,q)},\left.\dfrac{∂f}{∂x}\right|_{(p,q)}) が等しいような2次曲線であれば点 (p,q) で接し、その数は無数に存在するのである。
終わりに
本シリーズを通して連立方程式と束の関係性、及び線座標系を紹介してきた。これらは射影幾何学の内容であり、大学でも学ぶことはあまりないかもしれない。なんせWikiには日本語版の線座標系や斉次座標系の説明がないのである。かなり端折って説明しているので、詳しく勉強したい読者は頑張って参考文献を探してほしい。チェバの定理やメネラウスの定理辺りを漁れば多分あるかもしれない。
前回



コメント